FTF 5 semestr.PROHOROV / Лекции / лекции_1-ядро

I. ФИЗИКА АТОМНОГО ЯДРА

1. Размер, состав и заряд атомного ядра. Массовое и зарядовое числа

Э.Резерфорд, исследуя прохождение -частиц с энергией в несколько мегаэлектрон-вольт через тонкие пленки золота, пришел к выводу о том, что атом состоит из положительно заряженного ядра и окружающих его электронов. Проанализировав эти опыты, Резерфорд также показал, что атомные ядра имеют размеры примерно 10–14 – 10–15 м (линейные размеры атома примерно 10–10 м).

Атомное ядро – положительно заряженная центральная часть атома, в которой сосредоточена практически вся масса атома. Все атомные ядра (кроме ядра атома водорода) состоят из элементарных частиц – протонов и нейтронов. Протонно-нейтронная модель ядра была предложена в 1932 г. Д.Д.Иваненко и В.Гейзенбергом. Протоны и нейтроны называют нуклонами. Нуклоны в ядре удерживаются ядерными силами и движутся внутри ядра с нерелятивистскими скоростями. Наряду с термином «атомное ядро» используется также название нуклид (общее название атомных ядер, отличающихся числом протонов Z и нейтронов N).

Протон (р) – положительно заряженная частица с зарядом, равным элементарному заряду е, и массой покоя тp = 1.6726485∙10-27 кг 1836me (me – масса электрона).

Нейтрон (п) – нейтральная частица с массой покоя mn = 1.6749543∙10–27 кг 1839me. Протоны и нейтроны являются фермионами и имеют спин ħ/2.

Атомные ядра характеризуются зарядовым числом Z: оно равно числу протонов в ядре, совпадает с порядковым номером химического элемента в Периодической системе элементов Менделеева и определяет заряд ядра +Ze. Общее число нуклонов в атомном ядре называют массовым числом А. Таким образом, разность чисел N = A – Z определяет число нейтронов в ядре. Нуклонам (протону и нейтрону) приписывается А = 1, электрону А = 0.

Для обозначения ядер используется символическая запись ZAX , где Х – символ химического элемента, Z – атомный номер (число протонов в ядре), А

– массовое число (число нуклонов в ядре), например 2713Al, 23892U и т.д. Атомные ядра одного и того же элемента с различным числом ней-

тронов называют изотопами. Изотопы имеют одинаковое число Z (одинаковое число протонов) и различные массовые числа А (различное число нуклонов), например 11H, 21H, 31H.

Атомные ядра различных элементов с одинаковым массовым числом

1

А называют изобарами: изобары имеют различные Z (различное число протонов) и одинаковое массовое число (одинаковое число нуклонов), напри-

мер 104Be, 103B, 104C.

Атомные ядра различных элементов с одинаковым числом нейтронов N (N = A – Z) называют изотонами: изотоны имеют различные Z (различное число протонов), различное массовое число А (различное число нуклонов), но одинаковое N (одинаковое число нейтронов), например 146C, 157 N, 168O.

Так как атом нейтрален, то заряд ядра определяет и число электронов в атоме. От числа же электронов зависит их распределение по состояниям в атоме, от которого, в свою очередь, зависят химические свойства атома. Следовательно, заряд ядра определяет специфику химического элемента, т. е. число электронов в атоме, конфигурацию их электронных оболочек, величину и характер внутриатомного электрического поля.

Форму атомных ядер в первом приближении можно считать сферической. Опыты по рассеянию заряженных частиц на ядрах приводят к выводу, что радиус ядра может быть выражен следующей эмпирической формулой:

где R0 = l.3 l.7 фм = (1,3 1,7)∙10–15 м. Следовательно, объем ядра пропорционален числу нуклонов в ядре, а средняя плотность числа нуклонов в ядре (их число в единице объема) для всех многонуклонных ядер практически одинакова: 1017 кг/м3.

2. Дефект массы и энергия связи ядра

Исследования показывают, что атомные ядра являются устойчивыми образованиями. Это означает, что в ядре между нуклонами существует определенная связь.

Массу ядер очень точно можно определить с помощью массспектрометров – измерительных приборов, разделяющих с помощью электрических и магнитных полей пучки заряженных частиц (обычно ионов) с разными удельными зарядами Q/m. Масс-спектрометрические измерения показали, что масса атомного ядра меньше суммы масс составляющих его нуклонов.

Для объяснения этого результата следует вспомнить, что сформули-

рованная Эйнштейном эквивалентность массы и энергии утверждает постоянство полной энергии, а не массы. Поэтому при сближении ну-

клонов на расстояния порядка ядерных возникает энергия связи, появление которой отражается в уменьшении массы атомного ядра. Из закона сохранения энергии вытекает и обратное: для разделения ядра на составные час-

2

ти необходимо затратить такое же количество энергии, которое выделяется при его образовании. Энергия, которую необходимо затратить, чтобы расщепить ядро на отдельные нуклоны, называется энергией связи ядра.

Итак, энергия связи ядра – это энергия, необходимая для расщепления ядра на отдельные нуклоны. Энергия связи нуклонов в ядре

где тр, mn, mя, – соответственно массы протона, нейтрона и ядра. В таблицах обычно приводятся не массы mя, ядер, а массы т атомов. Поэтому для энергии связи ядра пользуются формулой

где mH – масса атома водорода. Так как mH больше тp на величину тe то первый член в квадратных скобках включает в себя массу Z электронов. Но так как масса атома т отличается от массы ядра mя как раз на массу Z электронов, то вычисления по формулам (2) и (3) приводят к одинаковым результатам.

Величину

называют дефектом массы ядра. На эту величину уменьшается масса всех нуклонов при образовании из них атомного ядра.

Удельная энергия связи Eсв = Eсв/A – энергия связи, приходящаяся на один нуклон. Она характеризует устойчивость (прочность) атомных ядер: чем больше Eсв, тем устойчивее ядро.

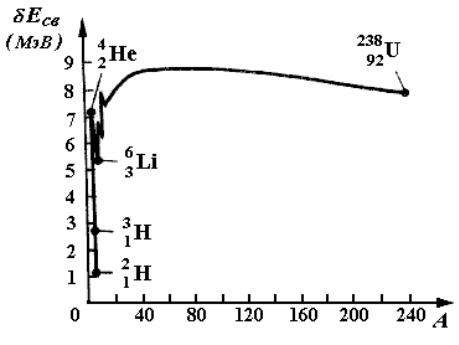
Удельная энергия связи зависит от массового числа А химического элемента (рис. 1). Как следует из рисунка, удельная энергия связи для большинства ядер равна 6 8 МэВ/нуклон. Ее максимум (8,7 МэВ) приходится на область с массовыми числами А = 50 60, что соответствует наиболее стабильным ядрам. По мере увеличения А удельная энергия связи Есв постепенно уменьшается у тяжелых элементов и составляет, например, для 23892U величину 7,6 МэВ/нуклон. Это уменьшение объясняется тем, что с

возрастанием числа протонов в ядре увеличивается и энергия их куло-

новского отталкивания: связь между нуклонами становится менее сильной, в результате чего ядра – менее прочными.

В области малых массовых чисел (А 12), т.е. для легких ядер, удельная энергия связи Есв круто возрастает до 6 7 МэВ, претерпевая целый ряд скачков (например, для 21H Eсв = 1,1 МэВ, для 42He – 7,1 МэВ, для 63Li

– 5,3 МэВ), причем «пики» характерны для ядер с четным числом протонов

3

и нейтронов (42He, 126C, 168O), а минимумы – для ядер с нечетным числом протонов и нейтронов (63Li, 105B, 147 N).

Отметим для сравнения, что энергия связи валентных электронов в атомах составляет примерно 10 эВ (т.е. практически в 106 раз меньше).

Рис. 1.

Итак, уменьшение удельной энергии связи при переходе к тяжелым элементам объясняется тем, что с возрастанием числа протонов в ядре увеличивается и энергия их кулоновского отталкивания. Поэтому связь между нуклонами становится менее сильной, а сами ядра менее прочными.

Наиболее устойчивыми оказываются так называемые магические ядра, у которых число протонов или число нейтронов равно одному из магических чисел: 2, 8, 20, 28, 50, 82, 126. Особенно стабильны дважды магические ядра, у которых магическими являются и число протонов, и число нейтронов (этих ядер насчитывается всего пять: 42He, 168O, 4020Ca, 2048Ca, 20882Pb).

Из зависимости удельной энергии связи от массовых чисел (рис. 1) следует, что наиболее устойчивыми с энергетической точки зрения являются ядра средней части таблицы Менделеева. Тяжелые и легкие ядра менее устойчивы. Это означает, что энергетически выгодны следующие процессы:

1)деление тяжелых ядер на более легкие;

2)слияние легких ядер друг с другом в более тяжелые.

При обоих процессах выделяется огромное количество энергии; эти процессы в настоящее время осуществлены практически: реакции деления

и термоядерные реакции.

4

3. Ядерный парк. NZ-диаграмма стабильных и долгоживущих ядер

В природе существует и искусственно получено большое число нуклидов – ядер с различными Z и A. Всего известно около 3000 нуклидов, т.е. ядерный мир значительно богаче мира химических элементов (атомов). Среди необычных искусственно полученных изотопов, такие как 102He, 68C,

128O и 288O. Условно все известные ядра можно разбить на 2 группы:

1.Стабильные и долгоживущие (период полураспада T1/2 > 2 105

лет) с ненулевым процентным содержанием в естественной смеси (их 283).

2.Радиоактивные (более 2500).

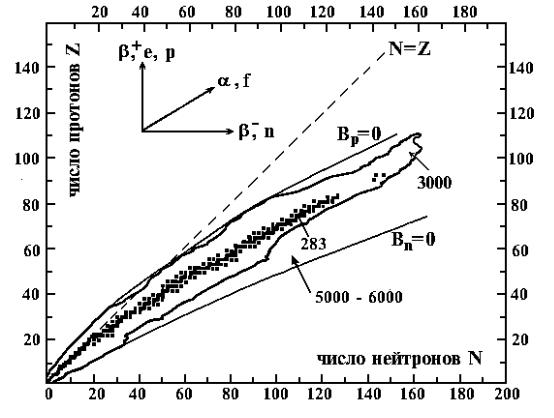
На рис. 2 приведена NZ-диаграмма стабильных и долгоживущих ядер. Легкие ядра следуют линии N = Z. Для тяжелых N > Z. Ниже будет показано, что за это отвечает кулоновское взаимодействие. Без него для всех стабильных ядер было бы N Z.

На диаграмме Bn и Bp – энергии отделения нейтрона и протона (минимальные энергии, необходимые чтобы удалить нуклон из ядра). Bn = Bp = 0 отвечает ситуация, когда добавляемый к ядру нуклон не захватывается ядром, т.е. вне линий Bn = 0 и Bp = 0 ядро долго не может существовать. Между линиями Bn = 0 и Bp = 0, где расположена область нуклидов с энергиями отделения нуклонов > 0, может быть 5000–6000 ядер. Эти числа определяют количество ядер, которое может быть получено искусственным путем.

Рис. 2. NZ-диаграмма стабильных и долгоживущих ядер

5

Ядро – система связанных нуклонов. Чтобы его разделить на составные нуклоны, нужно затратить минимальную энергию (2), называемую энергией связи ядра.

Энергия отделения нуклона BN (Bn или Bp) – это минимальная энергия, необходимая для вырывания нуклона из ядра. Очевидно, это энергия наиболее слабо связанного нуклона (сидящего выше всего в потенциальной яме).

Найдем энергию отделения Bn нейтрона. Отделению нейтрона отвечает процесс

(A, Z) (A–1, Z) + n.

Энергия, необходимая для такого процесса, определяется разностью масс (в энергетических единицах) после и до процесса, т.е.

Если отделяется сложная частица x(a, z), состоящая из нескольких нуклонов, то

где Есв(a, z) – энергия связи частицы x, уже не равная нулю.

Массы определяют либо из масс-спектроскопии, либо из баланса энергий в ядерных реакциях или распаде.

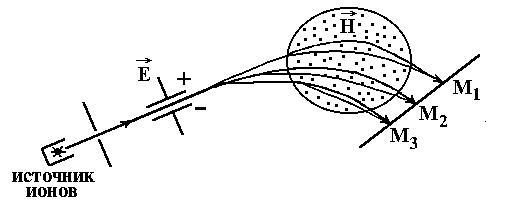
Принцип действия масс-спектрометра показан на рис. 3. Электрическое и магнитное поле выбираются так, чтобы ионы с различными скоростями, но одинаковыми Z/M, попадали в одно место фотопластинки или другого позиционно-чувствительного детектора. Относительная погрешность измерения массы 10–8–10–7.

Рис. 3. Схематическое изображение масс-спектрометра Международная атомная единица массы – 1/12 массы атома 12C

6

1 а.е.м. = масса атома 12C/12 =

= 931,49432(28) МэВ/c2 = 1,6605402(10) 10–27 кг.

Есв(A, Z) тем больше, чем больше A. Удобно иметь дело с так называемой удельной энергией связи (энергией связи на один нуклон)

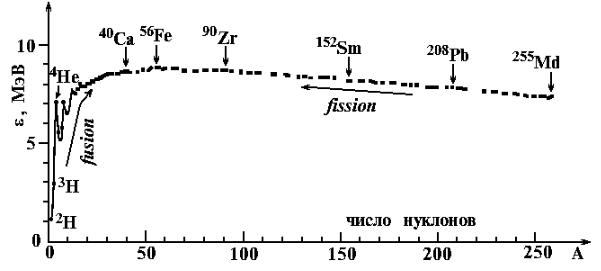
График этой величины для стабильных и наиболее долгоживущих тяжелых элементов дан на рис. 4. Для A > 20 удельная энергия 8 МэВ. Для разрыва химической связи (электромагнитные силы) нужна энергия в 106 раз меньше. С точки зрения запасов энергии 1 г ядерного топлива соответствует 10 тоннам химического топлива.

Рис. 4

Ядерную энергию можно получить двумя способами:

1.Синтез легких ядер (fusion).

2.Деление тяжелых ядер (fission).

В обоих процессах (показанных стрелками на рис. 4) совершается переход к ядрам, в которых нуклоны связаны сильнее, и часть энергии связи высвобождается.

Если разделить ядро с A 240 ( 7,6 МэВ) на два осколка равной массы A1 = A2 = 120 ( 8,5 МэВ), то освободится энергия 240 (8,5–7,6) МэВ = 220 МэВ.

Значение характеризует величину ядерного (сильного) взаимодействия. Гравитационная энергия двух нуклонов в ядре определяется величиной

где <rNN> = 2 фм – среднее расстояние между нуклонами, а G 1.3 10–42 фм с4/МэВ (c – скорость света) – гравитационная постоянная. Таким обра-

7

зом, гравитационная энергия двух нуклонов внутри ядра в 1037 раз меньше их ядерной энергии.

Кулоновская энергия двух протонов внутри ядра e2/<rNN> 0.7 МэВ, что примерно в 10 раз меньше ядерной.

Некоторые очевидные свойства ядерного взаимодействия:

1.Притяжение.

2.Короткодействие ( 1 фм).

3.Большая величина (интенсивность).

4.Насыщение (видно из рис (A)).

Поясним это последнее свойство. Для A > 20 const и Есв A, т.е. нуклоны взаимодействуют лишь с ближайшими соседями и удельная энергия связи быстро достигает предела ( 8 МэВ), т.е. насыщается. Если бы нуклоны внутри ядра взаимодействовали со всеми другими, то (при наличии двухтельных сил) Есв A(A–1) A2 (A >> 1), чего нет. Действительно, в этом случае энергия связи ядра была бы пропорциональна числу двухнуклонных связей, т.е. числу сочетаний из A по 2, которое как известно, равно

A(A–1)/2.

4. Спин ядра

Использование приборов высокой разрешающей способности и специальных источников возбуждения спектра позволило обнаружить сверхтонкую структуру спектральных линий. Ее существование В.Паули объяснил (1924) наличием у атомных ядер собственного момента импульса (спина) и магнитного момента.

Ядро, как пространственно ограниченная и связанная система взаимодействующих между собой нуклонов, во многих случаях может рассматриваться в целом как одна микрочастица. Так как нуклоны, из которых состоит ядро, обладают собственным механическим моментом, или спином, а также совершают движение относительно друг друга (орбитальное движение относительно центра инерции ядра), то и ядра должны иметь собственный механический момент или спин.

Собственный момент импульса ядра – спин ядра I –есть векторная сумма полных моментов Jk отдельных нуклонов, каждый из которых скла-

дывается из орбитального момента lk и спина нуклона sk , так что

k 1

Возможна другая схема сложения моментов отдельных нуклонов, когда сначала по отдельности суммируются векторы спинов и векторы орби-

8

тальных моментов всех нуклонов, затем полученные два вектора складываются. Однако, поскольку ядерные силы не центральны и в ядре существует спин-орбитальное взаимодействие, то по этой причине в теории ядра используют первую схему.

Естественной единицей измерения момента импульса в квантовой механике служит постоянная Планка ħ = 1,0546∙10–34 Дж∙с, имеющая размерность момента импульса.

Вектор момента любых микрочастиц, как, впрочем, и спина ядра, обладает своеобразными свойствами.

1. Абсолютная величина вектора момента любой изолированной физической величины может принимать только дискретные значения:

где I – спиновое ядерное квантовое число (его часто называют просто спином ядра), которое принимает целые или полуцелые положительные значения

Так как спиновое квантовое число нуклона s = 1/2, то ядра с четными А имеют целые I, с нечетными – полуцелые I.

Число I называют обычно величиной момента или квантовым числом момента. Следует особо отметить различие между модулем вектора I и квантовым числом I, так как последнее является одним из чисел (12), используемых в формуле (11) для нахождения модуля вектора I . Когда говорят: «момент 1/2», то имеют в виду именно это квантовое число в формуле (11).

В формуле (10) квантовое число lk для орбитального момента всегда целое число, lk = 0, 1, 2, … , а нуклоны (и электрон тоже) имеют квантовое число спина s = 1/2 (спин равен 1/2).

2. Мгновенное значение вектора любого механического момента не имеет смысла по той же причине, по которой в квантовой механике не имеет смысла мгновенное значение вектора импульса. Строго фиксированное значение может иметь только абсолютная величина вектора момента (11) и одна из его пространственных проекций, обычно называемой проекцией на

Реализация любой возможной проекции из набора (13) оказывается

равновероятной.

Число возможных проекций на ось Z четно, если I – полуцелое число, и нечетно, если I – целое число. Знак плюс или минус в (13) означает ориентацию вектора момента на выбранное направление оси Z в пространстве.

9

Однако величины проекций Ix и Iy не имеют определенных значений и флуктуируют относительно нулевого среднего значения. Учитывая, что

лютной величины вектора механического момента. Действительно, соглас-

Все перечисленные выше свойства вектора механического момента обычно демонстрируют с помощью квазиклассической модели (рис. 2), которая находится в определенном согласии со свойствами квантовомеханического вектора момента. Вектор момента, модуль которого вычисляется с помощью (11), прецессирует относительно оси Z с некоторой угловой скоростью и может ориентироваться вдоль или против направления оси Z только таким образом, чтобы его проекция на ось Z была равна одному из значений от +Iћ до –Iћ через единицу. Этот вектор никогда не может ориентироваться точно по направлению оси Z, поскольку его модуль, как отмечено выше, не равен Iћ. Поэтому, помимо его модуля, сохраняющейся во времени величиной является только одна проекция вектора – проекция на ось Z. Полное число проекций Iz вектора момента на рис.2 равно (2I+1).

3. Модуль вектора момента I3сложной системы, составленной из двух взаимодействующих систем с моментами I1 и I2, вычисляется из выражения

обычным образом через свои квантовые числа I3. Сложение векторов I1 и

I2 есть сложение их проекций как алгебраических чисел. Для получения возможных проекций вектора I3 каждая из проекций вектора I1 складыва-

ется с одной из соответствующих проекций вектора I2. Таких проекций оказывается всего (2I1+1)(2I2+1), которые будут образовывать (2Im+1) векторов I3, Im = min{I1, I2}, со следующими значениями квантовых чисел:

Соотношение (17) называется правилом сложения моментов в квантовой механике.

10