
FTF 4 semestr.DOBRO / Optika_otvety
.pdf
14. Основные понятия фотометрии
|
|
|
|
|
|
|
|
|
Раздел оптики, в |
котором рассматриваются методы измерения |
||
|
(1) |
|
|
|
|
(2) |
|
|||||
|
|
|
|
|
|
световой энергии, называется фотометрией. |
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
С точки зрения фотометрии, свет – это излучение, способное |
|||
|
|
|
|
|
|
|
|
вызывать ощущение яркости при воздействии на человеческий |
||||
(3) |
|
|
|
(4) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
глаз. Такое ощущение вызывает излучение с длинами волн от |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
~0,38 до ~0,78 мкм, причем самым ярким представляется излучение с |
|||
|
|
|
|
|
(6) |
|
|
|
||||
|
|
|
|
|
|
|
|
длиной волны |
около |
0,555 мкм |
(желто-зеленого цвета). Поскольку |
|
|
(5) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
чувствительность глаза к разным длинам волн у людей неодинакова, в |
|||
|
|
|
|
|
|
|
|
|
||||
|
(7) |
|
|
|
|
|
|
фотометрии принят ряд условностей. |
||||
|
|
|
|
|
|
|
|
|
Существуют два общих метода фотометрии: |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1) визуальная фотометрия, в которой при выравнивании |
|||
|
|
|
|
|
|
|
|
|
механическими или оптическими средствами яркости двух полей |
|||
|
|
|
|
|
|
|
|
|
сравнения используется способность человеческого глаза ощущать |
|||
|
|
|
|
|
|
|
различия в яркости; |
|
|
|||
|
|
|
|
|
|
|
|
|
2) физическая фотометрия, в которой для сравнения двух источников |
|||
|
|
|
|
|
|
|
|
|
света используются различные приемники света иного рода – |
|||
|
|
|
|
|
|
|
|
|
вакуумные фотоэлементы, полупроводниковые фотодиоды и т. д. |
|||
|
|
|
Величину |
энергии W, |
излучаемой |
телом |
за единицу |
времени t, называют мощностью |
||||
излучения: N=W/t.
Световым потоком Ф называют проходящую через данную поверхность S в единицу
времени t световую энергию, оцениваемую по зрительному ощущению  . Поток излучения Фе, имеющий физический смысл средней мощности, переносимой
. Поток излучения Фе, имеющий физический смысл средней мощности, переносимой
электромагнитным излучением. Пространственное распределение Фе описывают энергетические фотометрические величины, производные от потока излучения по площади и (или) телесному
углу. Полный поток, идущий от L по всем направлениям, будет  .
.
Поток есть основное понятие, необходимое для оценки количества энергии, проникающей в наши приборы. Знание потока существенно необходимо при расчете многих оптических устройств. Такой приемник, как, например, фотоэлемент, непосредственно реагирует на поток .
2. Сила света J. Величину потока, приходящегося на единицу телесного угла, называют силой света. Если поток Ф посылается нашим источником равномерно по всем направлениям, то I=Ф/4π (1.3) есть сила света, одинаковая для любого направления. В случае неравномерного потока величина Ф/4p представляет лишь среднюю силу света и называется средней сферической силой света. Сила света по данному направлению определится соотношением (1).
Освещенностью Е называется величина потока, приходящегося на единицу поверхности: Освещенность площадки s есть (3), (4). Выражение показывает, что освещенность, создаваемая точечным источником обратно пропорциональна квадрату расстояния от источника до поверхности и прямо пропорциональна косинусу угла, составляемого направлением светового потока (осью узкого конуса, внутри которого распространяется поток) с нормалью к освещаемой поверхности. Это есть основной закон освещенности, создаваемой точечным источником (закон обратных квадратов).

ИЛИ |
Коэффициент Вi носит название яркости источника по |
направлению, определяемому углом i. |
|
Светимость S.С понятием яркости тесно связано понятие светимости S, представляющей собой интегральную величину, т. е. суммарный поток, посылаемый единицей поверхности наружу по всем
направлениям (внутрь телесного угла 2p). Таким образом,
Для характеристики светового поля можно ввести еще понятие интенсивности светового потока. Под интенсивностью понимают величину светового потока, протекающего через единицу видимого сечения по направлению, определяемому углом i между направлением потока и нормалью к этому сечению, внутрь единичного телесного угла:
16.
Интерференция света, интенсивность при суперпозиции двух монохроматических волн.
Интерференцией называют явлении наложения 2-х или более когерентных колебаний
|
когерентных волн, приводящее к перераспределению |
||||
|
интенсивности света, те к появлению мах и мин. Когерентными |
||||
|
|
называются монохроматические колебания, имеющие |
|||
|
|
|
постоянную во времени и пространстве разность фаз. |
||
|
|
|
|
|
Пусть даны волны Е1 и Е2 имеют разные амплитуды и |
|
|
|
|
|
фазы, но одну частоту, тогда результ. амплитуда есть |
|
|
|
сумма этих амплитуд.Когда волны имеют одну частоту, разные |
||
|
амплитуды и соответствующие колебания в противофазе, то |
||||
результ. |
амплитуда есть разность амплитуд. Если же разности фаз |
||||
когерентных |
волн =0, то наблюдается мах при 2πn и min при (2n+1)π. Общее |
||||
правило |
сложения на рис. |
||||
|
Физическую величину, равную квадрату амплитуды электрического поля |
||||
|
|
|
|
|
волны, принято называть интенсивностью: I = A2. |
|
|
|
|
|
|
|
|
|
|
|
Несложные тригонометрические преобразования приводят |
|
|
|
|
|
к следующему выражению для интенсивности |
|
|
|
результирующего колебания в точке P (см рис) Из этого |
||
|
|
|
выражения следует, что интерференционный |
||
|
|
|
|
макс = mλ (m = 0, ±1, ±2, ...). При этом Imax = (a1 + a2)2 > I1 + I2. |
|
|
|
Интерференционный мин при = mλ + λ / 2. Минимальное |
|||
значение интенсивности Imin = (a1 – a2)2 < I1 + I2.
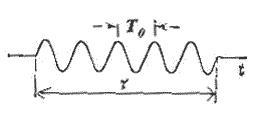
17. Временная и пространственная когерентность света. Измерение когерентности.
Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты. Необходимо отметить, что когерентность двух электромагнитных полей определяет независимость средней разности их полных фаз от времени. По этой причине отмечается роль времени в определении когерентности и её в соответствии с этим обстоятельством называют временной когерентностью.
Временной аспект когерентности имеет исключительно важное значение при рассмотрении явлений взаимодействия электромагнитных волн ввиду того, что, во-первых, в строгом смысле на практике монохроматических волн с абсолютно одинаковыми частотами не существует из-за статистического аспекта излучения электромагнитных волн. Во-вторых, монохроматические волны представляют собой в соответствии с определением бесконечный по продолжительности и локализации пространственно-временной процесс, что очевидно невозможно с точки зрения предположений о конечности энергии источников электромагнитных волн.
Таким образом, монохроматические волны в физике являются весьма полезной математической абстракцией, позволяющей досконально изучить основные свойства электромагнитных волн. На практике монохроматические волны представляются в виде цугов конечной длительности по времени (рис. 4.6), представляющих собой гармонические во времени функции, ограниченные во времени и пространстве о чём говорилось выше.
В связи с этим обстоятельством рассматривается время когерентности. Время когерентности учитывает тот факт, что реально средняя разность фаз может зависеть от времени. Поскольку когерентность двух волн связывается с возможностью наблюдения интерференционной картины, то под временем когерентности понимается время, в течение которого интерференционная картина этих волн может
наблюдаться. Конечно, возможность наблюдения интерференционной картины является субъективным фактором. Однако, выше мы рассмотрели понятие видности интерференционной картины (4.5). Видность интерференционной картины отлична от нуля при различии интенсивностей её максимумов и минимумов. Чем больше это различие, тем лучше видна интерференционная картина. Интерференционная картина не видна, когда интенсивность её максимумов совпадает с интенсивностью минимумов. При этом интерференционная картина как бы ' разрушается '. Упрощенно это можно представить с помощью наложения максимумов одной интерференционной картины на минимумы другой (рис. 4.7). Появление второй интерференционной картины следует из того факта, что наблюдается интерференция двух цугов волн, каждый из которых в зависимости от длительности цуга можно представить в виде суперпозиции того или иного количества плоских электромагнитных волн. По этой причине на экране наблюдается одновременно интерференция всевозможных пар монохроматических составляющих цугов волн. Для упрощения качественных рассуждений рассматривается только одна из возможных пар монохроматических составляющих для понимания эффекта разрушения интерференционной картины.
Возможность наблюдать интерференцию когерентных волн от протяжённых источников приводит к понятию пространственной когерентности электромагнитных волн. Для простоты рассуждений представим, что источники когерентных электромагнитных волн с одинаковыми начальными
фазами  и с длиной волны
и с длиной волны  расположены на отрезке длины d, расположенном на
расположены на отрезке длины d, расположенном на
расстоянии  от экрана (рис. 4.9), на котором наблюдается их интерференция. Наблюдаемая на экране интерференционная картина может быть представлена как наложение интерференционных картин, создаваемых бесконечным множеством пар точечных когерентных источников, на которые можно мысленно разбить протяжённый источник.
от экрана (рис. 4.9), на котором наблюдается их интерференция. Наблюдаемая на экране интерференционная картина может быть представлена как наложение интерференционных картин, создаваемых бесконечным множеством пар точечных когерентных источников, на которые можно мысленно разбить протяжённый источник.

Например, в точках минимума интерференционной картины волн от близко расположенных источников интерференционная картина пространственно разделенных источников будет иметь максимальное значение. Вследствие этого значения максимумов и минимумов интерференционной картины протяжённого источника при увеличении его длины будут иметь близкие значения и видность интерференционной картины будет стремиться к нулю. В рассматриваемом случае это
имеет место при |
в (4.20). Значение длины отрезка |
, соответствующее этому |
условию определяется из соотношения:  .
.
В оптике и теории электромагнитных волн половина этого значения определяет т.н. радиус пространственной когерентности  электромагнитных волн, излучаемых протяжённым
электромагнитных волн, излучаемых протяжённым
источником:  Физический смысл понятия радиуса пространственной когерентности протяжённого источника состоит в представлении о возможности наблюдения интерференционной картины от
Физический смысл понятия радиуса пространственной когерентности протяжённого источника состоит в представлении о возможности наблюдения интерференционной картины от
протяжённого источника, если он размещается внутри круга, диаметр которого равен  . Из сказанного следует вывод, что пространственная когерентность электромагнитных волн определяется угловым размером их источника. С угловым размером источника можно связать направления прихода волн от него. От удалённых источников, в точку наблюдения приходят волны, которые с большой степенью точности можно считать плоскими. По этой причине от каждой из точек протяжённого источника в точку наблюдения приходит плоская волна, направление которой слегка отличается от направления волны, излучаемой соседней точкой источника. Совокупность плоских волн, приходящих от источника излучения в точку наблюдения называется пространственным спектром излучения этого источника. Объёмом когерентности
. Из сказанного следует вывод, что пространственная когерентность электромагнитных волн определяется угловым размером их источника. С угловым размером источника можно связать направления прихода волн от него. От удалённых источников, в точку наблюдения приходят волны, которые с большой степенью точности можно считать плоскими. По этой причине от каждой из точек протяжённого источника в точку наблюдения приходит плоская волна, направление которой слегка отличается от направления волны, излучаемой соседней точкой источника. Совокупность плоских волн, приходящих от источника излучения в точку наблюдения называется пространственным спектром излучения этого источника. Объёмом когерентности
называется  и равен произведению длины когерентности
и равен произведению длины когерентности 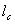 на площадь круга радиуса
на площадь круга радиуса  :
:
 .
.
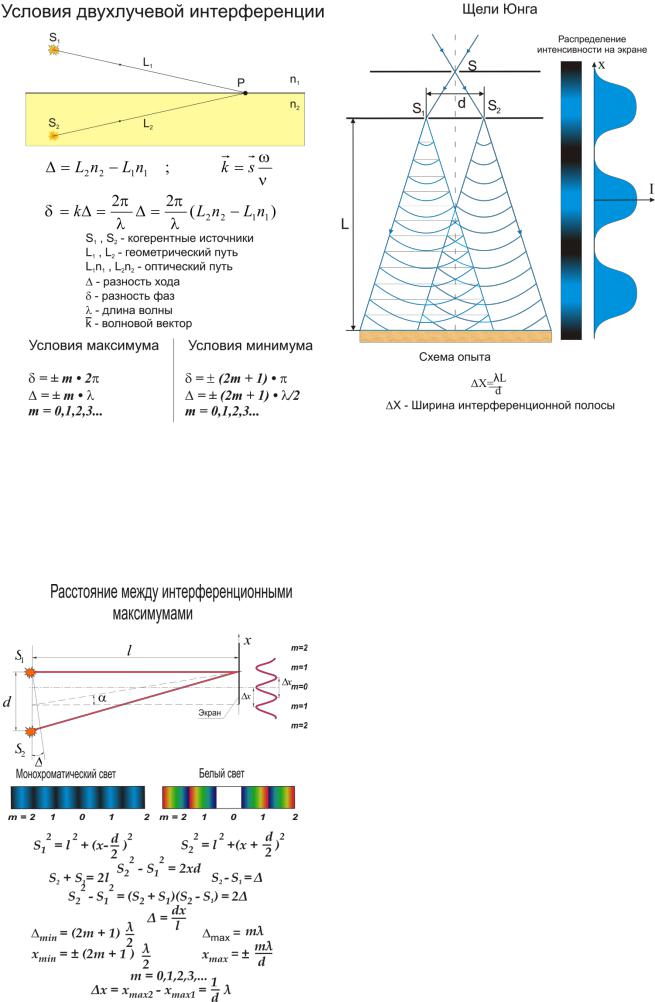
18. Двухлучевая интерференция. Опыт Юнга. Ширина интерференционной полосы.
Для рассмотрения лучевой интерференции, рассмотр. источники S1 и S2,
находящ. в разных средах. S1 нах-ся в среде с показ прелом. n1, S2 – c n2; l1геометрич путь в среде n1; l2-геометрич путь в среде n2. Произведение ln назся оптический путь, – разность хода. Если Δ=+-mλ, то наблюдается мах интенсивности; Если Δ=+-(2m+1), то есть укладывается нечетное число длин волн, от мин освещ.

19. Классические интерференционные схемы. Бипризма Френеля. Зеркала Френеля.
Бизеркала Френеля. Два плоских соприкасающихся зеркала располагаются так, что их отражающие поверхности образуют угол, близкий к 180°. Источник света (например, узкая светящаяся щель) помещается
параллельно линии пересечения зеркал на расстоянии OS = r |
от неё. |
||||
ВспомогательныйэкранККпреграждаетсветупутьотисточникаSкэкрануАА. |
|||||
Источниками когерентных |
волн S1 |
и S2 |
служат |
два |
мнимых |
изображения источника света S. |
Мнимые |
источники S1 |
и S2 |
взаимно |
|
когерентны, исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрытия. (Можно показать, что максимальный угол расхождения перекрывающихся пучков не может быть больше2α).НаоснованиизаконовотраженияSи S1 расположеныотносительно
зеркала I симметрично, длина отрезка OS1 |
равна OS, т. е. r . Аналогично |
|
относительно зеркала II |
OS2 OS r . |
Поэтому расстояние между |
источниками S1 и S2 равно d |
=2r sinα ≈2r α. |
|
Расстояниеотмнимыхисточниковдолиниипересечениязеркал
a r cosα ≈ r
Расстояние S1S
междузеркаламиα.
.Следовательно, L= a + b , где b –расстояниеотлиниипересечениязеркалOдоэкранаАА.
2 = d тем меньше и, следовательно, интерференционная картина тем крупнее, чем меньше угол
Бипризма Френеля состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами (порядка нескольких минут). Параллельно этому
основанию на расстоянии a от него располагается источник света S. Свет от источника преломляется в обеих призмах, в результате чего за бипризмой распространяются световые
пучки, как бы исходящие из мнимых источниковS1 и S2 |
, |
являющихся когерентными. На экране происходит наложение когерентныхсветовыхпучковинаблюдаетсяинтерференция.
Так как преломляющий угол бипризмы очень мал и малыуглыпадениясветовыхлучейнабипризму,можносчитать,чтоуглыотклонениялучей ,падающихнаверхнююи
нижнююполовинкибипризмымалы,амнимыеизображенияисточникасветаисамисточникрасположеныпрактически воднойплоскости: n 1 .Расстояниемеждуисточникамиравно d 2a sin 2a 2a n 1 .
Расстояние от источников до экрана: L a b . Для наблюдения широких полос интерференции необходимо
обеспечить малое расстояние d = |
S1S2 |
, при этом поле интерференции оказывается малым. |
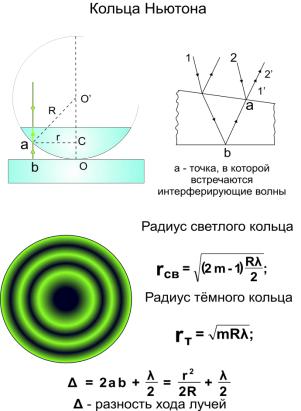
20. Интерференция в тонких пленках. Полосы равной толщины. Полосы равного наклона. Кольца Ньютона.
 При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от верхней и нижней поверхности плёнок (рис. 4.16). Для белого света, представляющего собой смешение электромагнитных волн из всего оптического спектра интерференционные полосы приобретают окраску. Это явление получило название цветов тонких плёнок. Цвета тонких плёнок наблюдаются на стенках мыльных пузырьков, на плёнках масла, нефти, на поверхности металлов при их закалке (цвета побежалости).
При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от верхней и нижней поверхности плёнок (рис. 4.16). Для белого света, представляющего собой смешение электромагнитных волн из всего оптического спектра интерференционные полосы приобретают окраску. Это явление получило название цветов тонких плёнок. Цвета тонких плёнок наблюдаются на стенках мыльных пузырьков, на плёнках масла, нефти, на поверхности металлов при их закалке (цвета побежалости).
Для объяснения этих явлений рассмотрим расположенную в вакууме плоско параллельную
диэлектрическую пластинку (рис.) толщины  с показателем преломления
с показателем преломления  , где
, где  - диэлектрическая проницаемость диэлектрика освещаемую плоской световой монохроматической
- диэлектрическая проницаемость диэлектрика освещаемую плоской световой монохроматической
волной с длиной волны  под углом
под углом  (рис. 4.16). При отражении световых волн от верхней и нижней поверхности пластинки между отражёнными волнами возникнет оптическая разность хода , которая является следствием того факта, что волна, отражённая от нижней поверхности пластинки проходит больший путь внутри диэлектрической пластинки, чем волна, отраженная от верхней границы.
(рис. 4.16). При отражении световых волн от верхней и нижней поверхности пластинки между отражёнными волнами возникнет оптическая разность хода , которая является следствием того факта, что волна, отражённая от нижней поверхности пластинки проходит больший путь внутри диэлектрической пластинки, чем волна, отраженная от верхней границы.
Система для получения колец Ньютона состоит из плосопаралельной стекл. пластины, на которой расположении линза с большим радиусом кривизны. Воздушный зазор между линзой и пластиной играет роль клина на котором наблюдается интерф. картина.
21. Интерферометры: Майкельсона, Линника, Рождественского.
Интерферометр — измерительный прибор, принцип действия которого основан на явлении интерференции. Принцип действия интерферометра заключается в следующем:
пучок электромагнитного излучения (света, радиоволн и т. п.) с помощью того или иного устройства пространственно разделяется на два или большее количество когерентных пучков. Каждый из пучков проходит различные оптические пути и возвращается на экран, создавая интерференционную картину, по которой можно установить смещение фаз пучков. Интерферометры применяются как при точных измерениях длин, в частности в станкостроении и машиностроении, так и для оценки качества оптических поверхностей и проверки оптических систем в целом.
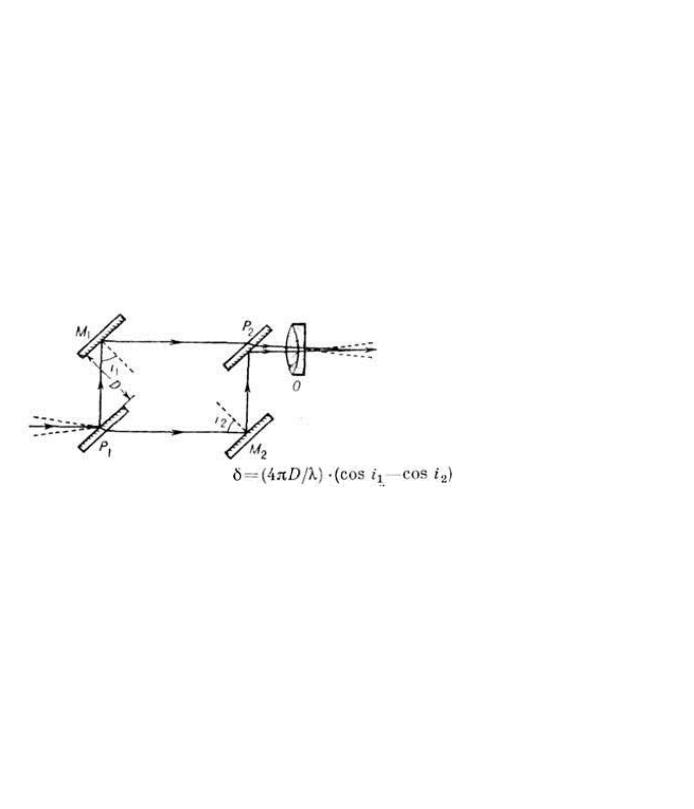
ИНТЕРФЕРОМЕТР РОЖДЕСТВЕНСКОГО- двухлучевой интерферометр, состоящий из двух зеркал М1, М2 и двух параллельных полупрозрачных пластин P1 P2 (рис. 1); M1,
|
P1 и M2, Р2 устанавливаются попарно |
|
параллельно, но М1 и М2 наклонены |
|
относительно друг друга на малый угол; |
|
расстояние М 1 Р 1=М 2 Р 2 и М 1Р 2=Р 1M2. |
|
Луч света разделяется пластиной Р 1 на 2 |
|
луча, к-рые после отражений от М1, М2 и |
|
прохождения Р2 оказываются |
параллельными с разностью фаз |
. Поскольку d не зависит от |
положения лучей на зеркалах и определяется лишь углами падения, интерференц. картина будет локализована на бесконечности (или в фокальной плоскости объектива О). Параллельному пучку лучей, падающих на И. Р., соответствует одна точка интерференц. картины, и, следовательно, для наблюдения всей картины необходим пучок конечной апертуры. Вид картины (порядок и ширина полос, их ориентация) зависит от наклона зеркал М1 и М2. Если, напр., ребро двугранного угла, образованного М1 и M2, вертикально (перпендикулярно чертежу), то даже при очень малой разности (i1-i2) полосы сравнительно высокого порядка (D велико) вертикальны и почти параллельны. Если же ребро двугранного угла горизонтально, то в поле зрения находятся горизонтальные полосы низкого порядка (в т. ч. нулевая), видные и в белом свете. Введение в один из пучков к.-л. прозрачного объекта, напр, пластинки, изменяет ширину, порядок и ориентацию полос: нулевая полоса не горизонтальна и появляется при нек-рой промежуточной
ориентации М1 и M2; при очень большой толщине этой пластинки в белом свете можно видеть только очень узкие, почти вертикальные полосы, когда ребро угла между М1 и М2 почти вертикально. Схема, аналогичная рис. 1, применяется в т. н. интерферометре Маха - Цендера; отличие его от И. Р. состоит в том, что попарно параллельно устанавливаются М1, М2и Р1, Р2. При этом можно получить полосы равной толщины, если точно совместить изображения S' и S
" источника света S, образованные в двух ветвях интерферометра (рис. 2). Полосы локализованы в плоскости этого изображения, равно как и в плоскости S "', сопряжённой с S' через объектив O2, где и ведётся наблюдение. Если в пучок лучей вблизи S' и S " поместить оптически неоднородную среду (напр., поток воздуха), то полосы изменят свою форму, наглядно показывая распределение показателя преломления в исследуемой среде. Ширина полос зависит от угла
между М1 и P1t увеличиваясь с его уменьшением. Если все зеркала и пластины параллельны, то в отсутствие неоднородностей ширина полос бесконечна (интерференц. поле равномерно
освещено). Введение неоднородностей приводит к появлению полос, форма к-рых соответствует кривым разных значений показателя преломления.
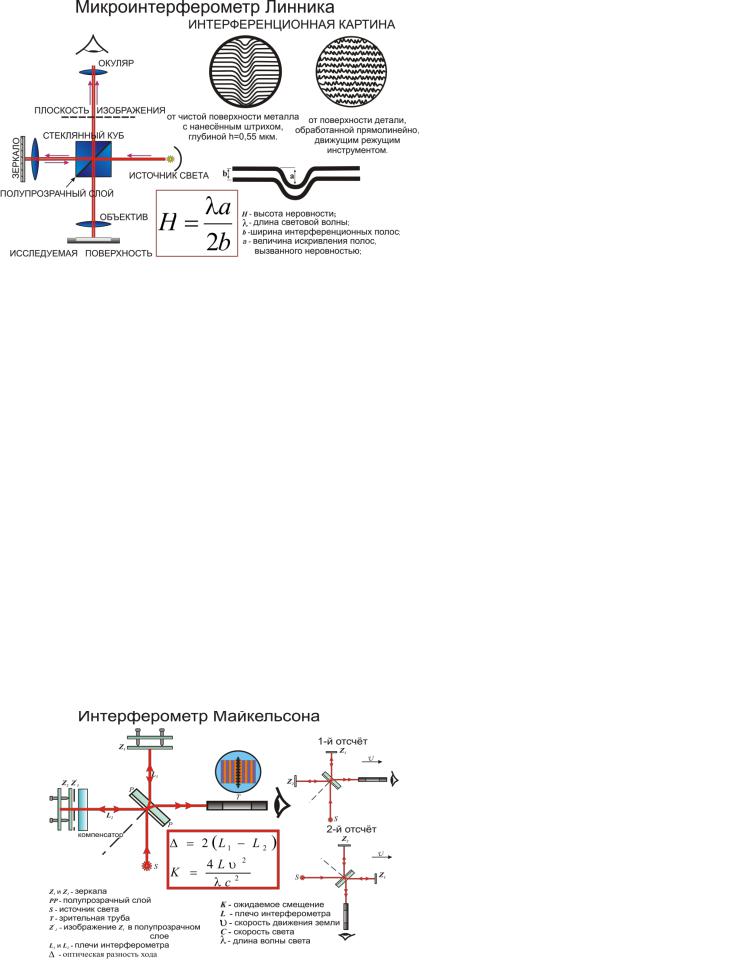
Интерферометр Линника
Собственно, интерферометр Линника представляет собой слегка видоизмененный интерферометр Майкельсона и может быть назван и так и этак. Мы здесь обсудим не столько его устройство, сколько его
применение для определения качества обработки поверхностей.
Основу интерферометра составляют две стеклянные пластины p1 и p2 и два зеркала, одним из
которых служит исследуемая поверхность.
Нижняя поверхность первой пластины представляет собой полупрозрачное зеркало, на котором происходит разделение лучей: часть света (луч 1) отражается вверх, отражается от исследуемой поверхности и после отражения от нижнего зеркала З" направляется в окуляр (на рисунке не показан), через который и наблюдается интерференционная картина.
После прохождения пластины p1 луч 2 направляется к зеркалу З, отражается от него, затем от полупрозрачного зеркала и вместе с лучем 1 направляется к наблюдателю.
Луч 1 после отражения от полупрозрачного зеркала и на обратном пути дважды проходит через пластину p1, "набирая" тем самым некоторую "лишнюю" разность хода. Для ее компенсации служит пластина p2, изготовленная из того же материала, что и первая. Разумеется, эту "лишнюю разность хода" можно было бы легко скомпенсировать простым перемещением зеркала, если бы не было дисперсии, зависимости коэффициента преломления от длины волны n(l). Применение компенсирующей пластины p1 позволяет осуществить такую компенсацию сразу для всех длин волн. Почему образуется интерференционная картина и как она выглядит помогает понять укрупненный фрагмент рисунка слева вверху. Реальный луч 2 и его отражение от зеркала З можно заменить лучем 2' и его "отражением" от изображения зеркала З в полупрозрачном зеркале - З'. Это изображение и исследуемая поверхность образуют клин, пластину изменяющейся толщины. Соответственно, через окуляр наблюдаются интерференционные линии равной толщины - прямые, направленные перпендикулярно плоскости рисунка. И эти линии видны искривленными, если исследуемая поверхность не вполне плоская. При "идеально" плоской поверхности это прямые линии.
Интерферометр Майкельсона —
двухлучевой интерферометр, изобретённый Альбертом Майкельсоном. Данный прибор позволил
впервые измерить длину волны света. В опыте Майкельсона интерферометр был использован Майкельсоном для
проверки гипотезы о светоносном эфире. Конструктивно состоит из светоделительного
зеркала, разделяющего входящий луч на два, которые в свою очередь, отражаются зеркалом обратно. На полупрозрачном
зеркале разделённые лучи вновь направляются в одну сторону, чтобы смешавшись на экране, образовать интерференционную картину. Анализируя её и изменяя длину одного плеча на известную величину, можно по изменению вида интерференционных полос измерить длину волны, либо, наоборот, если длина волны известна, можно определить неизвестное изменение длин плеч. Радиус когерентности изучаемого источника света или другого излучения определяет максимальную разность между плечами интерферометра.
Устройство используется[1] и сегодня в астрономических, физических исследованиях, а также в измерительной технике. В частности, интерферометр Майкельсона лежит в основе оптической схемы современных лазерных гравитационных антенн.
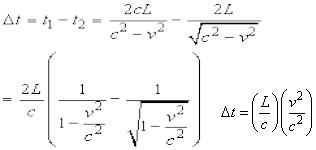
Если интерферометр покоится относительно эфира, то время, затрачиваемое первым и вторым лучами света на свой путь, одинаково, и в детектор попадают два когерентных луча в одинаковой фазе. Следовательно, возникает интерференция, и можно наблюдать центральное светлое пятно на интерференционной картине. Если же интерферометр движется относительно эфира, то время, затрачиваемое лучами на свой путь, оказывается разным. Действительно, пусть c – скорость света относительно эфира, а v – скорость интерферометра относительно эфира. Тогда время,
затрачиваемое на первый путь (по течению и обратно) равно  .
.
Для вычисления времени t2 следует учесть, что пока свет путешествует от полупроницаемой перегородки до зеркала М2, само зеркало движется вместе с Землей относительно эфира. Поэтому путь, пройденный светом до зеркала М2, равен гипотенузе треугольника. Скорость света при этом не меняется, так как свет движется перпендикулярно направлению скорости Земли. Из простых
геометрических соображений  . Итак, разность времен.
. Итак, разность времен.
Пользуясь приближенными формулами:
 можно получить, что
можно получить, что
.Такой задержке во времени соответствует разность путей двух лучей света
 Следовательно, такой разности хода лучей будет соответствовать полное число
Следовательно, такой разности хода лучей будет соответствовать полное число
длин волн света, уложившихся на этой разности хода, равное  .
.
Интерференционные максимумы и минимумы чередуются при изменении разности хода на λ/2. Таким образом, вычислив значение n для конкретных параметров установки и зная скорость Земли, можно узнать, как должны сдвинуться интерференционные полосы. Конечно, эффект весьма мал. Для его усиления Майкельсон максимально увеличил базу интерферометра L, заставив свет многократно отражаться от дополнительных зеркал. Кроме того, опыт был проделан вторично при повернутом на 90 градусов приборе, за счет чего лучи меняются местами и эффект сдвига интерференционных полос удваивается.
