Методические указания к выполнению контрольной работы

Если некоторые условия ограничивают движение тела в одном или нескольких направлениях, то такое тело называется несвободным.

Тела, которые ограничивают движения рассматриваемого тела, называются связями. Действие связи на тело называют реакциями связи. Направление реакции связи противоположно тому направлению, по которому связь препятствует движению тела. Сила, с которой тело действует на связь, называется силой давления на связь. Сила реакции и сила давления на связь равны по модулю, но противоположны по направлению.

Последовательность решения задач на равновесие несвободных тел:

1. Выяснить, какое тело (точка) в данной задаче находится в состоянии равновесия, и приложить к нему заданные силы.

2. Выделенное тело освободить от связей и их действия заменить реакциями.

3. Выбрать координатные оси и составить уравнение равновесия.

4. Решить уравнение равновесия.

5. Проверить правильность решения задачи.

Методику решения задач с помощью уравнения равновесия рассмотрим на примерах.

Для решения первой задачи (№ 1-10), которая относится к теме 1.2 «Плоская система произвольно расположенных сил», требуется составить уравнения проекций на координатные оси и уравнения моментов.

Проекция вектора – скалярная величина, которая определяется отрезками, отсекаемыми перпендикулярными, опущенными из начала и конца вектора на ось.

Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону.

Моментом силы относительно точки называется произведение модуля силы на плече, т.е. на длину перпендикуляра, восстановленного из точки, относительно которой берется момент, к линии действия силы. Момент принято считать положительным, если он стремится повернуть тело по часовой стрелке, и отрицательным, если вращение направлено в противоположную сторону.

Пример 1. Для балки (рис. 1) определить опорные реакции по следующим данным: a=1.5 м, b=1 м, c=2 м, F₁=8 кН, F₂=10 кН, q=0.4 кН/м, М=5 кН*м.

Решение. Освободим балку от связей, отбросив опоры и приложив вместо них неизвестные реакции (рис. 1). Напомним, что для плоской системы параллельных сил достаточно двух уравнений равновесия

Рис. 1

Уравнения моментов относительно точки А:

Уравнения моментов относительно точки B:

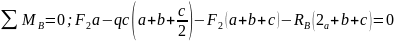
Из первого уравнения

Из второго уравнения

Значение реакции R_B получено со знаком минус. Это означает, что она направлена вертикально вниз.

Для проверки правильности найденных реакций опор балки составляем уравнение

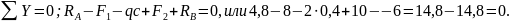
Следовательно, R_A и R_B определены, верно.

Вторую задачу контрольной работы (11-20) следует решать после изучения тем «Основные понятия кинематики» и «Кинематика точки». В задачах рассматривается равнопеременное движение точки. Следует учесть, что при использовании уравнения равнопеременного движения точки по криволинейной траектории кроме касательного ускорения, у точки возникает нормальное ускорение , направленное по радиусу кривизны траектории к ее центру.

Для решения задач используются соответствующие готовые уравнения и формулы, выведенные в учебниках. Решение задач целесообразно иллюстрировать рисунками.

РР

Рис. 2

Пример 2. По дуге радиусом r = 1200 м (рис. 2) движется поезд, его скорость в начале движения по дуге составляет V₀ = 60 км/ч.

После того как поезд прошел расстояние 800 м, его скорость уменьшилась до 36 км/ч. Определить полное ускорение в начале и конце движения.

Решение. Определим касательное ускорение из уравнений:

Из второго уравнения

Из первого уравнения

Так как движение равномерно замедленное, то касательное ускорение в течение всего времени движения постоянно.

Найдем нормальное ускорение:

В начале движения

В конце движения

Полное ускорение:

В начале движения

В конце движения

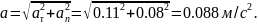
Третью задачу контрольной работы (21-30) следует решать после изучения тем «Простейшие движения твердого тела», «Основные понятия и аксиомы динамики», «Метод кинетостатики для материальной точки». Рассматривая вращательное движение твердого тела, необходимо отчетливо уяснить, что вращение тела характеризуется угловыми величинами (угол поворота φ, угловая скорость ω и угловое ускорение ε), а отдельные точки вращающегося тела совершают криволинейное движение (по окружностям) и их движение характеризуется линейными величинами (пусть s, скорость v и ускорение a_τ, a_n). При решении задач динамики необходимо пользоваться принципом Даламбера, в каждый данный момент действующее на материальную точку силы уравновешиваются силами инерции.

Пример 3. Маховик диаметром 0,8 м начинает вращаться из состояния покоя. Через 10 с после начала движения скорость точек обода маховика достигает 8 м/с. Определить ускорение этих точек. Чему равно число оборотов маховика за первые 10 с равнопеременного вращения?

Решение. По значению скорости точки находим угловую скорость вращения маховика через 10 с после начала вращения:

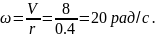
Угол поворота маховика за 10 с

Число оборотов маховика за 10 с

Угловое ускорение маховика

Нормальное ускорение точек обода маховика в момент t = 10 с

Касательное ускорение точек обода маховика

Пример 4. Груз массой 200 кг (рис. 3) опускается равноускоренно с помощью невесомого троса, перекинутого через блок, и в первые 5 с. проходит 10 м. Определить силу натяжения троса.

Решение. Обозначив груз точкой А, приложим к нему силу тяжести G, реакцию троса Т и добавим к нему силу инерции F_и, направив ее в сторону, противоположную ускорению.

Ускорение, а определяем из уравнения равнопеременного движения , так как начальная скорость :

Согласно принципу Даламбера силы G, T и F_и находятся в равновесии, т.е. 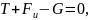откуда T= G- F_и. Выражая силу инерции и силу тяжести через массу груза ( ), получаем

Рис. 3

К решению четвертой задачи контрольной работы (№ 31-40) следует приступать после изучения темы «Растяжение и сжатие», метода сечений и разбора решенных примеров в данном пособии и рекомендуемой литературе.

Задача требует умения определить продольные силы, нормальные напряжения, удлинения и построения эпюр N и σ.

Растяжением (сжатием) называют такое нагружение бруса, при котором в поперечных сечениях возникает только один внутренний силовой фактор – продольная сила N, в любом поперечном сечении бруса численно равная алгебраической сумме внешних сил, действующих на оставленную часть бруса.

Правило знаков: внешняя сила N, направленная от сечения, считается положительной; в противном случае она отрицательна.

Удлинение (укорочение) бруса, или отдельных его участков, определяется по формуле Гука

∆l = Nl/AE,

которую можно представить еще и в виде ∆l = σ (l/E), помня, что N/A = σ.

Пример 5. Для двухступенчатого бруса (рис.5) определить и построить эпюры продольных сил и нормальных напряжений. Определить удлинение (укорочение) бруса. Модуль упругости E = 2*10⁵ МПа.

Решение. Разделим брус на участки, границы которых определяются сечениями, границы которых определяются сечениями, где изменяется площадь поперечного сечения или приложены внешние нагрузки. Мысленно рассечем Рис. 5

брус в пределах первого участка и отбросим верхнюю часть бруса (рис.5, б). Сила F₁ уравновешивается внутренней силой.

N₁ = F₁ = 40*10³ Н = 40 кН.

Аналогично в пределах участка II (рис.5, в) отбросим верхнюю часть бруса и рассмотрим оставленную часть бруса с действующей силой F₁, которая уравновешивается продольной силой N_II:

N_II = F₁ = 40*10³ Н = 40 кН

Продольная сила на участке III (рис.5, г) уравновешивается в сечении внешними силами F₁ и F₂ и равна их алгебраической сумме

N_III = F₁ – F₂ = 40*10³ – 50*10³ = - 10*10³ Н = - 10кН.

Построим эпюру N (рис.5, д). Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее ее откладываем значение продольной оси, вызванной сжатием участка, а правее – растяжением. В пределах участка III брус сжат (N_III = -10 кН), в пределах участков II и I брус растянут (N_II = N_I = 40 кН).

Для определения напряжений в поперечных сечениях значение продольных сил разделить на площади соответствующих сечений.

Площадь поперечного сечения бруса в пределах участка I

аналогично на участках II и III

Находим напряжения на отдельных участках бруса и строим эпюру (рис.5, е):

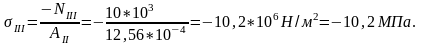
В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений.

Полное удлинение бруса равно алгебраической сумме удлинений его участков:

или

К решению пятой задачи (№41-50) следует приступить после изучения темы «Кручение» и разбора решенного примера.

В соответствии с Международной системой единиц (СИ) заданную в условии частоту вращения n, мин^-1, необходимо выразить в единицах угловой скорости (рад/с), применив формулу Тогда зависимость между передаваемой мощностью P, кВт, угловой скоростью ω, рад/с, и внешним моментом M, Н*м, скручивающим вал, запишется в виде M=P/ω.

Допускаемый угол закручивания на практике обычно задается в град/м, поэтому для перевода в единицы СИ это значение необходимо умножить на π/180⁰. Например, если дано [φ⁰]=0,4 град/м, то 0,4 град/м=0,4π/180⁰=0,07 рад/м.

Пример 6. Для стального вала определить из условия прочности требуемые диаметры каждого участка и углы закручивания этих участков. Угловую скорость вала принять ω=100 рад/с, P₁=30 кВm, P₂=0,5P₁, P₃=0,3 P₁, P₄=0,2P₁ допускаемое напряжение [τ]=30 МПа, модуль упругости сдвига G=0,8*10¹¹Па=8*10⁴МПа.

Рис. 6

Решение. Вал вращается с постоянной угловой скоростью, следовательно, система вращающих моментов уравновешена. Определяем мощности на шкивах P₂=0,5P₁=0,5*30=15кВm; P₃=0,3 P₁=0,3*30=9кВm; P₄=0,2P₁=0,2*30=6кВm.

Определяем вращающие моменты на шкивах:

M₁ = P₁/ω = 30*10³/100 = 300 Н*м;

M₂ = P₂/ω = 15*10³/100 = 150 Н*м;

M₃ = P₃/ω = 9*10³/100 = 90 Н*м;

M₄ = P₄/ω = 6*10³/100 = 60 Н*м.

Для построения эпюр крутящих моментов проведем базовую (нулевую) линию параллельно оси вала и, используя метод сечений, найдем значения крутящего момента на каждом участке, отложим найденные значения перпендикулярно базовой линии.

В пределах каждого участка значение крутящего момента сохраняется постоянным:

М_К1=-М₄=-60Нм

М_К2=-М₄-М₃=-60-90=-150Нм

М_К3=М₂=-М₄-М₃+М₁=-60-90+300=150Нм

Из условия прочности диаметр вала на первом участке определяется по формуле

,

откуда

На втором участке

На третьем участке

Определяем полный угол закручивания, исходя из того, что вал поделен на 3 участка

φ= φ₁+ φ₂+ φ₃

Определяем углы закручивания по формуле

, град

Определяем полярный момент инерции для каждого участка

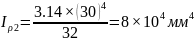
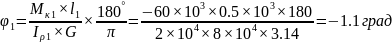
Определяем полный угол закручивания

φ=  1.1 0.8+0.94= 0.96град

Шестую задачу контрольной работы (51-60) следует решать после изучения темы «Изгиб» и внимательного разбора примеров 14 и 15 настоящего пособия.

При прямом поперечном изгибе в поперечных сечениях балки возникает два внутренних силовых фактора – поперечная сила Q и изгибающий момент M_и. Поперечная сила, возникающая в произвольном поперечном сечении, численно равна алгебраической сумме всех внешних сил (если все силы параллельны оси y), действующих на балку по одну сторону от рассматриваемого сечения.

Изгибающий момент в произвольном поперечном сечении численно равен алгебраической сумме моментов всех внешних сил, действующих на балку по одну сторону от рассматриваемого сечения относительно той точки продольной оси балки, через которую проходит рассматриваемое сечение.

Для отыскания опасного сечения строят эпюры Q и M_и, используя метод сечения.

Условимся о правиле знаков: внешняя сила F, стремящаяся сдвинуть левую часть балки вверх относительно правой или (что то же самое) правую часть вниз относительно левой, вызовет возникновение положительной поперечной силы (рис.7, а).

Внешняя сила или момент, изгибающие балку таким образом, что сжатые волокна находятся сверху балки (рис. 7, б), вызывают положительный изгибающий момент, который на эпюре M_и откладывается вверх от оси абсцисс, т.е. в сторону сжатых волокон, иначе можно сказать, что эпюры изгибающих моментов строятся на сжатом волокне.

Для балок, имеющих много участков нагружения, т.е. нагруженных комбинацией нагрузок, целесообразно строить эпюры по характерным сечениям, а именно: вычислить поперечные силы и изгибающие моменты только для сечений, в которых эпюры претерпевают изменения, а затем, зная закон изменения эпюры между найденными сечениями, соединить их соответствующими линиями. К характерным относятся сечения, в которых приложены сосредоточенные силы или моменты, а также сечения, где начинается или кончается распределенная нагрузка.

Рис. 7

Для того чтобы вычислить поперечную силу и изгибающий момент в произвольном сечении, необходимо мысленно рассечь плоскость в этом месте балку и часть балки (любую), лежащую по одну сторону от рассматриваемого сечения, отбросить. Затем по действующим на оставленную часть балки внешним силам надо найти искомые значения Q и M_и, причем знак их надо определить по тому действию, какое оказывают внешние силы на оставленную часть балки в соответствии с принятым ранее правилом знаков.

При построении эпюры слева направо отбрасывается правая часть балки, а Q и M_и находятся по силам, действующим на левую часть. При построении эпюры справа налево, наоборот, отбрасывается левая часть, а Q и M_и определяется по силам, действующим на правую часть балки.

Для построения эпюр необходимо запомнить следующие правила.

1. На участке балки, где отсутствует распределенная нагрузка, эпюра Q – прямая, параллельная базовой линии, а эпюра M_и – наклонная прямая.

2. Под сосредоточенной силой на эпюре Q наблюдается скачок, численно равный приложенной внешней силе, а на эпюре M_и – излом.

3. В точке приложения сосредоточенной парой сил на эпюре момента происходит скачок на размер момента этой пары, а эпюра Q не претерпевает изменения.

4. На участке действия равномерно распределенной нагрузки эпюра Q выражается наклонной прямой, а эпюра M_и – параболой, обращенной выпуклостью навстречу действию распределенной нагрузки.

5. Если на участке действия распределенной нагрузки эпюра пересекает базовую линию, то в этом сечении изгибающий момент принимает значение.

6. Если на границе действия распределенной нагрузки не приложено сосредоточенных сил, то на эпюре Q участок, параллельный оси абсцисс, переходит в наклонный без скачка, а параболическая и наклонная части эпюры M_и сопрягаются плавно без изгиба.

7. Изгибающий момент в концевых сечениях балки всегда равен нулю, за исключением случая, когда в концевом сечении действует сосредоточенная пара сил. В этом случае изгибающий момент в концевом сечении балки равен моменту действующей пары сил.

8. В сечении, соответствующем заделке, Q и M_и численно равны опорной реакции и реактивному моменту.

Решать задачу рекомендуется в такой последовательности:

1.определить реакции опор балки (по двум уравнениям моментов – дно относительно левой опоры, второе относительно правой), а

затем обязательно проверить правильность решения по уравнению проекций на ось, перпендикулярную балке;

2.построить эпюру поперечных сил;

3.построить эпюру изгибающих моментов;

4.по эпюре изгибающих моментов определить расчетный ( наибольший по абсолютному значению) изгибающий момент, выразив его ньютоно-метрах (Н*м);

5.в выражении условия прочности σ = M_и/W_x ≤ [σ] принять σ = [σ] и определить осевой момент сопротивления поперечного сечения балки;

6.выразить значение W_x в мм³ (при подстановке в расчетную формулу W_x = M_и/[σ] значения M_и выражаются в Н*мм, а значения [σ] – в МПа, результат получим в мм³)

Пример 7. Для балки (рис.8) построить эпюры поперечных сил и изгибающих моментов, если сила F=8 кН, интенсивность равномерно распределенной нагрузки q=4кН/м, момент M=11кН*м, расстояние a=2м, b=4м, c=3м. Определить размеры поперечного сечения. Принять =10 МПа

Решение. Определим опорные реакции:

;

,

откуда

;

,

откуда

.

Для проверки составляем сумму проекций всех сил на вертикальную ось y:

,

.

Строим эпюру поперечных сил (рис.8).

В сечении K: Q_K = 0.

В сечении A: Q_Aлев = - qa = -4*2 = -8 кН;

Q_Aправ = - qa+R_A = -8+11=3 кН.

В сечении А: на эпюре Q получается скачок на величину реакции R_A.

В сечении D:

Q_Dлев = qa+R_A = - 4*2+11 = 3 кН;

Q_Dрав = -qa+R_A-F = -8+11-8 = -5 кН.

В сечении B:

Q_B = - R_B = -5 кН.

Строим эпюру изгибающих моментов по характерным сечениям K, A, D, B (рис.8).

В сечении K изгибающий момент М_иK=0, так как в этом сечении нет сосредоточенного момента.

В сечении A рассмотрим левую часть, на которую действует равномерно распределенная нагрузка:

.

В сечении B действует сосредоточенный момент M:

М_иB = - M = -11 кН*м.

В сечении D рассмотрим правую часть, на которую действует сила R_B и сосредоточенный момент M:

M_иD = R_Bc – M = 5*3-11 = -4 кН*м.

Соединим полученные точки эпюры на участках DB и AD наклонными прямыми, на участке AK – параболой, обращенной выпуклостью навстречу равномерно распределенной нагрузке.

Определим размеры поперечных сечений

Для круга

Для прямоугольника h=2b

=94 мм

Задача 12. Прямолинейное движение точки определяется уравнением где s – в метрах, t – в секундах. Определить скорость v, пройденный путь s и ускорение, а через 10 с после начала движения.

Задача 13. Уравнение прямолинейного движения точки где s – в метрах, t – в секундах. Определить время t, в течении которого скорость тела достигает 10 м/с, пройденный за это время путь s и ускорение а.

Задача 14. Тело падает с высоты Н=78,4 м. определить время падения t и скорость v в момент достижения Земли.

Задача 15. При отходе от станции поезд через 3 мин набрал скорость v=64,8 км/ч. Определить ускорение и пройденный путь s за указанное время.

Задача 16. Поезд, проходя мимо разъезда, затормозил и далее двигался равнозамедленно. Через 4 мин он остановился на станции, находящейся на расстоянии 2 км от разъезда. Определить скорость v₀ в начале торможения и ускорение а.

Задача 17. Свая после удара копрового молота углубляется в землю равнозамедленно в течение 0,02 с. с начальной скоростью v₀=5м/c. Определить необходимое число ударов молота, чтобы заглубить сваю на 1500 мм.

Задача 18. Тело брошено вертикально вверх с начальной скоростью 490 м/с. Определить высоту и время подъема.

Задача 19. Поезд, отходя от станции, движется равноускоренно по закругленному пути радиусом r = 600 м. определить касательное а_τ, нормальное а_n и полное ускорение поезда через 3 мин, когда пройденный путь равен 1620 м.

Задача 20. Точка движется из состояния покоя и за время t =15 с ее скорость увеличивается до v = 20 м/с. Определить пройденный точкой путь и ее полное ускорение в конце 15 с, считая движение равноускоренным по дуге окружности радиуса r = 500 м.

Задача 21. Какую силу надо приложить к телу массой m = 90,0 кг, лежащему на гладкой горизонтальной поверхности, чтобы оно приобрело скорость v = 8 м/с через 4 с?

Задача 22. Груз массой m = 450 кг подвешенный на стальном канате, спускается вниз с ускорением а_τ = 2,5 м/с² . Найти натяжение стального каната.

Задача 23. Груз массой m = 20 кг поднимается на веревке равноускоренно. Определит ускорение а_τ, при котором натяжение веревки будет равно 300 Н.

Задача 24. Шкив диаметром 500 мм передает мощность P = 8 кВт при частоте вращения n = 710 мин^-1 . Определить вращающий момент и окружную силу.

Задача 25. При передаче мощности P = 7,5 кВт на ободе колеса диаметром d = 80 мм действует окружная сила F = 500 Н. Определить угловую скорость колеса, считая его вращение равномерным.

Задача 26. Автомобиль массой 1500 кг под действием силы тяги F = 1150 Н движется равноускоренно по горизонтальному пути с начальной скоростью v = 18 км/ч. Определить время t, необходимое для достижения скорости v = 72 км/ч, и ускорение a автомобиля.

Задача 27. Сколько времени должна действовать сила F = 500 Н, приложенная к покоящемуся телу массой m = 130 кг, если она сообщит телу скорость v = 25 м/с? Какой путь пройдет тело под действием силы, если оно перемещается по гладкой горизонтальной плоскости?

Задача 28. Какую силу нужно приложить к автомобилю массой m = 1500 кг, движущемуся по прямолинейному горизонтальному пути со скоростью v = 70 км/ч, для того чтобы за время t = 15 с его скорость уменьшилась до 20 км/ч? Какой путь пройдет при этом автомобиль?

Задача 29. Определить, какую силу надо приложить к телу массой m = 300 кг, движущемуся прямолинейно, чтобы на пути s = 200 м его скорость уменьшилась с 20 до 10 м/с. Найти время движения тела до полной остановки, пренебрегая силой трения, если значение действующей силы не изменится.

Задача 30. Самолет массой 3500 кг для взлета должен иметь скорость 180 км/ч. На разгон самолета тратится время t = 30 с. Определить среднее значение силы тяги самолета (силой сопротивления движению самолета пренебречь).