Дискретные и непрерывные случайные величины. Ряд распределения. Интегральная и дифференциальная функции распределения.

Студент должен знать:

- понятие случайной величины и ее виды;

- способы задания случайной величины;

- закон распределения случайной величины;

Студент должен уметь:

- строить ряд распределения случайной величины;

- находить функцию распределения случайной величины.

Литература: [5] стр.60-72 .

Основные теоретические сведения

Величина, которая в результате опыта может принимать те или иные значения называются случайной величиной. Например, время ожидания автобуса на остановке, число свободных мест в вагоне поезда и т. д. Обозначать случайные величины будем заглавными латинскими буквами X, Y, Z и т. д.

Случайная величина называется дискретной, если мы можем перечислить все ее возможные значения и указать вероятность каждого значения.

Возможных значений может быть бесконечно много. Обычная дискретная величина задается рядом распределения в виде следующей таблицы.

X				. . .
P				. . .

Здесь, - все возможные различные значения случайной величины, а - вероятности, с которой случайная величина принимает соответствующие значения,

Не всегда можно задать случайную величину, указав вероятность каждого отдельного значения. В ряде случаев вероятность каждого отдельного значения равна 0. Любую случайную величину можно задать, указав ее функцию распределения.

Функция F(x)=P(X<x) называется интегральной функцией распределения случайной величины X или просто функцией распределения.

Функция распределения обладает следующими свойствами.

1. Монотонностью, то есть, если то

2. Для любых справедливо

3. 

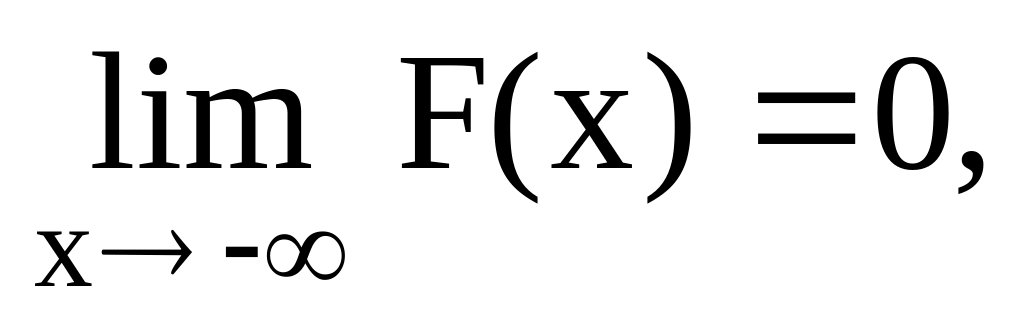
С помощью функции распределения можно подсчитать вероятность попадания случайной величины Х в интервал [a, b).

Назовем случайную величину непрерывной, если непрерывна ее функция распределения F(x).

Заметим, что в этом случае вероятность каждого значения случайной величины равна нулю.

Будем считать, что существует функция такая, что

при всех .

В этом случае функцию назовем плотностью распределения случайной величины Х или дифференциальной функцией распределения. Справедливо равенство

Вероятность попадания случайной величины Х в интервал (а,b) можно посчитать по формуле .

Свойство плотности распределения .

Примеры

Пример 1. Имеется 10 деталей, из них 6 стандартные. Составить ряд распределения числа стандартных деталей из двух выбранных.

Решение: Очевидно, что при выборе двух деталей, число стандартных деталей может оказаться равным 0, 1, 2, то есть мы имеем дело с дискретной случайной величиной. Найдем вероятность, с которой принимается каждое значение, и составим ряд распределения. Считаем, что выбор каждой детали равновозможен, и применим для нахождения вероятностей классическое определение.

Число всех возможных исходов для выбора двух исправных деталей равно .

Число благоприятных вариантов для выбора только нестандартных деталей равно .

Число благоприятных вариантов для выбора одной исправной детали равно .

Число благоприятных вариантов для выбора только стандартных деталей равно .

Таким образом,

Составим ряд распределения.

Х	0	1	2
Р

Для проверки убедимся, что сумма вероятностей равна 1.

Пример 2. В партии из семи деталей четыре окрашенные. Наудачу взяты три детали. Построить ряд и многоугольник распределения случайной величины - числа окрашенных деталей среди отобранных.

Решение: Случайная величина может принять следующие четыре значения: , , , . Вероятности этих значений равны:

, ,

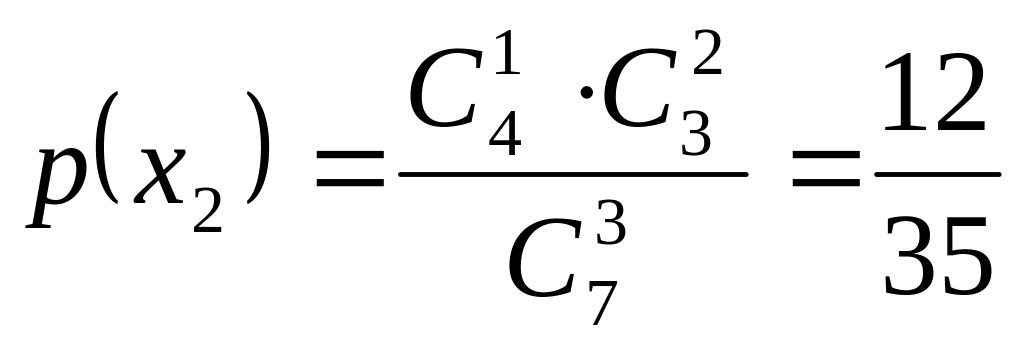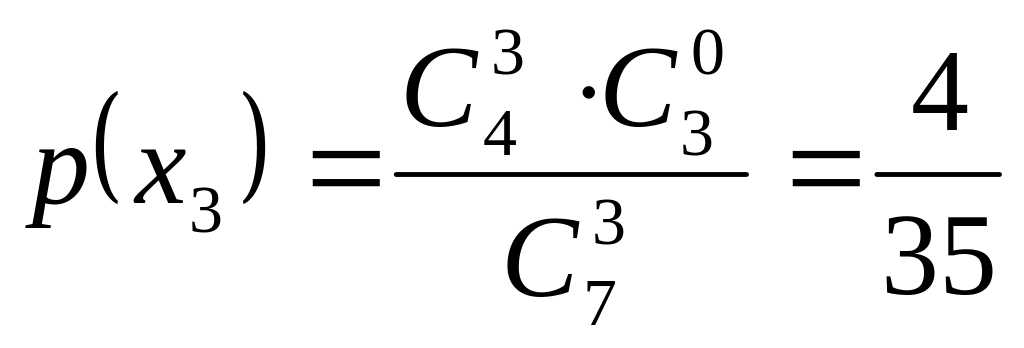
Складывая полученные вероятности, имеем:

.

Составим ряд распределения:

x	0	1	2	3
p	1/35	12/35	18/35	4/35

Построим многоугольник распределения случайной величины Х (рис.4).

Рисунок 4. Многоугольник распределения

Пример 3. Найти интегральную функцию распределения случайной величины Х, заданной рядом распределения. Построить ее график.

	-1	0	2
p	0,1	0,4	0,5

Решение. Чтобы найти вероятность события Х< x, разобьем числовую ось на интервалы точками – 1, 0 и 2. Если , то событие невозможно и в этом случае . Если то событие имеет место тогда и только тогда, когда , то есть

1 0 2 х

Если , то событие может произойти только в том случае, если Х = 1 или Х = 0, то есть

И, наконец, если , то событие достоверно и

На координатной плоскости построим график (рис.4).

F(x)

1

0,5

0,1

1 0 2 x

Рисунок 5. График интегральной функции распределения

Пример 4. Дискретная случайная величина Х задана законом распределения

X	1	4	8
p	0,3	0,1	0,6

Найти функцию распределения и начертить ее график.

Решение: Если , то , поскольку случайная величина не принимает значений меньших 1.

Если , то .

Если , то – на этом интервале принимает значение 1 с вероятностью 0,3 и значение 4 с вероятностью 0,1. Поскольку эти события несовместны, то по теореме сложения вероятностей 0,3+0,1=0,4.

Если , то .

Итак, функция распределения аналитически может быть записана так:

График данной функции:

Рисунок 5. График функции распределения.

Пример 5. Найти функцию плотности непрерывной случайной величины, заданной функцией распределения

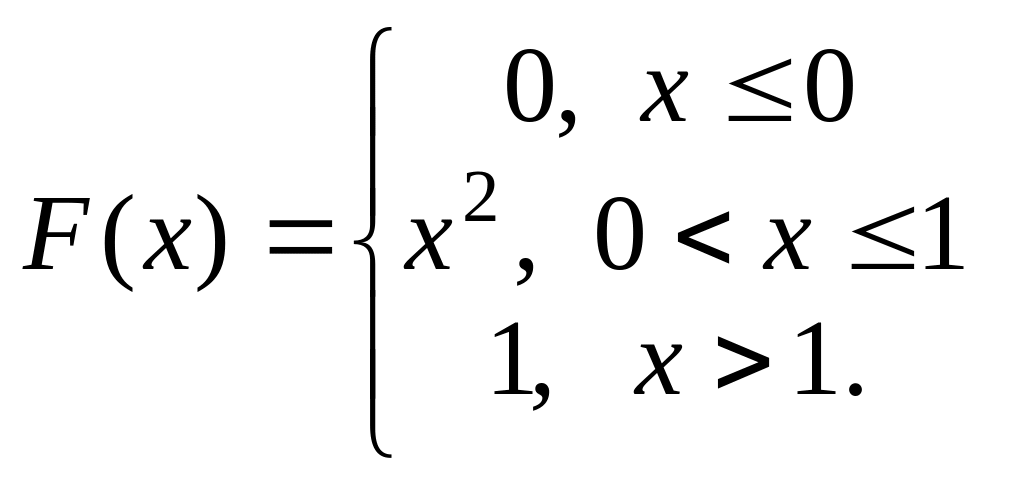
Построить графики функций F(x) и f(x). Найти вероятность попадания в интервал .

Решение. Найдем дифференциальную функцию распределения (функцию плотности):

Построим график функции распределения (рис. 6) и график дифференциальной функции распределения (рис. 7)

F(x)

1

0 1 x