10.4. Ламинарное напорное течение в зазоре

(Определение скорости, расхода и потерь при ламинарном течении в зазоре, образованном двумя параллельными плоскими стенками)

Для гидродинамической теории смазки важным является рассмотрение течения в зазоре между двумя плоскими параллельными пластинками под действием сил давления и сил трения. Этот случай позволяет в дальнейшем использовать полученные зависимости для течения в концентрическом зазоре.

Рис.10.5. Ламинарное течение в зазоре

Расстояние между двумя параллельными стенками равно а (рис. 10.5). Начало координат взято в середине зазора, ось Ох вдоль течения, а ось Оу - по нормали к стенкам.

При равномерном и установившемся движении жидкости рассматривается равновесие объема в виде прямоугольного параллелепипеда, расположенного симметрично относительно оси Ох.

Размеры параллелепипеда l –длина, b – ширина, 2у- высота. Силы, действующие на выделенный объем, где 2у*b – площадь, 2l*b – площадь поверхности сверху и снизу

(10.13)

где р_тр = р₁- р₂ – разность давлений в рассматриваемых сечениях. Знак минус, потому что производная ∂V/∂y отрицательна, 2l*b, так как напряжение действует на двух поверхностях – сверху и снизу.

Приращение скорости ∂V, соответствующее приращению координаты

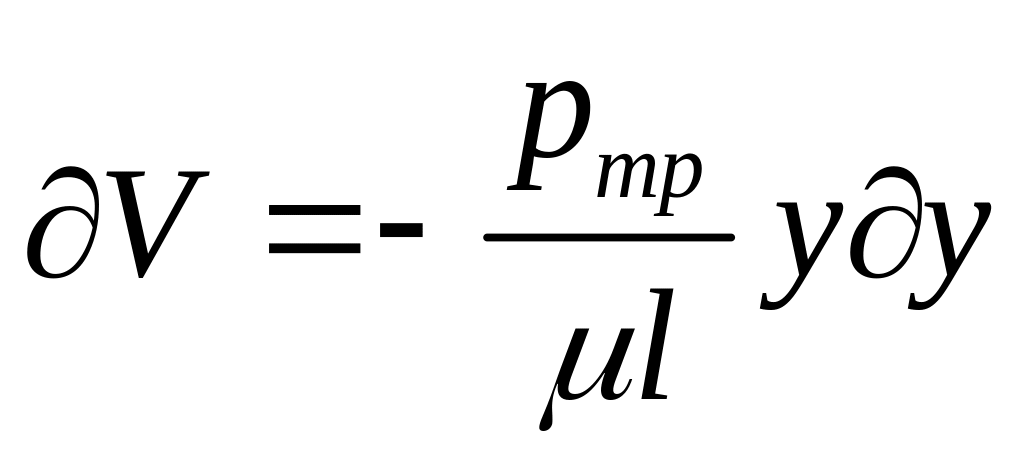
После интегрирования получим: . При начальных условиях на стенке y = a/2, V = 0 находим

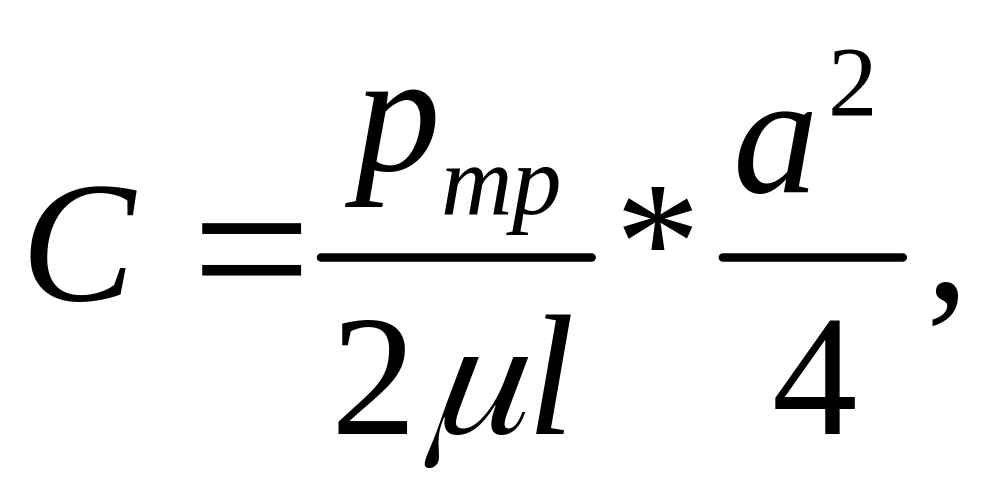
Скорость при ламинарном течении в плоском зазоре

, (10.14) .

При у=0 максимальная скорость

Для определения расхода q, приходящегося на единицу ширины потока при b=1, возьмем симметрично относительно оси z две элементарные площадки S= 2b*δy = 2δy, выразим элементарный расход

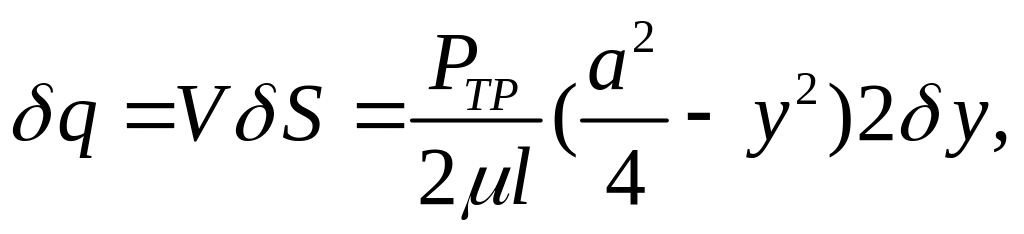
перейдя к дифференциалам и интегрируя, получим расход при b=1

Выразим потерю давления на трение через полный расход Q= q*b при зазоре шириной b ≠ 1;

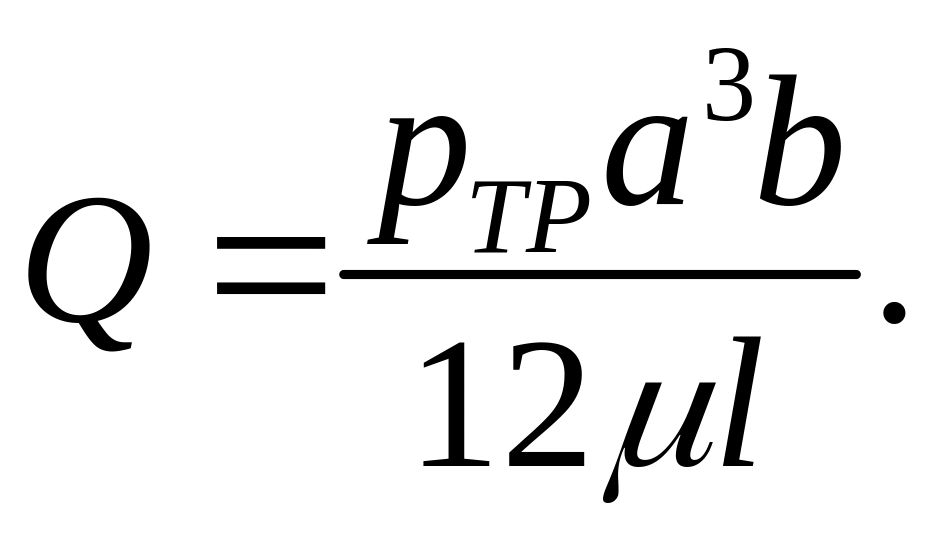
Используя выражение для полного расхода, получим потери давления при течении в плоском зазоре

(10.15)

10.5. Ламинарное безнапорное течение в зазоре.

Фрикционное безнапорное движение жидкости, когда одна из стенок, образующих зазор, перемещается параллельно другой, например, при движении пластинки положенной на жидкость и неподвижном дне сосуда, при отсутствии давления в зазоре. Подвижная стенка увлекает за собой жидкость.

Рассматриваем равновесие в потоке элемента dx*dy*b, как показано на рис.10.6.

Давления, приложенные к левой и правой граням элемента одинаковы (напора – нет). Hа элемент действуют силы трения, вызываемые касательными напряжениями на нижней грани – τ и на верхней грани τ+δ τ. Из-за неодинаковой скорости по сечению элемент жидкости притормаживается снизу

Рис.10.6.Фрикционное безнапорное движение

После еще одного интегрирования

Постоянные С и С₁ найдем при y = 0, V = u₀/2 и при y = a/2, V = u₀. Отсюда

где u₀– скорость стенки, а – ширина зазора.

После подстановки С и С₁ в последнее уравнение получим закон распределения скоростей при безнапорном течении

Расход жидкости q определяется по средней скорости y=0, .

Если перемещение стенки происходит при перепаде давления в жидкости, заполняющей зазор, то закон распределения скоростей найдем, как сумму или разность для напорного и фрикционного движения жидкости.

Скорость напорного движения

Скорость фрикционного движения

При совпадении силы давления жидкости и направления движения стенки сумма скоростей

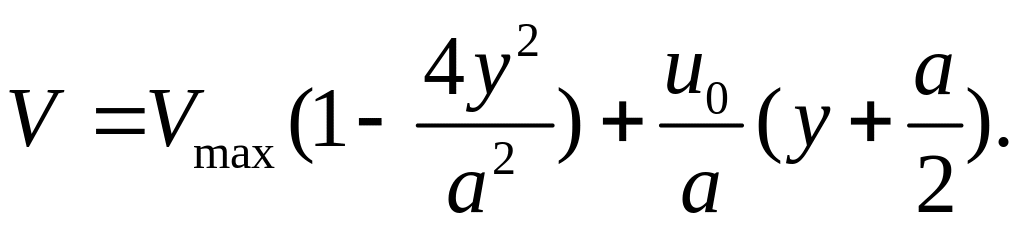
При несовпадении

Рис.10.8. Напорное и фрикционное движение с одной движущейся стенкой. а) движется верхняя стенка, б) движется нижняя стенка

При несовпадении силы давления жидкости и направления движения стенки

Распределение скоростей в зазоре показано на рис.10.8 в двух вариантах:

а) направление движения стенки совпадает с направление течения жидкости под действием перепада давлений;

б) направление движения стенки противоположно течению жидкости.

Расход жидкости через зазор единичной ширины в этих случаях определится как сумма расходов, выражаемых предыдущими формулами, для b=1

где - скорость напорного, u₀- бенапорного движения.

Первое слагаемое формулы называется расходом напорного течения, а второе — фрикционным расходом.