Необходимый и достаточный признак коллинеарности двух векторов.
Теорема: Для
того, чтобы вектор
был коллинеарен ненулевому вектору
,
необходимо и достаточно, чтобы существовало
число к
, удовлетворяющее условию
.
Разложение вектора на плоскости по двум неколлинеарным векторам
Теорема: Любой
вектор
может быть представлен и, притом,
единственным образом, в
виде линейной комбинации двух любых
неколлинеарных векторов
и
.
Дано: и неколлинеарны;
произвольный вектор плоскости.
Доказать:
1.
существует;
2. единственным образом.
Доказательство:
1. Докажем, что разложение существует.
П
усть
и
коллинеарны,
следовательно, по признаку коллинеарности
двух векторов
.
Значит,
верно равенство
.
Пусть и коллинеарны, следовательно, по признаку коллинеарности двух векторов . Значит, верно равенство .
О
Пусть
неколлинеарен векторам
и
(
;
).
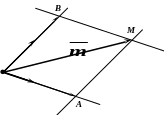
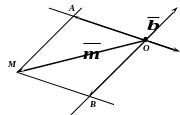
Через конец вектора проведем прямые, параллельные векторам и . Прямые, которым принадлежат векторы и , продолжим до пересечения с построенными прямыми, достраивая параллелограмм ОАМВ.
;
и
коллинеарны,
следовательно, по признаку коллинеарности
двух векторов
.
и
коллинеарны,
следовательно, по признаку коллинеарности
двух векторов
.
;
,
что
и требовалось доказать.
2. Единственность разложения доказывается методом от противного.
Замечание:
Если
,
то говорят, что вектор
разложен
по векторам
и
.
Базис плоскости. Декартова система координат на плоскости.
Прямоугольная декартова система координат на плоскости
Определение: Базисом плоскости называется пара неколлинеарных векторов этой плоскости, взятых в определенном порядке.
– базис плоскости,
где
.
Определение: Декартовой системой координат на плоскости называется множество, состоящее из точки О и базиса плоскости.
– декартова система
координат на плоскости .
О – начало координат;
О х – ось абсцисс;
О у – ось ординат.
Замечание: Любой
вектор
может
быть единственным
образом разложен по базисным векторам
и
:
.
Числа х и
у называются
координатами вектора
в данной
декартовой системе координат.
О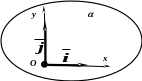
пределение:
Декартова
система координат на плоскости называется
прямоугольной, если базисные векторы
взаимно перпендикулярны и единичны.
– прямоугольная
декартова система координат на плоскости.
.
О – начало координат;
Ох – ось абсцисс;
Оу – ось ординат.
Замечание:
1. Базисные векторы
в прямоугольной
декартовой системе координат называются
ортами.
2. Любой
вектор
может
быть единственным
образом разложен по ортам
:
.
Числа х и
у являются
координатами вектора
в данной
прямоугольной декартовой системе
координат.
Упражнения:
1.
Доказать, что
и
коллинеарны.
2
.
В прямоугольнике АВСD проведены
диагонали АС и ВD , пересекающиеся в
точке О.
,
.
Выразить через
и
следующие векторы:
Декартова система координат в пространстве
4. 1. Понятие компланарных векторов
Определение: Ненулевые вектора называются компланарными, если они параллельны одной и той же плоскости.
Замечание: Любые два вектора всегда компланарны, а три вектора могут и не быть компланарными.
Векторы
компланарны, а
векторы
компланарными не являются.
4. 2. Разложение вектора в пространстве по трем некомпланарным векторам
Теорема:
Если даны три некомпланарных вектора
,
то любой вектор
можно разложить по векторам
единственным
образом.
Дано: некомпланарные векторы;
произвольный вектор пространства.
Доказать: 1.
существует;
2. единственное.
4.3. Базис пространства. Декартова система координат в пространстве. Прямоугольная декартова система координат в пространстве
Определение: Базисом пространства называются три некомпланарных вектора, взятых в определенном порядке.
базис пространства.
О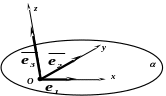
пределение:
Декартовой системой координат в
пространстве называется множество,
состоящее из точки О и базиса пространства.
- декартова
система координат в пространстве.
О – начало координат;
Ох – ось абсцисс;
Оу – ось ординат;
Оz – ось аппликат.
Замечание: Любой
вектор
может
быть единственным
образом разложен по базисным векторам
:
.
Числа х,
у, z
называются координатами вектора
в данной
декартовой системе координат.
О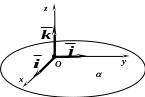
пределение:
Декартова
система координат в пространстве
называется прямоугольной, если базисные
векторы попарно взаимно перпендикулярны
и единичны.
– прямоугольная
декартова система координат в пространстве.
.
О – начало координат;
Ох – ось абсцисс;
Оу – ось ординат;
Оz – ось аппликат.
Замечание:
1. Базисные
векторы
в прямоугольной
декартовой системе координат называются
ортами.
2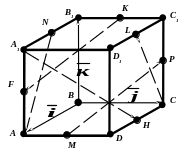
.
Любой вектор
может
быть единственным
образом разложен по ортам
:
.
Числа х,
у,
z
являются координатами вектора
в данной
прямоугольной декартовой системе
координат.
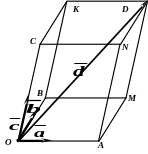
Пример:
Дано: ABCDA1B1C1D1 – куб.
;
;
.
M – середина AD;
H – середина DC;
F – середина AA1;
N – середина A1 B1;
K – середина B1 C1;
L – середина D1 C1;
P – середина C1 C.
Разложить
векторы
по векторам
.
Решение:
Воспользуемся «правилом многоугольника» сложения нескольких векторов:
;
;
;
;
.
Упражнения:
Дан куб ABCDA1B1C1D1. Являются ли компланарными следующие векторы:
а)
г)
б)
д)
в)
е)
2. В кубе ABCDA1B1C1D1
за базис взяты векторы
;
;
;
M – середина A1 B1; N – середина B1 C1; S – середина BC; Q – середина AD;
R
– середина CD ; T
– середина BB1; P
– середина AB. Разложить
по базису
векторы
.
Построение точек плоскости (пространства), заданных координатами
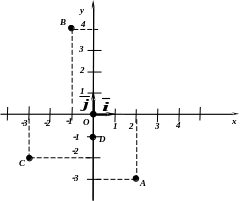
Пример:
Построить в
точки
А(2; 3);
В ( 1; 4);
С ( 3; 2);
D(0; 1).
П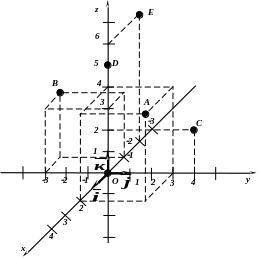
ример:
Построить в
точки
А(2; 3; 4);
В ( 1; 3; 3);
С (0; 4; 2);
D(0; 0; 5);
Е( 2; 0; 6).
Понятие радиус-вектора точки. Разложение радиус-вектора точки по ортам
Определение; Радиус-вектором точки называется вектор, начало которого совпадает с началом координат, а конец с данной точкой.
Вывод:
1. Каждой точке плоскости (пространства) соответствует свой радиус-вектор.
2. Координаты радиус-вектора точки совпадают с координатами самой точки.
3. Сумма произведений координат радиус-вектора точки М на соответствующие орты называется разложением радиус-вектора точки М по ортам.
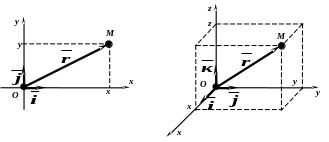
Рис. 1. Рис. 2.
Рис. 1.
В
точка М
(х; у) имеет
радиус-вектор
.
Рис. 2.
В
точка М (х; у; z)
имеет радиус-вектор
.
Упражнения:
Определить координаты орт в
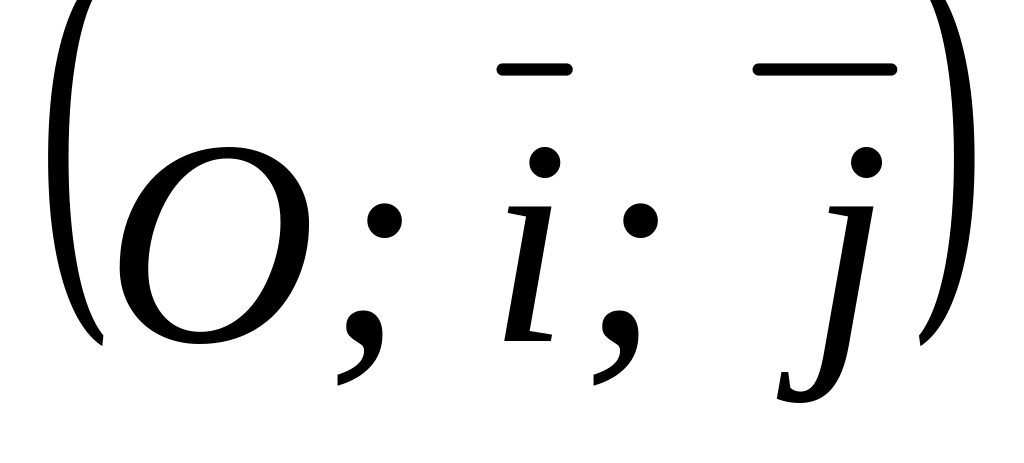и
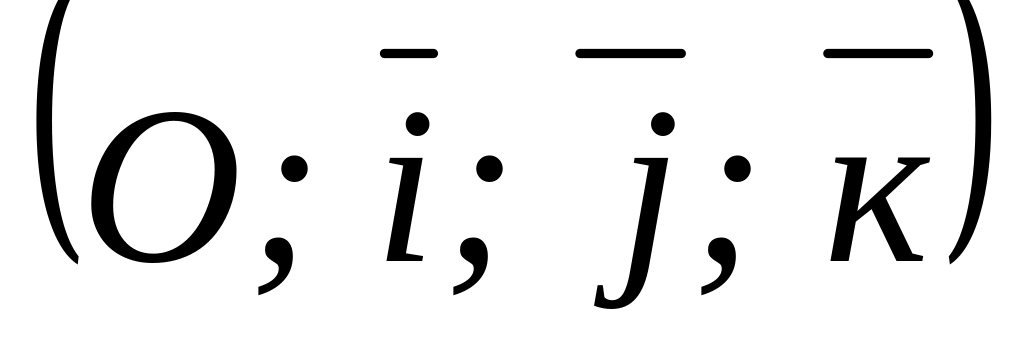.Построить радиус-векторы точек А (2; 1; 4); В ( 3; 2; 5); С (0; 0; 4).
Разложить радиус-векторы точек А ( 1; 4; 0); В (2; 2; 5); С (0; 3; 2) по ортам.
Определить координаты радиус-векторов точек М, К, L, E, H если:
.