18

Костромской энергетический техникум им. Ф.В. Чижова

Конспекты лекций по математике Тема: «Векторы на плоскости и в пространстве»

1. Понятие вектора

Векторы находят широкое применение в математике, физике, механике и других дисциплинах, упрощают вывод многих формул, решение многих задач, доказательство теорем.

Слово «вектор» происходит от латинского слова «vector»  переноситель, несущий.

Р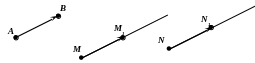 ассмотрим упорядоченную пару несовпадающих точек (А;В). Соединим точку А с точкой В и укажем направление от А к В. С помощью этой пары зададим преобразование плоскости (пространства). Каждой точке М плоскости (пространства) поставим в соответствие точку М₁ плоскости (пространства) (ее образ), которая получится в результате следующего построения: приняв точку М за начало, проводим луч т, одинаково направленный с лучом АВ. На луче т имеется единственная точка М₁, удаленная от точки М на расстояние, равное АВ.

Такое преобразование плоскости (пространства), определяемое упорядоченной парой точек называется «параллельным переносом» или «вектором».

Определение: Вектором или параллельным переносом, определяемым упорядоченной парой точек (А;В), называется преобразование плоскости (пространства), при котором каждая точка М плоскости (пространства) отображается на точку М₁ плоскости (пространства) так, что луч ММ₁ одинаково направлен с лучом АВ и расстояние ММ₁ равно расстоянию АВ.

Определение: Нулевым вектором называется вектор, начало которого совпадает с его концом. – нулевой вектор.

Вывод:

1. Любой ненулевой вектор задается упорядоченной парой несовпадающих точек.

2. Л юбой ненулевой вектор изображается направленным отрезком.

Обозначение:

А – начало вектора

В – конец вектора

Определение: Направлением ненулевого вектора называется направление луча АВ.

Определение: Длиной вектора (абсолютной величиной, модулем) называется расстояние между его началом и концом.

Определение: Вектор, длина которого равна единице, называется единичным вектором.

Вывод:

1. Любой ненулевой вектор характеризуется направлением и абсолютной величиной.

2. Длина нулевого вектора равна нулю, понятие направления не определено.

Определение: Два вектора называются одинаково направленными, если они имеют одинаковые направления. (Рис. 1)

Определение: Два вектора называются равными, если они имеют одинаковые направления и длины. (Рис. 3)

Рис. 1. Рис. 2. Рис. 3.

 и

и и и

одинаково направленные векторы равные векторы

векторы имеют одинаковую длину

Определение: Векторы, направления которых противоположны, называются противоположно направленными.

Определение: Векторы, направления которых противоположны, а длины равны, называются противоположными.

Замечание: Если и противоположные векторы, то пишут или .

Рис. 1. Рис. 2.

и |а| = |b|

и и

противоположно направленные противоположные векторы

векторы