Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский государственный университет им. Н.Г. Чернышевского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

РГР №3 «Вычисление и применение производных».doc

Скачиваний:

Добавлен:

01.07.2025

Размер:

1.5 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

ГБПОУ Региональный железнодорожный техникум

Расчетно-графическая работа №3

««Вычисление и применение производных и пределов»

по предмету

«Прикладная математика»

для групп 3-го курса специальности

08.02.10 «Строительство железных дорог, путь и путевое хозяйство»

Составлена

преподавателем

Орловой С.И

Брянск – 2017 г.

1. Вычислить пределы не используя правило Лопиталя (общая часть задания) Найдите пределы функции при , если:

Индивидуальные варианты

1	при , если	16	при , если
2	при , если	17	при , если
3	при , если	18	при , если
4	при , если	19	при , если
5	при , если	20	при , если
6	при , если	21	при , если
7	при , если	22	при , если
8	при , если	23	при , если
9	при , если	24	при , если
10	при , если	25	при , если
11	при , если	26	при , если
12	при , если	27	при , если
13	при , если	28	при , если
14	при , если	29	при , если
15	при , если	30	при , если

2. Вычислить пределы (можно использовать правило Лопиталя):

Вариант № 1

1) 2) ₃₎ ;

Вариант № 2

1) 2) ₃₎ ;

Вариант № 3

1) 2) ₃₎ ;

Вариант № 4

1) 2) ₃₎ ;

Вариант № 5

1) 2) 3)

Вариант № 6

1) 2) ₃₎ ;

Вариант № 7

1) 2) ; ₃₎

Вариант № 8

1) 2) ; 3)

Вариант № 9

1) 2) ; ₃₎ ;

Вариант № 10

₁₎2) ₃₎

Вариант № 11

1) 2) ₃₎ ;

Вариант № 12

1) 2) ₃₎

Вариант № 13

1) 2) ₃₎

Вариант № 14

₁₎ 2) ₃₎

Вариант № 15

1) 2) ₃₎

Вариант № 16

1) 2) ₃₎

Вариант № 17

1) 2) ₃₎

Вариант № 18

1) 2) ₃₎ ;

Вариант № 19

1) 2) ₃₎

Вариант № 20

1) 2) ₃₎

Вариант № 21

1) 2) ₃₎

Вариант № 22

1) 2) ; 3)

Вариант № 23

1) 2) ₃₎ ;

Вариант № 24

1) 2) ₃₎ ;

Вариант № 25

1) 2) ₃₎ ;

Вариант № 26

1) 2) ₃₎ ;

Вариант № 27

1) 2) 3) ;

Вариант № 28

1) 2) ₃₎ ;

Вариант №29

1) 2) ₃₎ ;

Вариант № 30

1) 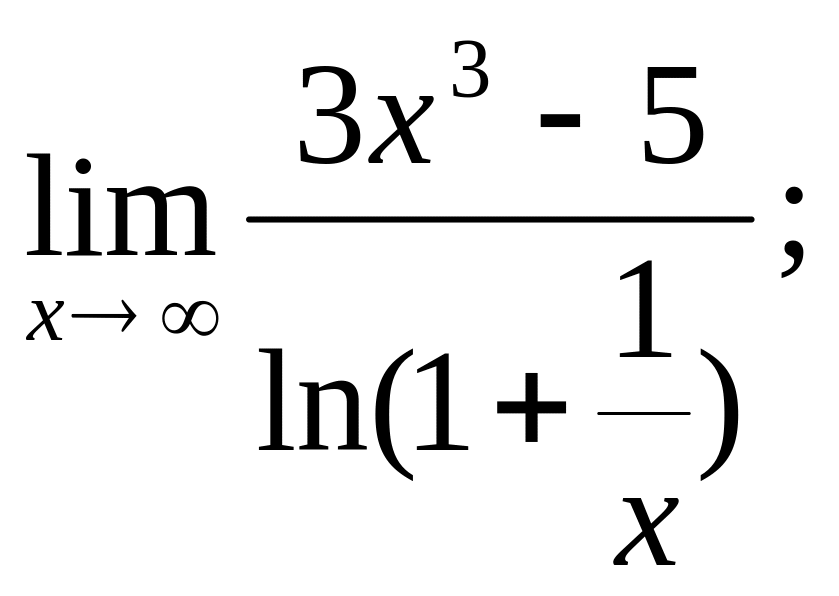2) ₃₎ ;

Вариант № 31

1) 2) ₃₎

Вариант № 32

1) 2) 3) .

3. . Найти производные первого порядка данных функций, используя правила вычисления производных.

1	а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) .	2	а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) .
3	а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з)	4	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .
5	а) ; в) ; д) ; ж) ; б) ; г) ; е) ; з) .	6	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .
7	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .	8	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з)
9	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .	10	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .
11	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .	12	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .
13	а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) .	14	а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) .
15	а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з)	16	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .
17	а) ; в) ; д) ; ж) ; б) ; г) ; е) ; з) .	18	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .
19	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .	20	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з)
21	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .	22	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .
23	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .	24	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .
25	а) ; б) ; в) ; д) ; ж) ; г) ; е) ; з) .	26	а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з)