Часть3. Остовные деревья графов. (Каркасы)

Рассмотрим произвольный связный граф (не дерево)

Остовным деревом (остовом, каркасом) называется суграф T(V,ET), являющийся деревом.

Каркас является частью графа (суграфом). Множество его вершин V(T)=V(G) совпадает с исходным графом

Построение минимальных остовов в нагруженных графах

Пусть нагруженный неориентированный граф с n вершинами, заданный матрицей весов .

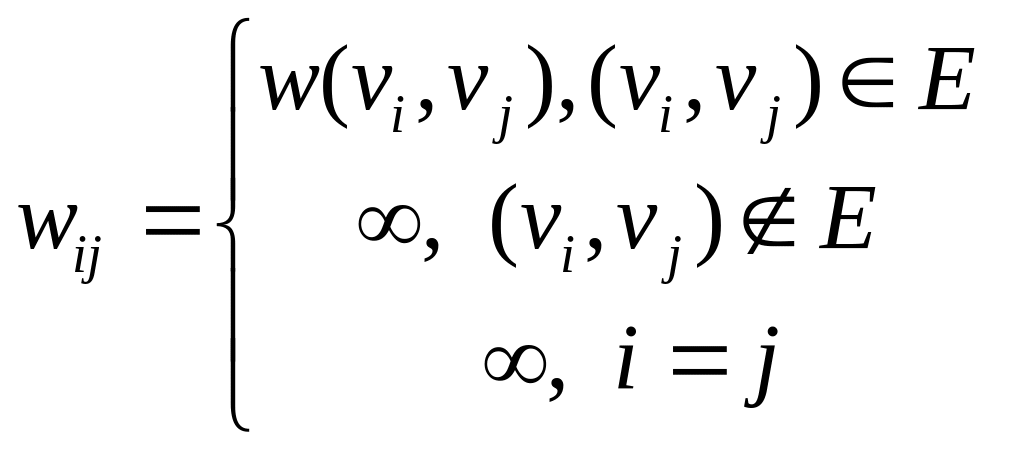
Как было определено ранее, остов это подграф, содержащий все вершины и являющийся деревом. Граф может иметь несколько различных остовов.

Суммарный вес остова равен сумме весов ребер, составляющих остов.

Возникает задача определения остовного дерева, имеющего минимальный суммарный вес.

Существуют различные алгоритмы построения минимального остова. Среди них известны алгоритм Краскала (жадный алгоритм) и алгоритм Прима (алгоритм ближайшего соседа).

Алгоритм Краскала (жадный алгоритм).

Идея алгоритма:

Остов графа строится последовательным объединением связных частей графа (компонент) путем добавления к ним ребра с минимальным весом. На начальном этапе граф представляет из себя n изолированных вершин, то есть n компонент связности. Множество ребер пусто. На каждом шаге прибавляем ребро из множества ребер не входящих в , которое имеет минимальный вес и не образует циклов с ребрами из . Добавляя ребра, мы каждый раз уменьшаем число компонент связности графа. Алгоритм продолжает работу, до тех пор пока число компонент связности не уменьшится до одной.

Шаг0. Определяем граф ,

- компоненты связности графа,

- множество еще не обработанных ребер графа.

Шаг1. Из множества не обработанных ребер выбираем ребро минимального веса

.

Шаг 2. Если вершины u и v принадлежат разным компонентам связности,, то добавляем ребро в множество ребер и объединяем рассматриваемые компоненты в одну.

.

Если число непустых компонент связности равно 1, то алгоритм заканчивает работу, иначе переходим к шагу 1.

Если вершины u и v принадлежат одной компоненте связности , то, то удаляем ребро из множества ребер , . Переходим к шагу 1.

Пример 3.1.

Решим задачу построения минимального остова с применением алгоритма Краскала для граф заданного на рис.3.1.

Рис.3.1. Исходный граф для решения задачи о минимальном остове.

1. На начальном этапе граф состоит из семи компонент связности.

, , , , , ,

Множество включает все ребра графа, множество пусто.

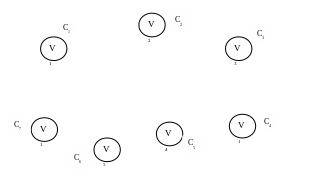
Рис. 3.2. Компоненты связности на начальном шаге алгоритма Краскала.

В качестве ребра с минимальным весом выбираем ,

Объединяем вершины и в одну компоненту связности

Компоненту связности удаляем. .

Рис. 3.3. Объединение компонент связности при добавлении ребра

Следующее ребро с минимальным весом

,

Компоненту связности удаляем.

Рис. 3.4. Объединение компонент связности при добавлении ребра

Следующее ребро с минимальным весом

,

Компоненту связности удаляем.

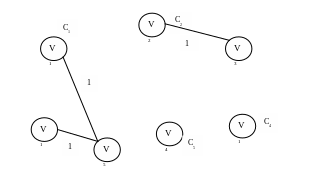
Рис. 3.5. Объединение компонент связности при добавлении ребра

Следующее добавляемое ребро имеет вес равный 2

,

Компоненту связности удаляем.

Рис. 3.6. Объединение компонент связности при добавлении ребра

Добавляем следующее ребро с минимальным весом

, . Получаем цикл. Значит его добавлять нельзя.

Следующее ребро с весом 2

,

Компоненту связности удаляем.

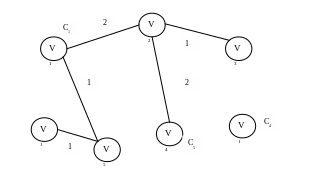
Рис.3.7. Объединение компонент связности при добавлении ребра .

Добавляем следующее ребро не образующее циклов

,

Компоненту связности удаляем.

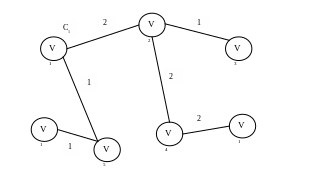
Рис .3.8. Конечное остовное дерево, полученное при добавлении ребра .

Так как компонента связности только одна, то алгоритм заканчивает работу.

Полученный в конечном итоге минимальный остов показан на рис 3.8

Суммарный вес равен 9

Результат работы может быть неоднозначным и зависит от порядка включения ребер. Можно получать различные остовы с одинаковым минимальным весом.

Пример 3.2. Работа алгоритма Краскала, в случае когда граф задан матрицей весов

Используем тот же граф, что и примере 3.1 граф

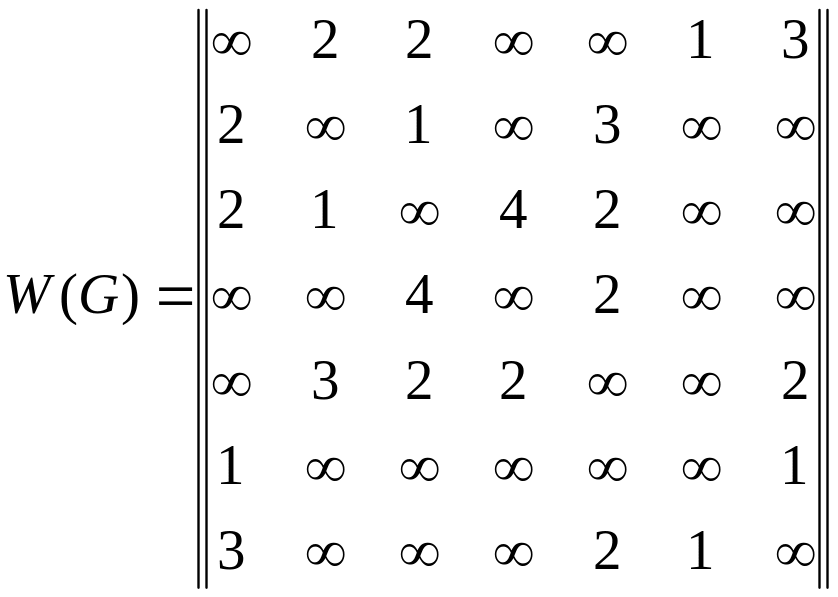
Выбираем первое ребро с минимальным весом равным 1 из первой строки матрицы.

Это ребро ,

Объединяем вершины и в одну компоненту связности

Следующее ребро с минимальным весом выбираем из второй строки матрицы

,

, . Компоненту связности удаляем.

Следующее ребро с минимальным весом находится в строке 6

,

Компоненту связности удаляем.

Следующее добавляемое ребро имеет вес равный 2 и находится в строке 1,

, .

, . Компоненту связности удаляем.

Добавляем следующее ребро с минимальным весом равным 2,

, . Получаем цикл. Значит его добавлять нельзя.

Следующее ребро с весом 2, не образующее цикла

, .

, . Компоненту связности удаляем.

Добавляем следующее ребро с весом 2, не образующее циклов,

, .

, . Компоненту связности удаляем.

Так как компонента связности только одна, то алгоритм заканчивает работу.

Получен тот же минимальный остов (см. рис 3.8.)

Суммарный вес равен 9

Алгоритм Прима (алгоритм ближайшего соседа).

Идея алгоритма:

На каждом шаге алгоритма будем формировать (достраивать) дерево следующим образом: к множеству ребер уже построенного дерева добавляем ребро минимального веса, один концов которого находится в множестве вершин предыдущего дерева , а другой в множестве , начиная с пустого дерева.

Шаг 0. .

Шаг 1. Выбираем в графе произвольную вершину u и инцидентное ей ребро (u,v ), имеющее минимальный вес.

.

Шаг 2. Из всех ребер, инцидентных вершинам текущего дерева, выбираем ребро минимального веса

Если (все вершины включены в каркас), то алгоритм заканчивает работу, иначе возвращаемся к шагу 2.

Пример 3.3.

Рассмотрим работ у алгоритма Прима, используя тот же исходный граф , что и в примерах 3.1 и 3.2.

На начальном этапе .

Возьмем в качестве начальной вершину 4.

Ребро с минимальным весом, инцидентное этой вершине,

,

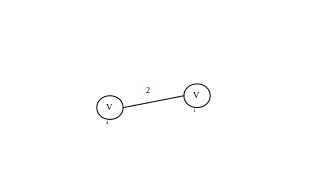
Рис. 3.9. Состояние текущего дерева, после добавления ребра .

Из ребер , инцидентных вершинам есть два ребра с минимальным весом равным 2. Это и . Выбираем ребро .

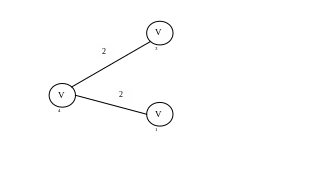
Рис. 3.10. Состояние текущего дерева, после добавления ребра

Следующее ребро определяется однозначно

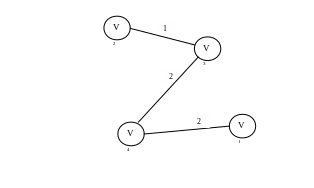
Рис. 3.11. Состояние текущего дерева, после добавления ребра

Из ребер , инцидентных вершинам выберем ребро с весом

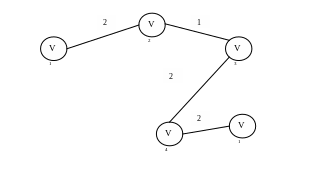
Рис. 3.12. Состояние текущего дерева, после добавления ребра

Следующее ребро с весом 1

Рис. 3.13 Состояние текущего дерева, после добавления ребра .

Последнее ребро с весом

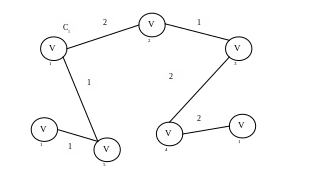
Рис. 3.14. Остов, полученный в результате работы алгоритма Прима