Министерство образования и науки Российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Ижевский государственный технический университет имени М.Т. Калашникова»

Т.Ю. Нистюк, к.т.н, доцент

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2

Алгоритмы работы в нагруженных графах

для студентов направления 11.03.02

« Инфокоммуникационные технологии и системы связи»

по дисциплине «Введение в теорию графов»

Ижевск Издательство ИжГТУ 2016

Теоретическая часть

Некоторые определения теории графов

В задачах и алгоритмах, связанных с поиском оптимальных маршрутов, обходом неориентированных графов используются такие понятия как маршрут, цепь, путь из вершины в вершину.

Незамкнутый маршрут – маршрут, состоящий из ребер, где каждые два соседних ребра имеют одну общую вершину (за исключением крайних ребер).

Цепь - незамкнутый маршрут, в котором нет повторяющихся ребер.

Простая цепь- цепь с неповторяющимися вершинами.

Расстояние от вершины до вершины – количество ребер в кратчайшей простой цепи из первой вершины во вторую.

В ориентированных графах, с учетом их особенностей , используются другие названия и термины.

Дуги, инцидентные данной вершине и имеющие направление от вершины называют исходящими, дуги, направленные к вершине входящими.

Путь (ориентированный маршрут)-последовательность дуг , в которой конечная вершина одной дуги является начальной вершиной следующей(за исключением быть может крайних)

Цепь - незамкнутый путь в котором все дуги различны.

Простая цепь-цепь, в которой все вершины попарно различны.

Часть1. Задача о поиске кратчайшего пути из одной вершины в другую вершину графа.

Рассмотрим часто встречающуюся задачу, связанную с поиском маршрутов и путей в графах: задачу о поиске минимального пути и алгоритм ее решения.

Пусть необходимо найти минимальный путь из некоторой вершины в другую вершину .

Ниже приводится один из алгоритмов решения задачи

Алгоритм поиска путей с минимальным числом ребер (дуг) для графов .

Алгоритм работает как для неориентированных так и орграфов.

Идея алгоритма:

Пусть -граф с числом вершин .

Минимальный путь находим, последовательно просматривая сначала множество вершин, смежных с начальной вершиной (помечая их индексом ). Затем просматриваем все вершины, смежные с вершинами первого уровня, исключая при этом ранее пройденные (помеченные) вершины, и присваиваем оставшимся вершинам индекс . И так далее, до тех пор, пока не встретим конечную вершину .На каждом уровне получим множество вершин находящихся на одинаковом расстоянии от начальной вершины. Индекс определяет длину минимального пути для вершин данного уровня от вершины .

В конечном итоге, имея такую информацию, можно определить все простые пути, связывающие начальную и конечную вершины, содержащие минимальное число дуг. На каждом уровне можно дополнительно построить граф минимальных путей из начальной вершины в вершины данного уровня. В конце этот граф должен содержать все кратчайшие пути от начальной вершины до конечной вершины .

Описание алгоритма

Шаг 1. Помечаем вершину индексом , а окрестность , состоящую из вершин исходящих дуг индексом .

Множество вершин с индексом обозначим .

Шаг 2. Анализируем множество . Если или , то вершина не достижима из вершины , идем на конец. (шаг 6.)

Шаг 3. Проверяем наличие последней вершины во множестве , если , то минимальный путь найден, иначе к шагу 4.

Шаг 4. Помечаем индексом все непомеченные вершины, являющиеся концами дуг, исходящих из вершин множества . Получаем множество .

Шаг 5. Присваиваем , переход к шагу 2.

Шаг 6. Конец алгоритма.

Рассмотрим работу алгоритма на примере орграфа (рис.1.1).

Пример 1.1.

Рис 1.1. Орграф с n=8, m=13

Найдем все кратчайшие пути из вершины 1 в вершину 8.

Шаг 1. , .

Переходим в шагу 1. На первом этапе, рассматривая окрестность вершины 1, получаем множество .

Поскольку множество не пусто и индекс переходим к следующему уровню.

На втором уровне определяем непомеченные ранее вершины, которые являются концами исходящих из вершин 2 и 3 дуг, получаем множество .

На третьем уровне – множество . Множество содержит конечную вершину. Длина минимального пути равна 3.

Рассмотрим работу алгоритма в случае, если граф задан матрицей смежности. Дополнительно построим на каждом уровне граф минимальных путей из начальной вершины в вершины с индексом .

Для графа (рис. 1) матрица смежности равна

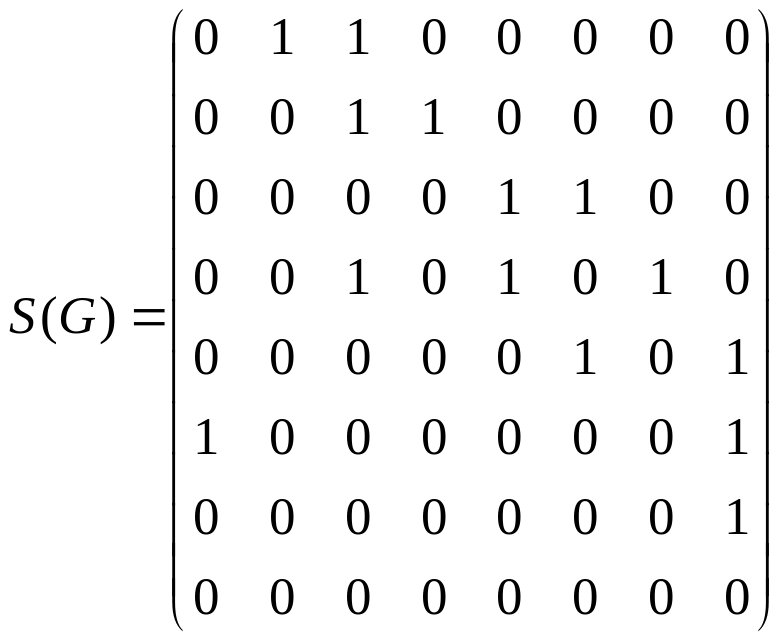
Просматриваем строку матрицы смежности, соответствующую начальной вершине 1. По ней строим окрестность начальной вершины. .

Рис.1.2. Граф минимальных путей для вершин первого уровня.

На следующем этапе рассматриваем строки для вершин 2 и 3. Включаем в множество вершины, которые являются концами дуг, исходящих из этих вершин, не помеченные ранее. Получаем множество вершин , .

Граф минимальных путей на данном этапе

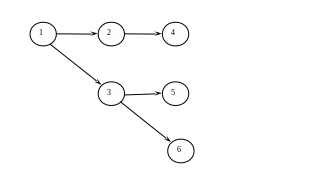
Рис. 1.3. Граф минимальных путей для вершин второго уровня

Затем для вершин 4, 5, 6 аналогичным образом получаем множество вершин

Граф возможных кратчайших путей до вершин третьего уровня 7 и 8.

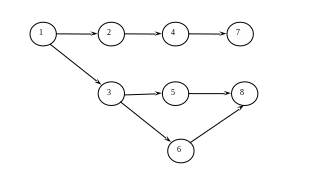
Рис. 1.4. Граф минимальных путей для вершин 3-го уровня.

Пути до конечной вершины найдены.

1→3→5→8

1→3→6→8