
- •3.6.Разложение логических функций по переменным. Совершенные нормальные формы.
- •Примеры 3.14.Какие из ниже перечисленных формул являются, а какие не являются кнф:
- •Примеры 3.15.Какие из ниже перечисленных формул являются, а какие не являются днф:
- •Пример 3.19. Какие из ниже перечисленных формул являются, а какие не являются скнф:
- •Пример 3.17.Какие из ниже перечисленных формул являются, а какие не являются сднф:
- •Построение сднф и скнф по таблице истинности. Правило построения скнф по таблице истинности.
- •Правило построения сднф по таблице истинности.
- •3.7.Двойственность.
- •Глава 4.Приложения алгебры логики в технике.
- •4.1. Приложение алгебры высказываний к релейно-контактным схемам (ркс).
- •4.2. Решение логических задач с помощью алгебры логики.
3.6.Разложение логических функций по переменным. Совершенные нормальные формы.
Для любой формулы алгебры высказываний можно указать равносильную ей формулу, содержащую лишь три основные операции: отрицание, дизъюнкция, конъюнкция.
Например,
импликация и эквиваленция легко
выражаются через отрицание, дизъюнкцию
и конъюнкцию:
 ,
,
 .
.
Пример
3.13.
Преобразовать формулу
 так,
чтобы она содержала лишь три основные
операции:
так,
чтобы она содержала лишь три основные
операции:

Решение.
Используя
равносильные преобразования, имеем: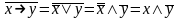 .
.
Выразить
данную формулу через отрицание, конъюнкцию
и дизъюнкцию возможно не одним способом,
а многими. К примеру, рассматриваемая
в примере формула равносильна также
следующим формулам, содержащим из
логических связок лишь 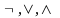 :
:
 и
так далее.
и
так далее.
Среди всевозможных выражений данной формулы через конъюнкцию, дизъюнкцию и отрицание некоторые играют важную роль, как в алгебре высказываний, так и в ее приложениях. Рассмотрение таких выражений, называемых совершенными нормальными формами, и составляет цель настоящего параграфа.
Нормальная форма логической формулы не содержит импликации, эквиваленции и отрицания не элементарных формул.
Нормальная форма существует в двух видах:
1) Конъюнктивная нормальная форма (КНФ) - это формула, имеющая вид конъюнкций нескольких(или одного) элементарных дизъюнкций.
Элементарными дизъюнкциями называются дизъюнкции переменных, в которых каждая переменная или ее отрицание встречается не более одного раза.
Например,
 -
элементарные (простые) дизъюнкты,
-
элементарные (простые) дизъюнкты,
 -
конъюнкция
двух элементарных дизъюнкций, то есть
конъюнктивная нормальная форма.
-
конъюнкция
двух элементарных дизъюнкций, то есть
конъюнктивная нормальная форма.
Примеры 3.14.Какие из ниже перечисленных формул являются, а какие не являются кнф:
1) ;2)
;2) ;
3)
;
3)
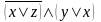 ;4)
;4)
 ;5)
;5)
Решение.
Третья формула не является КНФ, так как отрицание в первой скобке расположено не над переменной, а над сложным выражением (высказыванием). Четвертая формула не являются КНФ, так как не является конъюнкцией элементарных дизъюнкций. Все остальные примеры являются элементарными конъюнкциями.
2)Дизъюнктивная нормальная форма (ДНФ) - эта формула, имеющая вид дизъюнкций элементарных конъюнкций.
Элементарными конъюнкциями называются конъюнкции переменных, в которых каждая переменная или ее отрицание встречается не более одного раза.
Например,
 -
элементарные (простые) конъюнкты,
-
элементарные (простые) конъюнкты,
 -
дизъюнкция
двух элементарных конъюнкций, то есть
дизъюнктивная нормальная форма (ДНФ).
-
дизъюнкция
двух элементарных конъюнкций, то есть
дизъюнктивная нормальная форма (ДНФ).
Замечание:
Примеры 3.15.Какие из ниже перечисленных формул являются, а какие не являются днф:
1)
 ;2)
;2)
 ;3)
;3)
 ;4)
;4)
 ;5)
;5)
 ;6)
;6)
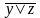 ;7)
;7)
 .
.
Решение.
Третья формула не является ДНФ, так как в ДНФ перемножаются лишь переменные или их отрицания. Шестая не является ДНФ, так как в ДНФ отрицание может располагаться лишь над переменными ,а здесь отрицание располагается над логической операцией. Остальные формулы являются дизъюнктивными нормальными формами. При этом седьмая формула является одновременно ДНФ и КНФ.
Алгоритм приведения формулы к ДНФ:
1. Выразить все логические операции в формуле через дизъюнкцию, конъюнкцию и отрицание.
2. Используя, законы де Моргана, переносят все отрицания к переменным и сокращают двойные отрицания.
3. Используют закон дистрибутивности конъюнкции относительно дизъюнкции, преобразуют формулу так, чтобы все конъюнкции встречались раньше дизъюнкции.
Алгоритм приведения к КНФ аналогичен, только на шаге 3 делают так, чтобы все дизъюнкции встречались раньше конъюнкции.
Пример
3.16. Привести
к KНФ формулу: а)
 ;
б)
;
б)
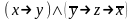 .
.
Решение.
а)
Приведём к КНФ данную формулу
для этого уберем отрицания не элементарных
дизъюнкций используя закон де Моргана:
 - КНФ;
- КНФ;
б)
Для
этого заменим
 на
на
 ,
используя
формулу
,затем
применяем закон де
Моргана и закон дистрибутивности
дизъюнкции относительно конъюнкции:
,
используя
формулу
,затем
применяем закон де
Моргана и закон дистрибутивности
дизъюнкции относительно конъюнкции:

Пример
3.17. Привести
к ДНФ формулу: а)
 ;
б)
;
б)
 .
.
Решение.
а)
Приведём
к ДНФ данную формулу
для этого уберем отрицания не элементарных
конъюнкций используя закон де Моргана
и
закон дистрибутивности конъюнкции
относительно дизъюнкции:
 ДНФ;
ДНФ;
б)
Учитывая,что
и
 имеем:
имеем:

Очевидно, что каждая формула имеет бесконечно много ДНФ и КНФ.
Пример 3.18. Найдем
несколько ДНФ для формулы
 .
.
Решение.
1)

3)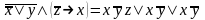 ;
;
4)  и
так далее.
и
так далее.
Совершенная конъюнктивная нормальная форма (СКНФ) - это КНФ, удовлетворяющая четырем условиям:
1) различны все члены конъюнкции;
2) различны все члены каждой дизъюнкции;
3) ни одна дизъюнкция не содержит переменную вместе с отрицанием этой переменной;
4) каждая дизъюнкция содержит все переменные, входящие в исходную формулу.
