Цель работы:
- изучение программного продукта MatLab как инструмента по цифровой обработке сигналов;
- синтез цифрового фильтра с заданным АЧХ;
- ввод информации с аудио файла и его цифровая обработка (фильтрация, получение спектральной плотности с помощью ДПФ или БПФ, модуляция);
- получение спектрограмм модулированных сигналов.
Ход работы:
Запустить программу MatLab.
Пример окна запуска версии MatLab 7.11.0.
По варианту задания произвести считывание аудио-файла в MatLab.
Для считывания, аудио-файл должен располагаться в рабочем каталоге MatLab, – например, …\ \work\test.wav, где test.wav – тестовый аудио файл (запись моно, 16 разрядов, 8 кГц, 10000 отсчетов). Установить в строке «Current folder» рабочий каталог и выполнить считывание:
>> hfile = 'test.wav';
>> y=wavread (hfile);
или одной командой
>> y=wavread ('test.wav');
возможно считывание следующими командами:
>> hfile = 'test.wav';
>> [y, Fs, bits]=wavread (hfile) ;
или одной командой
>> [y, Fs, bits]=wavread ('test.wav');
где Fs вернет значение частоты дискретизации, bits – количество бит для одного отсчета.
Произвести просмотр файла можно с использованием окна по команде:
>> sptool;
Для просмотра файла необходимо выполнить Файл -> Импорт… (File -> Import…)
В окне:
необходимо выбрать y; нажать на кнопку для поля «Данные» («Data») и установить 8000 для поля «Частота выборки» («Sampling Frequency»).
Затем нажать «Ок». В окне SPTool «Сигналы» («Signals») выбрать sig1[vector] и нажать «Вид» («View») под окном редактирования «Сигналы» («Signals»).
В результате на экране появится временной график сигнала, считанного из файла test.wav.
Закрыть окно графика и SPTool, не сохраняя сессию.
2. По варианту задания произведем синтез полосового фильтра.
Для синтеза стандартных фильтров можно использовать:
- butter(n, w0, type) – расчет фильтров Баттерворта;
- cheby1(n, Rp, w0, type) – расчет фильтров Чебышева первого рода;
- cheby2(n, Rp, w0, type) – расчет фильтров Чебышева второго рода;
- ellip(n, Rp, Rs, w0, type) – расчет фильтров Кауэра;
где n – порядок фильтра, Rp и Rs – уровень пульсаций АЧХ в полосе пропускания и задержания (дБ), w0 и type – тип фильтра:
ФНЧ – w0 – скаляр; type – нет; (фильтр низких частот);
ФВЧ – w0 – скаляр; type – ‘high’; (фильтр высоких частот);
ПФ – w0 – двухэлементный вектор [w1 w2]; type – нет; (полосовой фильтр);
РФ – w0 – двухэлементный вектор [w1 w2]; type – ‘stop’; (режекторный фильтр).
В зависимости от количества возвращаемых параметров формируются формы цифровых фильтров:
[b, a]= - коэффициенты рекурсивной и нерекурсивной части цифрового фильтра (числителя и знаменателя функции передачи);
[z, p, k]= - нули и полюса;
[A, B, C, D]= - параметры пространства состояний.
Минимальный порядок фильтра можно вычислить, используя функции:
[n, Wn]= buttord(Wp, Ws, Rp, Rs)
[n, Wn]= cheby1ord(Wp, Ws, Rp, Rs)
[n, Wn]= cheby2ord(Wp, Ws, Rp, Rs)
[n, Wn]= ellipord(Wp, Ws, Rp, Rs)
где Wp и Ws – задают границы полос пропускания и задержания (нормированные к частоте Найквиста):
ФНЧ – Wp<Ws;
ФВЧ – Wp>Ws;
ПФ – Ws(1)< Wp(1)<Wp(2)<Ws(2);
РФ - Wp(1)< Ws(1)<Ws(2)<Wp(2).
Пусть для сигнала test.wav необходимо синтезировать ПФ с частотой среза 0,7 кГц и 2,1 кгц; с неравномерностью АЧХ 1 дБ; скоростью нарастания затухания 0,2 дБ/Гц; с затуханием в полосе непропускания 60 дБ.
Получим модель АЧХ (по затуханию), шкала частот в килогерцах и нормированная шкала:
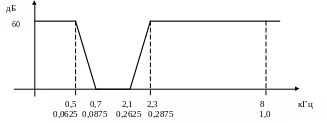
>> Ws = [0.0625 0.2875];
>> Wp = [0.0875 0.2625];
>> Rp = 1;
>> Rs = 60; (K=0.001)
>> [n, Wn]= ellipord(Wp, Ws, Rp, Rs);
Для полученных значений параметров синтезируем фильтр командой:
>> [b, a] = ellip(n, Rp, Rs, Wn);
Для получения АЧХ и ФЧХ в логарифмической шкале можно выполнить:
>> freqz(b, a);
>> plot(w, abs(h));
Выводится график.
>> grid on;
Формируется сетка.
или АХЧ в линейном масштабе:
>> [h, w]=freqz(b, a);
>> plot(w, abs(h));
Выводится график.
>> grid on;
Формируется сетка.
или АХЧ в децибелах:
>> [h, w]=freqz(b, a);
>> plot(w, 20*log10(abs(h)));
Получим график АЧХ:
Для получения сетки на графике АЧХ, в главном окне выполним команду:
>> grid on;
Как видно с АЧХ полосовой фильтр получился с заданными параметрами.
Выполнить закрытие окна с графиком АЧХ.
Для сравнения можно получить коэффициенты рекурсивного фильтра по кусочно-линейной АЧХ строкой вида, после задания параметров для синтеза фильтра (n, f, m):
>> [b, a] = yulewalk(n, f, m);
где a и b - коэффициенты рекурсивной и нерекурсивной части цифрового фильтра; n – порядок фильтра; f – значения нормированных частот и m – значения затухания для соответствующих точек частот.
Вектора a и b будут иметь размерность n+1.
Пример синтеза фильтра по кусочно-линейной АЧХ (для получения численных значений используем соответствующие точки графика, см. выше):
>> f = [0 0.0625 0.0875 0.2625 0.2875 1];
>> m = [0.001 0.001 1 1 0.001 0.001]; (A=60 дБ – уровень затухания на графике)
>> nl = 51;
>> [b, a] = yulewalk(nl, f, m);
Для получения синтезируемого АЧХ выполним (по оси Y коэффициент передачи):
>> plot(f,m);
Для получения АХЧ в децибелах выполним:
>> [h, w]=freqz(b, a);
>> plot(w/pi, 20*log10(abs(h)));
Как видно по АЧХ синтез фильтра был выполнен успешно.
3. Выполним фильтрацию загруженного в вектор y сигнала с файла test.wav.
>> y1=filter(b, a, y);
Для просмотра результатов в визуальной форме выполним:
>> sptool;
дальнейшие действия в окне SPTool выполняем по аналогии действий пункта 1 для массива y1, вместо y. В результате получим график вида:
Как видно форма сигнала значительно изменилась.
Закрыть все активные окна, кроме основного окна программы MatLab.
4. Получим спектральную плотность сигнала для различных временных участков.
Для различных вариантов задания выбрать три различные временные точки для анализа.
Для нашего примера, выберем две начальные временные точки t1=0,12сек и t2=0,25сек, для обработки используем 512 отсчетов сигнала (кратное степени 2).
Для нашего файла Fs=8000 и bits=16, тогда
для t1: N0=8000*0,12=960;
для t2: N1=8000*0,25=2000.
Выполним команды для временной точки t1:
>> nt=960;
>> Y=fft(y(nt:nt+512),512);
>> Pyy=Y.*conj(Y)/512;
>> f=8000*(1:256)/512;
>> plot(2*f, Pyy(1:256));
Выполним команды для временной точки t2:
>> nt=2000;
>> Y=fft(y(nt:nt+512),512);
>> Pyy=Y.*conj(Y)/512;
>> f=8000*(1:256)/512;
>> plot(2*f, Pyy(1:256));
Как видно из графиков спектр для точки t2 не имеет ярко выраженных спектральных «всплесков» (формант) по сравнению со спектром для точки t1.
Получим для сравнения спектры сигнала в этих точках после прохождения сигнала через полосовой фильтр (ellip), массив y1:
>> nt=960;
>> Y=fft(y1(nt:nt+512),512);
>> Pyy=Y.*conj(Y)/512;
>> f=8000*(1:256)/512;
>> plot(2*f, Pyy(1:256));
И для nt=2000:
>> nt=2000;
>> Y=fft(y1(nt:nt+512),512);
>> Pyy=Y.*conj(Y)/512;
>> f=8000*(1:256)/512;
>> plot(2*f, Pyy(1:256));
Как видно из графиков АЧХ фильтром, осуществлено выделение частот в полосе пропускания полосового фильтра, и их подавление вне пропускания полосового фильтра.
Главное окно после ранее выполненных операций имеет вид:
