
Тест_10 класс (переходный)
.docxТест 10 класс (математика)
№ 1 Наименьшее целое решение неравенства 2х + 3 > 5:
а) 1 б) 14 в) 2 г) 0,5
№2. Сколько нулей имеет функция у = х2 – х?
а) 4 б) 1 в) 2 г) 5
№ 3 Выберите верное утверждение
1) cos2a – 1 = - sin2 a 2) sin2 a = cos2 a - 1
3) sin2 a - cos2 a = 1 4) tg( π – a ) = ctg a
№ 4 Известно, что 0< a < π/2. Найдите sin a, если cos a = 3/5
1) -4/5 2) 4/5 3) 3/5 4) -3/5
№ 5. При каких значениях у трехчлен 2у2 – 3у – 2 принимает положительные значения?
1) (-1/2; 2) 2) ( -∞; -1/2] и [ 2 ; ∞ )
3) [ -1/2; 2 ] 4) ( -∞; -1/2) и ( 2 ; ∞ )
у
= х2
№ 6 Из данных уравнений подберите второе уравнение системы так, чтобы она имела два решения ( используйте графическое …….
представление).
1) у = х – 1 2) у = -х -1 3) у = 1/х 4) у2 + х2 = 1
№7 В зрительном зале 450 мест. В партере – 24% всех мест, а остальные места - в амфитеатре. Сколько мест в амфитеатре?
а) 342 б) 108 в) 426 г) 302
№
8 Найдите сумму корней уравнения

1) 2 2) 11 3) 8 4) 0
№ 9 Из арифметических прогрессий выберите ту, среди членов которой есть число 5.
1) аn = 5n + 1 2) аn = 5n -1 3) аn = 5n 4) аn = - 5n + 1
№ 10 Упростить выражение: - 3 sin2 a + 7 - 3 cos2 a
1) 4 – cos2 a 2) 4 3) cos2 a 4) - cos2 a
№
11 Решить неравенство:

1) ( -∞; -3] и [ 8; ∞ ) 2) [ -3; -2)и [ 8; ∞ )
3) (- 2 ;8] 4) [ - 3; ∞ )
№12 Вычислить

1) 18 2) 12 3) 6 4)36
№
13 Найдите tg a,
если cos a =
 и
и

1)0,5 2) 2 3) - 2 4) – 0,5
№
14 Вычислить выражение:
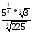
1)
 2)
2)
 3)
3)
 4)
4)

№ 15 Какая из перечисленных ниже пар чисел является решением системы уравнений

1) ( 4; 1) 2) ( 2; 3) 3) ( -4; 3) 4) ( 4; -2)
№ 16 Найдите значение выражения
 -7
-7 .
.
1) 17 2) 0,8 3)
 4) 4
4) 4
№17 Выразите из формулы k2=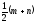 переменную n.
переменную n.
1) n=k2+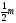 2) n=2k2+m
3) n=
2) n=2k2+m
3) n= 4) n=2k2-m
4) n=2k2-m
№18. Выполните умножение
 .
.
1)
 2)
2)
 3) -
3) - 4) -
4) -
№19. Решите неравенство 3(x-2) - 5(x+3) > x.
1)
 2)
2)
 3)
3)
 4)
4)

№20 Упростите выражение
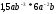 .
.
1)
 2)
2)
 3)
3)
 4) 9ab2
4) 9ab2
№21 Запишите в стандартном виде число 52 000 000.
1) 52*106 2) 0,52*108 3) 5,2*107 4) 5,2*10-7
№22
Найдите наименьшее целое число y
из области определения выражения
 . 1) 0 2) -1
3) -4 4) 1
. 1) 0 2) -1
3) -4 4) 1
№23 Найдите количество точек
пересечения графиков функций
 и у = -3х
и у = -3х
1) 0 2) 2 3) 1 4) ни одной
№24 Наименьшее целое решение неравенства 2х + 3 > 5:
а) 1 б) 14 в) 2 г) 0,5
№25 Решите систему неравенств.

1) [0; 7 ) 2) [1; 7 ) 3) [0; -7) 4) [5; 7 )
№27. Вычислить

1)
 2)
2)
 3)
3)
 4)
4)

№ 28. Укажите уравнение, которое не имеет корней.
1) 9,1 х2 + 4,5 = 0 2) 9,1 х2 + 4,5х = 0
3) 9,1 х2 - 4,5 = 0 4) 9,1 х2 - 4,5х = 0
№ 29 Решите уравнение ( 3х – 1)(х + 4) = х2 - 3х – 4. Если корней несколько, найди те их среднее арифметическое.
1) 0 2) нет корней 3) – 7 4) – 3,5
№ 30 Какая из данных прямых имеет две общие точки с параболой у = - х2 – 3?
1) у = - 4 2) у = -3 3) у = 2 4) у = 5
№
31 Сколько решений имеет система
уравнений

1) 1 2) 2 3) 3 4) ни одного
№ 32 Укажите уравнение, которое не имеет корней.
1) 9,1 х2 + 4,5 = 0 2) 9,1 х2 + 4,5х = 0
3) 9,1 х2 - 4,5 = 0 4) 9,1 х2 - 4,5х = 0
№ 33 В треугольнике АВС АD биссектриса, угол С равен 210, угол САD равен 300. Найдите угол В. Ответ дайте в градусах.
1) 900 2) 700 3) 990 4) 500
№
34 Записать числа в порядке убывания
 ;
0,3999; 0,55;
;
0,3999; 0,55;

1)
0,3999; 0,55;
 ;
;
 ; 2)
; 2)
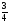 ;
0,55;
;
0,55;
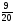 ;
0,3999;
;
0,3999;
3)
 ;
0,3999; 0,55;
;
0,3999; 0,55;
 ; 4)
0,55; 0,3999;
; 4)
0,55; 0,3999;
 ;
;
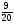 ;
;
№ 35 По заданной формуле n-го члена последовательности аn = -3n + 7
вычислить аn при n = 4
1) 19 2) 5 3) 7 4) -5
№ 36 Найти выражение, значение которого равно 0
1) (-1)4 + (-1)5; 2) (-1)5 - (-1)4; 3) -14 * (-1)5; 4) – 15 : (-1)3.
.№ 37 Не выполняя построения, найдите координаты точки пересечения графиков функций у = х5 – 2 и у = 30.
1) (-2; 2) 2) (-2; -30) 3) (2; 30) 4) (32;2).
№38 Определите, какая из функций является возрастающей на всей области определения.
1) у
= х4 -1 2) у = -5х – 2 3)
 4)
у = х9
4)
у = х9
№ 39. Найдите область значений функции у = 5 cos х + 1
1) [ -5; 5 ] 2) [ -4; 6 ] 3) [ -6; 6 ] 4) [ 1; 2 ]
№
40 Известно, что π/2<
a < π.
Найдите cos a, если
sin a =
 .
.
1) 8/17 2) -8/17 3) 64/17 4) -64/17
.№ 41 При каких значениях у трехчлен 3у2 + 8у – 3 принимает отрицательные значения?
1) [ -3; 1/3 ] 2) ( -∞; -3]
3) (-3; 1/3) 4) ( -∞; -3) и ( 1/3 ; ∞ )
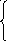
№ 42 Из данных уравнений подберите второе уравнение системы y = - x2 так, чтобы она имела два решения ( используйте графическое ……..
представление).
1) у2 + х2 = 4 2) у = х +1 3) у = 1/х 4) у = - х +1
№ 43 Из арифметических прогрессий выберите ту, среди членов которой есть число 4.
1) аn = 4n - 1 2) аn = 4n +1 3) аn = -4n 4) аn = 4 n
№ 44 Какой угол (в градусах) описывает минутная стрелка за 10 мин?
1)100 2) 600 3) 150 4) 450
№45
Решить неравенство:

1) ( -∞; -3] и (- 2 ;8] 2) [ -3; -2)и ( 2; 8]
3) [ 8; ∞ ) 4) [ - 3; ∞ )
№46
Вычислить

1) 18 2) 6 3) 12 4) 36
.№
47 Найдите tg a,
если sin a =
- и
и

-
0,5 2) 2 3) -2 4) – 0,5
№ 48 Вычислить выражение: - 15 * 811/4 - 19
1) 26 2) 116 3) - 64 4) - 154
№ 49 Какая из перечисленных ниже пар чисел является решением системы уравнений

1) ( 4; 1) 2) ( 5; 2) 3) ( -4; 3) 4) ( 2; 3)
№ 50 Какая из данных прямых не имеет общих точек с параболой у = - х2 + 3?
1) у = 4 2) у = 3 3) у = 2 4) у = 0
№
51 Сколько решений имеет система
уравнений

1) 1 2) 2 3) 3 4) ни одного
№ 52
№53
Вычислить

1) 2,85 2) 35,8 3) 5,85 4) - 5
№ 54 Каким будет следующий член геометрической прогрессии 2; -12; 72; …?
1) -432 2) 216 3) -542 4) 432
№ 55 Какое из приведенных ниже выражений тождественно равно произведению
(х-4)(х-2)?
1) (х-4)(2-х); 2) –(4-х)(2-х); 3) –(4-х)(х-2); 4) -(4-х)(2-х).
№ 56. Не выполняя построения, найдите координаты точек пересечения графиков функций у = х3 – 2 и у = 6.
1) (2; 6) 2) (-2; 8) 3) (2; -2) 4) (8; 2).
№ 57. Определите, какая из функций является убывающей на всей области определения.
1)
у = х4 -1 2) у = -5х – 2 3)
 4) у = х9
4) у = х9
№
58. Решите неравенство: 3х + 9
 6(х – 1).
6(х – 1).
а) х б) х
б) х
 5
в) х
5
в) х -5
-5
№59. Укажите выражение, в область определения которого входит число 4.
а)
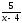 б) х
б) х в)
в)

№60.
Решите систему
неравенств:

а) х
 4 б) х
4 б) х
 - 8 в) -8
- 8 в) -8
 х
х
 2
2
№
61 Укажите наименьшее
целое решение системы неравенств:

а) 4 б) 5 в) 10
№
62 При каких значениях
переменной имеет смысл выражение:
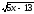
а) х > 2,6 б) х
 в) х > -2,6
в) х > -2,6
№ 63 Если а > b, то а – b = -7
а) да б) нет в) не знаю
№ 64 Значение какого из данных выражений положительно, если известно, что х > 0,
у < 0?
а) ху б) (х – у)х в) (х – у)у
№
65 Решите уравнения:

а) 3 б) нет корней в) -3; 3
№
66 Найдите сумму и
произведение корней уравнения:
х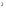 -
10х + 9 = 0
-
10х + 9 = 0
а) х =
10, б) х
=
10, б) х =
10, в) х
=
10, в) х =
-10,
=
-10,
х =
9 х
=
9 х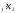 =
-9 х
=
-9 х =
9
=
9
№
67 Сократите дробь:

а) 3 б) в)
в)

№
68 Проверьте, верно ли
выполнены действия:

а) да б) нет в) не знаю
№
69 Упростить выражение:

а) sin2x б) cos2x в) 1 с) 0
№70 Найти значение выражения cos 450(cos 250sin700 – cos700sin 250)
а) 1 б) 0,75 в) 0,5 г) 0
№
71 Вычислите:

а)
 ;
б)1; в)
;
б)1; в)
 ;
г) -1
;
г) -1
№
72. Решите уравнение:

1)
 , k
, k
 Z,
3)
Z,
3)
 2)
2)
 , k
, k
 Z,
4)
Z,
4)
 ,
,
 ,
,
 №
73. Решите неравенство:
№
73. Решите неравенство:

1)
 2)
2)
 3)
3)
 4)
4)
№ 74 Раствор содержит 5 % соли. Сколько граммов соли содержится в 220 г такого
раствора?
а) 44; б)110; в) 11; г) 1,1.
№
75 Найдите значение суммы хо
+ уо , если известно, что ( хо;
уо) – решение системы уравнений


а) 3; б) 1; в) 2; г) 0.
№ 76. По графику функции, изображенному на рисунке, определите промежуток, в котором значения функции отрицательны.
а) [- 4; 4]; б) [ - 4; 0) в) ( - 4; 4 ) ; г) [ - 4; 0 ].
№77. Упростите выражение ( х + 3 ) ( х – 3 ) – х ( х – 2 ).
1) 2х + 9; 2) – 2х – 9; 3) – 2х + 9; 4) 2х – 9.
№ 78. При каком а равенство 4(2z - 3) + 6(z - 2) = az – 24 является тождеством?
а) - 8 б) 14 в) 12 г) другой ответ
№ 79. Найти значение выражения:

1) 13 2) 129 3) 258 4) -15
№ 80. Дано: sina = 0,28,
 .
Найти sin 2a
.
Найти sin 2a
1)
 2)
2)
 3) 4,25 4) 0,136
3) 4,25 4) 0,136
№ 81. Некоторая фирма производит установку электроплит в квартирах. Прогноз показал, что за первый месяц сотрудники фирмы установят 300 плит, а каждый последующий месяц количество заказов будет возрастать на 100.За сколько месяцев будет установлено 15000 электроплит?
1) 15 месяцев 2) 2 месяца 3) 8 месяцев 4) 24 месяца
№ 82. Упростить выражение

1) 25 -16
2) 25 - 4
-16
2) 25 - 4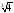 3) 19 4) 5
3) 19 4) 5
№ 83. Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей, после повышения цены на 10%?
1) 20 2) 18 3) 21 4) 24
№ 84. Найти множество значений функции f(x) = -5cosx
1) [ -1; 1] 2) [ 1; 5] 3) [ -5; 1] 4) [ -5; 5]
№85.
Избавиться от иррациональности в
знаменателе дроби

1)
 2)
2)
 3)
3)
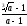 4)
4)

№
86. Найти значение выражения:


1)
 2) 27 3) 21 4)
2) 27 3) 21 4)

№
87. Найти корень уравнения

1)7,6 2) 11 3) -9,5 4) -9
№
88. Решить уравнение
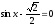
1)
 ;
2)
;
2)
 ;
3)
;
3)
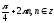 4)
4)
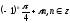
№
89. Найти наибольшее значение функции

1) - 9 2) 10 3) 1 4) 0
№ 90. Указать уравнение, которое не имеет корней
1) 2,7х2 – 1,5х = 0; 2) 2,7х2 + 1,5х = 0; 3) 2,7х2 - 1,5 = 0; 4) 2,7х2 + 1,5 = 0
№ 91 Найти сумму корней квадратного уравнения х2 + 12х + 5 = 0
1) -12 2) нет корней 3) 5 4) 12
№ 92 Маша купила месячный проездной билет на автобус. За месяц она сделала 67 поездок. Сколько рублей она сэкономила, если проездной билет стоит 590 руб., а разовая поездка 12 руб.?
1) 200 2) 214 3) 175 4) 315
№ 93 На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали - значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 8 августа. Ответ дайте в градусах Цельсия.
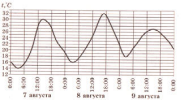
1) 11 2) 22 3) 16 4)9
№ 94 Моторная лодка прошла 10 км по озеру и 4 км против течения реки, затратив на весь путь 1 час. Найти собственную скорость лодки, если скорость течения реки равна 3 км/ч.
1) 15 км/ч 2) 15 км/ч или 2 км/ч 3) 30 км/ч 4) правильного ответа нет
№
95
Упростить
выражение 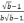
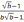
1)

 2)
2) 
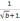 3)
3) 
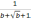 4)
4) 

№
96
Объем
шара –V,
радиус шара – R.
V
= 
 π R3.
Выразить R
через V.
π R3.
Выразить R
через V.
1)

 2)
2) 
 3)
3)

 4)
4) 

№ 97 У фермера 53 куриных и 48 гусиных яиц. Сколько потребуется инкубаторов для вывода птенцов из этих яиц, если в каждый инкубатор можно поместить 19 яиц?
-
6 2) 8 3) 4 4) 10
№
98
Решить
систему неравенств

а) (0; 6) б) (4; 6) в) [0; 2) г) [0; 4]
№
99
Упростить
выражение 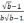
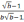
а)

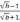 б)
б) 
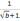 в)
в)
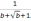
 г)
г) 

№ 100 Среди заданных функций укажите возрастающие:
-
y= - 3x2 2) y= 3-x 3) y= 5x-2 4) y=


а) 2 и 4 б) 1и 4 в) 3 и 4 г) 1; 2 и 4
№ 101 Зная, что f(x)=4х3+х2(х-4) найдите f(2)+f(1)
а) -15,2 б) 25 в) -25 г) 15,2
№102 Исследуйте на ограниченность функцию y= -x2+2x+3
а) ограничена сверху б) ограничена в) ограничена снизу г) не ограничена
№103 Найдите координаты точки
пересечения графика функции y=

 с осью абсцисс
с осью абсцисс
а) (0; 1) б) (-1; 0) в) (-0,5; 0) г) (0; 0,5)
№ 104 Найдите нули функции y = -0,8x+16
а) x=20 б) х=-20 в) х=2 г) х=-2
№ 105 При каких значениях x
выражение 
 не имеет смысла?
не имеет смысла?
а) х=3 и х=-3 б) х=3 в) х=-3и х=-2 г) х=2 и х=1
.№ 106 Разложите на множители квадратный трёхчлен x2+3x-10
а) (х+2)(х+5) б) (х-2)(х+5) в) (х+2)(х-5) г) (х-2)(х+5)
№ 107 Наименьшее целое решение неравенства 2х + 3 > 5:
а) 1 б) 14 в) 2 г) 0,5
№ 108 Вычислите координаты вершины параболы y=2x2-7x+6
а) (0,75; 0,125) б) (-0,75; 0,25) в) (1,75; -0,125) г) (-1,75; 0,125)
№ 109 Назовите степень уравнения 6x4-3x2+1=x
а) четвёртая б) вторая в) первая г) седьмая
№ 110 Решите уравнение y3-9y=0
а) 0; 3 б) -3; 3 в) -3; 0; 3 г) 0
№111 Решите биквадратное уравнение 2x4-3x2+1=0
а) 
 ;
-8 б)
;
-8 б)

 в)
в) 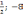
 г)
г) 

№112 Найдите координаты точек пересечения графика функции y=x2-26x+25 с координатными осями
а) (-1; 0), (25; 0) б) (1; 0), (0; 25) в) (25; 0), (1; 0), (0;25) г) (-25; 0), (25; 0)
№113 Найдите область определения
функции 
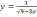
а) (3; +
 )
б) (-
)
б) (-
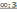 )
в) [3; +
)
в) [3; +
 )
г) (-
)
г) (-
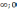 )
)
№114 Среди заданных функций укажите убывающие:
-
y=2x2 2) y=3x-1 3) y=6-2x 4) y=


а) 3 б) 1 и 3 в) 3 и 4 г) 1
№ 115 Среди заданных функций укажите нечетные
-
y=2x2 2) y=
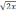
 3) y=5x
4) y=x3
3) y=5x
4) y=x3
а) 1 и 3 б) 2 и 3 в) 3 г) 3 и 4
№ 116 Исследуйте на ограниченность функцию y = x2 - 5x - 2
а) ограничена сверху б) ограничена снизу
в) ограничена и сверху и снизу г) не ограничена
№ 117 Зная, что g(x)
= 
 ,
найдите g(4) - g(-3)
,
найдите g(4) - g(-3)
а) -1,4 б) 1,4 в) -3,8 г) 3,8
№ 118 Найдите координаты точки
пересечения графика функции y=

 с осью ординат
с осью ординат
а) (0; -4) б) (-4; 0) в) (-2; 0) г) (0; 1)
№ 119 Найдите нули функции 

а) x= -90 б) х=90 в) х=9 г) х= -9
№ 120 При каких значениях x
выражение 
 не имеет смысла?
не имеет смысла?
а) x=3 б) х=2; х=-2 в) х=0 г) х=0; х=3
№ 121 Разложите на множители квадратный трёхчлен x2+2x-3
а) (x-1)(x-3) б) (х+1)(х+3) в) (х-1)(х+3) г) (х+1)(х-3)
№ 122 Имеет ли квадратный трёхчлен 9х2-6х+1 корни? (Если да, то сколько?)
а) нет корней б) 2 корня в) 1 корень г) 3 корня
№ 123 Сократите дробь 

а) 
 б)
б) 
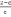 в)
в) 
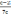 г)
г) 

№ 124 Вычислите координаты вершины параболы y = x2- 4x -5
а) (2; - 9) б) (-2; 9) в) (2; 9) г) (-2; -9)
№ 125 Назовите степень уравнения 7x5 - 5x4 +2 = x
а) десятая б) пятая в) первая г) вторая
№ 126 Решите уравнение y3 - 5y = 0
а) 0; 
 б) -
б) - 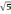
 ;
;

 в) 0 г)
в) 0 г) 

№ 127 Решите биквадратное уравнение x4 - 2x2 - 8=0
а) -2; 2; 0; 4 б) -2; 2 в) 0; 2 г) -2; 0
№ 128 Найдите координаты точек пересечения графика функции y=-x2-3x+10 с координатными осями
а) (0; 10),(2; 0) б) (2; 0),(-5; 0) в) (-5; 0),(0; 10) г) (-5; 0), (2; 0), (0; 10)
№ 129 Какое из нижеуказанных значений является отрицательным числом для функции f(x)=3x2+5x-9
а) f(-4) б) f(-3) в) f(-5) г) f(0)
№ 130 Найдите наименьшее значение функции у = 3x2 + 6x - 9
а) 12 б) -12 в) -15 г) -9
№ 131 Найдите все решения неравенства (x+3)(5+2x) ≤ 0
а) [-3; -2,5] б) (
 в) (-3; -2,5) г) (
в) (-3; -2,5) г) (
 )
)

№ 132 Укажите количество целых решений неравенства 2x2 + 5x – 3 ≤ 0
а) 3 б) 2 в) 4 г) 0
№ 133 Преобразуйте выражение (с – 3)2 – (с - 4)*с в многочлен
а) 10с – 9 б) -2с + 9 в) 2с + 9 с) 10с + 9
№ 134 Спортсмен преодолел дистанцию в х км за t мин. Определить, с какой средней скоростью (в км/ч) он бежал.
а)
 б)
б)
 в)
в)
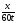 c)
c)

№ 135 Вычислить: -10*(2,25)1/2 – (-2,25)0
а) -14 б) -16 в) – 15 4) 1,25
№ 136 Запишите в порядке возрастания числа 1/7; 0,111; 0,2
а) 1/7; 0,111; 0,2 б) 0,2; 1/7; 0,111 в) 1/7; 0,2; 0,111 г) 0,111; 1/7; 0,2
№ 137 Найти значение выражения cos 340cos 260 – sin 340sin 260
а) 1 б) 14 в) 0,5 г) другой ответ
№ 138 Найти число, 70% которого равны 25% от 28.
а) 1) 78,4; б) 10 в) 4,9; г) 160
№ 139 Какая из предложенных пар чисел является решением уравнения
2х(у – 2ху) = 1 – у2 ?
а) (1; 1) б)(2; 2) в) (0;0) г) (0; 1)
№ 140 Какое из данных выражений положительно, если a = 1400?
