13. 3. Теорема 1.

Всякое сравнение вида ах  b (mod m) равносильно некоторому неопределённому уравнению 1-й степени с двумя неизвестными и целыми коэффициентами вида nx + ky = t ( при некотором условии верно и обратное утверждение).

В самом деле:

1) Дано сравнение ах  b (mod m)  (ах – b) m  ах – b = mу (уZ)  ах – mу = b – уравнение 1-й степени.

2) Дано уравнение ах + bу = с, (где а,bZ и (а; b) = 1)  ах – с = – bу  (ах – с) b  ах  с (mod b) – линейное сравнение.

13. 4. Определение 2.

Тождественным сравнением называется сравнение, которое истинно при любых (целых) значениях неизвестной.

Например: рассмотрим сравнение 6х  9 (mod 3). При любом х₀ = с  Z имеем: (6с – 9) 3  по лемме 6с  9 (mod 3) – "И", то есть произвольное число с удовлетворяет данному сравнению, а значит, это сравнение – тождественное.

13. 5. Теорема 2.

Если в сравнении ах  b (mod m) коэффициенты а и b кратны модулю , – то такое сравнение – тождественное.

Например, в сравнении 6х  9 (mod 3) 6 3 и 9 3. По теореме 2 оно – тождественное.

13. 6. Теорема 3.

Если сравнение ах  b (mod р) по простому модулю р имеет 2 класса решений, – то оно – тождественное.

§ 14. Системы линейных сравнений с одной неизвестной основные сведения из теории

14. 1. Определение 1.

Системой линейных сравнений с одной неизвестной называется система вида
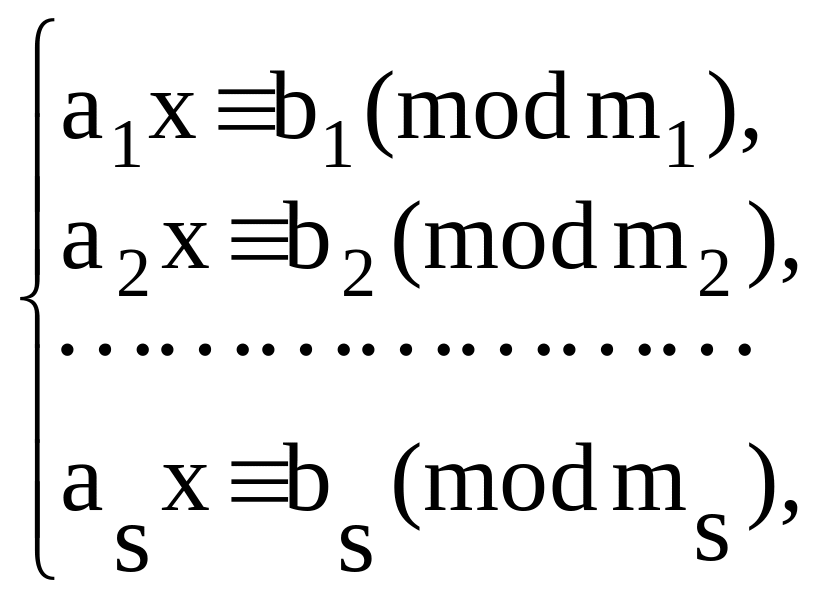
	где аi , bi., x Z, тi  N. тi >1, (*) ai не тi (i = 1, 2, ... , s).

14. 2. Определение 2.

Решением системы (*) называется класс вычетов, удовлетворяющий каждому сравнению этой системы.

Если система (*) имеет хотя бы один класс решений, то она называется

совместной (и в противном случае – несовместной).

14. 3. Следствие 1.

Если хотя бы одно из сравнений системы (*) не имеет решений, то и вся система (*) не имеет решений (то есть несовместна).

14. 4. Теорема 1.

Рассмотрим систему (**) – частный случай системы (*):
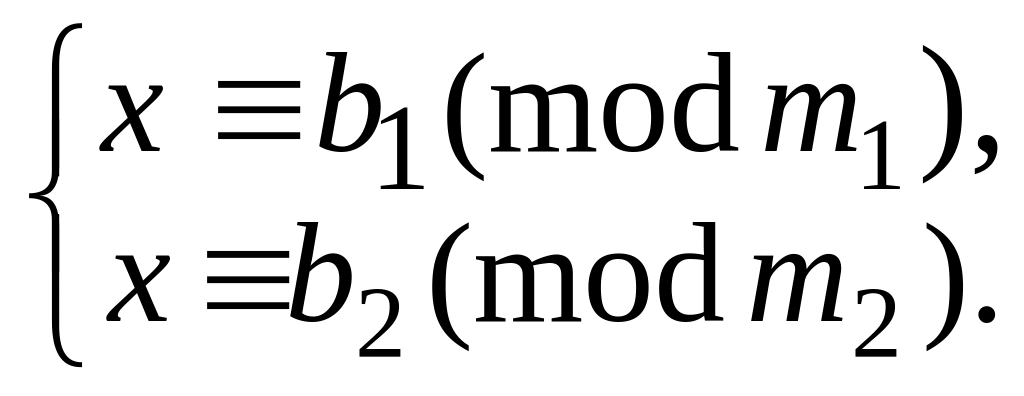(**)	Пусть НОД (т1; т2) = (т1; т2) = d, НОК (т1; т2) = [т1; т2] = m.
Тогда: 1) если (b2 – b1) не d, то система (**) не имеет решений; 2) если (b2 – b1) d, то система (**) имеет 1 класс решений по модулю [т1; т2] = m.

14. 5. Следствие 2.

Если (т₁; т₂) = d = 1, – то т = т₁  т₂ и система (**) совместна и имеет один класс решений по модулю т = т₁  т₂ .

Заметим, что теорема 1 может быть обобщена на случай, когда система (**) содер- жит произвольное (конечное) число сравнений вида x  b_j (mod m _j).

В частности, если т₁, т₂ , … , т_s – взаимно простые числа, то система (**) всегда совместна и имеет 1 класс решений по модулю т₁  т₂  …  т_s .

14. 6. Вернёмся к рассмотрению системы сравнений (*) вида a_i x  b_j (mod m _j).

1) Обозначим (a_i ; m_i) = d_i (i = 1, ... , s). Если хотя бы при одном значении i b_i не d_i, то i-е сравнение системы не имеет решений, а, значит, и вся система (*) несовместна.

2) Если же b_i d_i для всех i, то каждое сравнение системы (*) можно решить относительно x и заменить систему (*) равносильной системой (***) :

(***)

Эта система либо несовместна, либо имеет 1 класс решений по модулю [m1: d1, ... , ms : ds] .

14. 7. Линейные сравнения по составному модулю вида ax  b (mod p₁  р₂ ).

Так как (ах – b) (р₁  р₂), то 
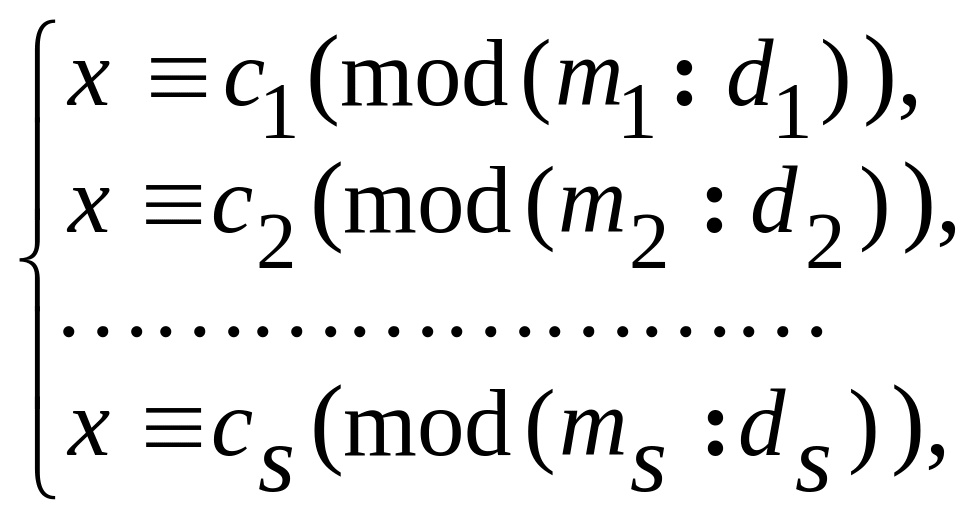