Из третьего уравнения найдем

После этого из второго уравнения определим

Непрерывно распределенная нагрузка из параллельных сил.
На практике, кроме сил, действие которых сосредоточено в одной точке, часто встречаются силовые нагрузки, действие которых распределено вдоль линии, по поверхности или по объему тела. Такие силовые воздействия называются непрерывно распределенными нагрузками. Их действие на тело характеризуется интенсивностью q, которая в зависимости от вида нагрузки в системе СИ выражается в н/м, 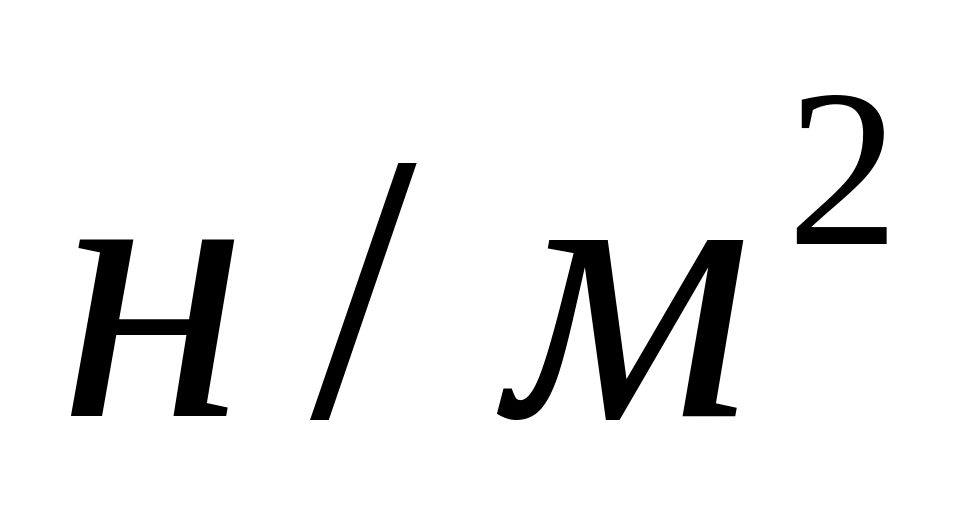или 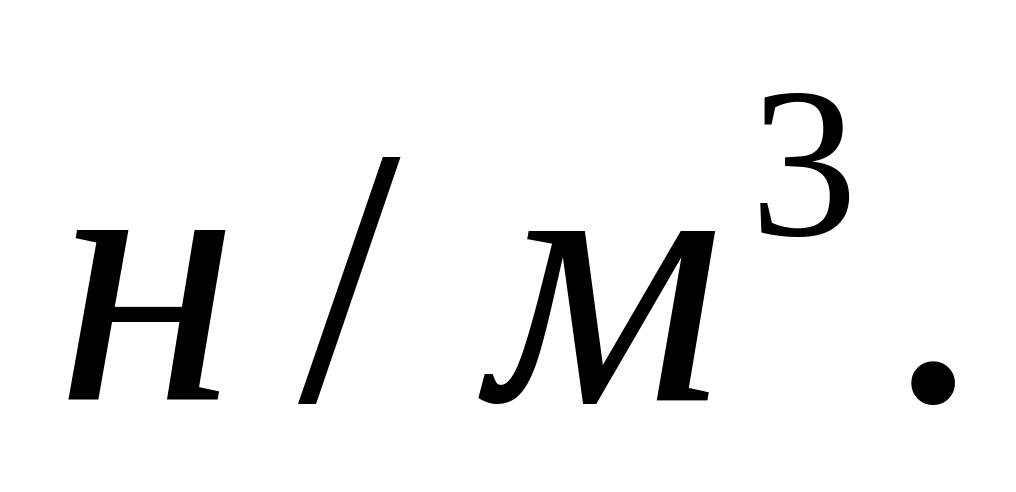Далее ограничимся рассмотрением простейшего вида непрерывно распределенной нагрузки: нагрузки из параллельных сил, непрерывно распределенной вдоль отрезка прямой линии. Пусть нагрузка распределена вдоль отрезка АВ. Направим вдоль этого отрезка ось x и построим график интенсивности действующей нагрузки q(x) (см. рис. 74). Стрелками под графиком покажем направление сил нагрузки. Получившуюся геометрическую фигуру называют эпюрой непрерывно распределенной нагрузки.

Рис. 74.

Докажем теперь одну из важных теорем статики.

Теорема Вариньона.

Если система сил имеет равнодействующую, то векторный момент равнодействующей силы относительно любого центра равен геометрической сумме векторных моментов всех сил системы, вычисленных относительно того же центра.

Доказательство.

Пусть система сил имеет равнодействующую силу . Это можно выразить соотношением эквивалентности

Добавим к системе сил силу равную по величине и направленную в противоположную сторону вдоль линии действия Тогда соотношение эквивалентности для полученной системы сил перепишется в виде

Это означает, что система сил является уравновешенной. Для такой системы сил справедливо уравнение равновесия (117):

Учитывая, что отсюда получим

(119)

Это равенство выражает утверждение теоремы.

Если векторное равенство (119) записать в проекциях на выбранные оси координат, то получим, что аналогичная теорема справедлива не только для векторных моментов сил, но и для моментов сил относительно осей, а также для алгебраических моментов сил в случае рассмотрения плоской системы сил.

Покажем теперь, как рассматриваемую непрерывно распределенную нагрузку заменить равнодействующей силой. Из школьного курса физики известно, что две одинаково направленные параллельные силы имеют равнодействующую, равную по величине сумме этих сил и направленную в ту же сторону.

Рис. 75.

Разобьем отрезок длиной l , на котором распределена нагрузка, на элементарные участки длиной dx. Действие нагрузки на каждом из таких участков может быть выражено силой (см. рис. 75). Суммируя такие силы и переходя к пределу при для величины равнодействующей силы получим

(120)

Для нахождения точки приложения равнодействующей силы применим теорему Вариньона для алгебраических моментов относительно точки О. После предельного перехода при получим (см. рис. 75)