Осевые моменты инерции простейших однородных тел.
Прямолинейный стержень.
Вычислим момент инерции прямолинейного стержня длиной АВ=l относительно оси , проведенной перпендикулярно стержню через его центр масс С (см. рис. 59).
Рис. 59.
Обозначим массу стержня М. Направим
вдоль стержня ось x
с началом в точке С. Выберем на стержне
элементарный участок длиной dx
на расстоянии x
от начала координат. Обозначим массу
этого элементарного участка dm.
Очевидно, что
- линейная плотность стержня (масса
единицы его длины). Тогда момент инерции
выделенного элемента равен
а для момента инерции стержня АВ относительно оси получим
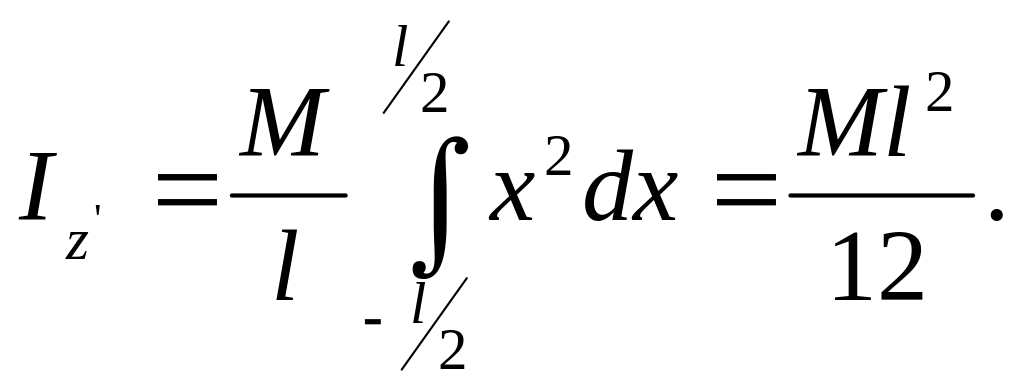(63)
Вычислим с помощью теоремы Штейнера момент инерции стержня относительно оси z , проходящей через конец стержня:
(64)
Круговое кольцо.
Вычислим момент инерции кругового
кольца массой М и радиуса R
относительно оси
проведенной перпендикулярно плоскости
кольца через его центр масс С (см. рис.
60). Учитывая, что расстояние от каждой
точки кольца до рассматриваемой оси
равно R, получим:
(65)
Рис. 60.
Круговой диск.
Рассмотрим круговой диск массой М
с радиусом R .
Вычислим его момент инерции относительно
оси
(см. рис. 61).
В качестве элемента поверхности диска
выберем тонкое кольцо радиуса r
и толщиной dr . Массу
этого элемента dm можно
выразить через его площадь
и поверхностную плотность
:
Рис. 61.
Момент инерции выбранного элемента относительно рассматриваемой оси в соответствии с (65) будет
Тогда для искомого момента инерции диска получим
(66)
Глава 4, Общие теоремы динамики.
Теорема о движении центра масс.
Выведем формулу, выражающую данную теорему. Запишем уравнения движения точек механической системы в векторной форме (см. (55))
Почленно сложим записанные равенства, получим
(67)
Продифференцируем дважды по времени формулу (58) для радиуса-вектора центра масс, получим:
Учитывая также, что в соответствии с
теоремой об основных свойствах внутренних
сил
из (67) получим:
(68)
Формула (68) выражает теорему о движении центра масс, которая обычно формулируется в виде:
Центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы.
Сделаем несколько замечаний, поясняющих физический смысл доказанной теоремы и ее практическое использование.
Замечания.
1. Равенство (68) является векторным и при решении задач его следует записывать в проекциях на выбранные оси координат. Например, в проекциях на оси декартовой системы координат оно примет вид:
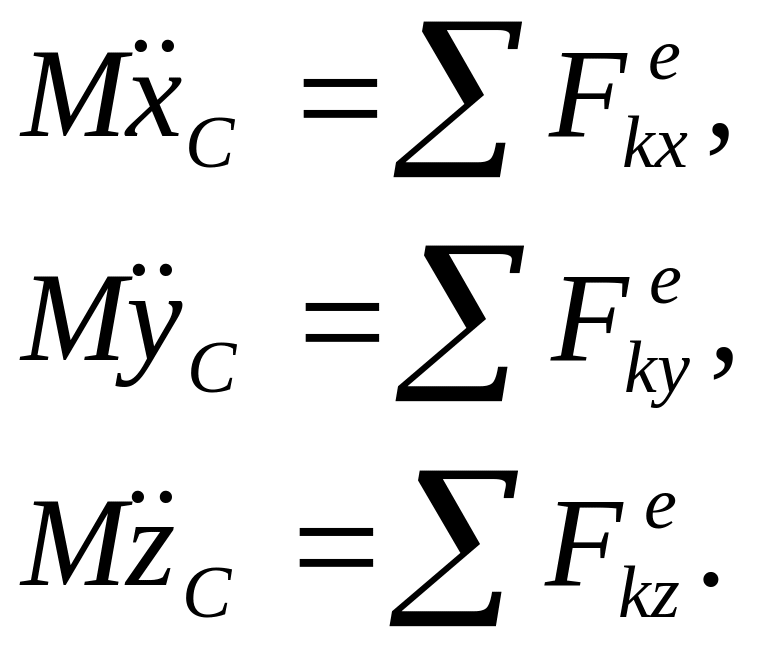(68’)
2. С помощью этой теоремы можно детально изучать движение только одной точки механической системы – ее центра масс. Так как при поступательном движении твердого тела все его точки, в том числе и центр масс, движутся одинаково, то с помощью этой теоремы можно изучать поступательное движение твердого тела. Поэтому уравнения (68’) называют еще дифференциальными уравнениями поступательного движения тела.
3. Внутренние силы механической системы не могут изменить движения ее центра масс.
Из теоремы о движении центра масс можно получить следствия, являющиеся частными случаями этой теоремы.
Следствие 1. Если проекция, например
на ось Ох, главного вектора внешних
сил, действующих на систему, равна нулю,
т. е.
то из (68’) следует, что проекция скорости
центра масс на эту ось является постоянной
величиной:
Следствие 2. Если дополнительно к
в начальный момент
то при движении механической системы
координата
остается неизменной:
Пример 8.
Механическая система состоит из бруска
А массой
,
опирающегося на гладкую горизонтальную
плоскость, и шарнирно соединенного с
ним в точке О однородного стержня ОВ
длиной l=ОВ=1м и
массой
Точка О является центром масс бруска
А. В начальный момент система находилась
в состоянии покоя и стержень ОВ занимал
горизонтальное положение. Требуется
определить перемещение бруска А к
моменту времени, когда стержень займет
вертикальное положение (см. рис. 62).
Рис. 62.
Решение.
Внешними силами, действующими на тела
системы, будут силы тяжести
и нормальная реакция гладкой опорной
плоскости
Направим ось x вдоль
опорной плоскости, начало координат
совместим с начальным положением точки
О. Тогда
Учитывая, что в начальный момент времени
система находилась в покое, из второго
следствия получим
Выразим координату
для начального и конечного положений
системы
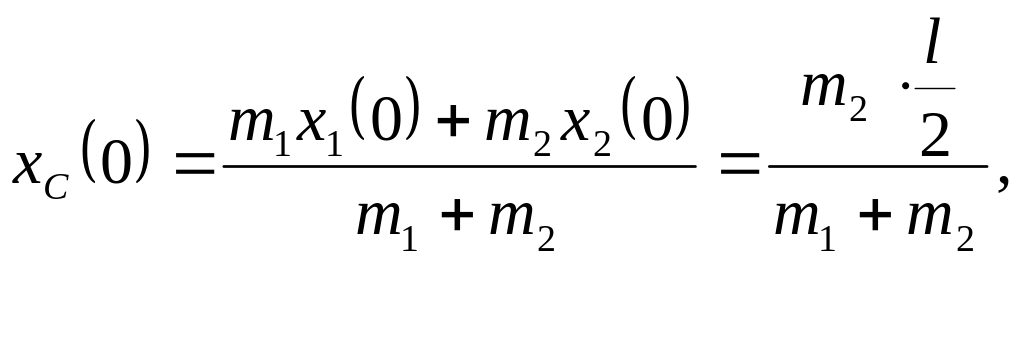
Приравнивая полученные значения, найдем искомое перемещение бруска:
