
- •Тема 1. Предмет, метод и задачи статистики
- •4. Основные категории и понятия статистики:
- •Тема 2. Организация государственной статистики в рф и международной статистики
- •Тема 3. Статистическое наблюдение
- •Тема 4. Сводка и группировка
- •1) Ряд распределения рабочих по стажу
- •2) Ряд распределения рабочих по стажу
- •Тема 5. Средние величины
- •3.Структурные средние величины.
- •Тема 6.Показатели вариации
- •2. Абсолютные и средние показатели вариации и способы их расчета
- •3. Показатели относительного рассеивания
- •3. Коэффициент вариации:
- •Тема 7. Абсолютные и относительные величины
- •Виды относительных величин.
- •Ов выполнения договорных обязательств.
- •Ов выполнения плана (процент выполнения плана)
- •Ов планового задания (плановый темп роста)
- •Ов интенсивности
- •Тема 8. Ряды динамики
- •3. Средние показатели ряда:
- •З адача
- •Тема 9. Индексный метод в статистике
- •2. Общие и индивидуальные индексы
- •3. Средневзвешенные индексы
- •4. Индексный метод анализа динамики среднего уровня
3. Средние показатели ряда:
Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
В интервальных рядах динамики средний уровень определяется делением суммы уровней на их число:
![]() .
.
В моментном ряду динамики с равностоящими датами времени средний уровень определяется по формуле средней хронологической:
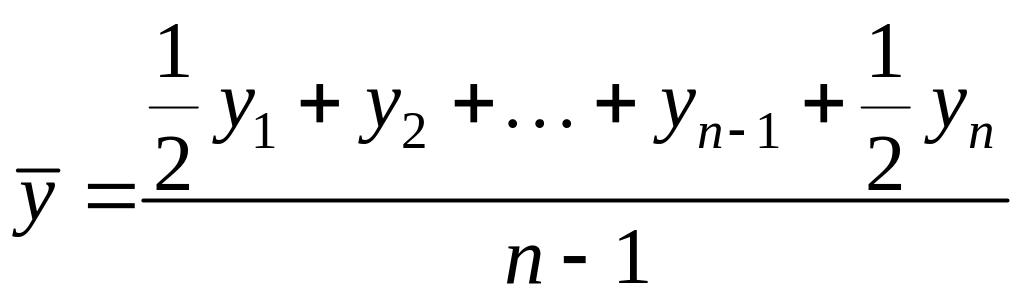
У нас в примере ряд интервальный, следовательно:
![]()
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:
![]() .
.
![]()
Средний темп роста – обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста применяется формула средней геометрической из показателей коэффициентов роста:
![]() ,
где
– число темпов роста, или
,
где
– число темпов роста, или
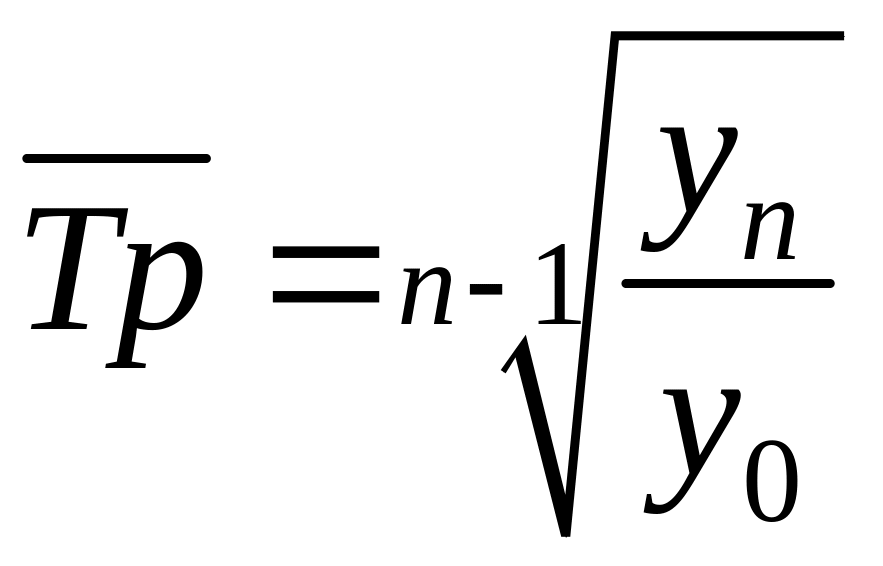 ,
где
,
где
![]() – число уровней ряда, уменьшенное на
1.
– число уровней ряда, уменьшенное на
1.
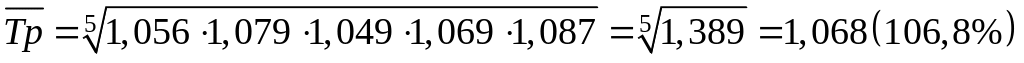 ,
,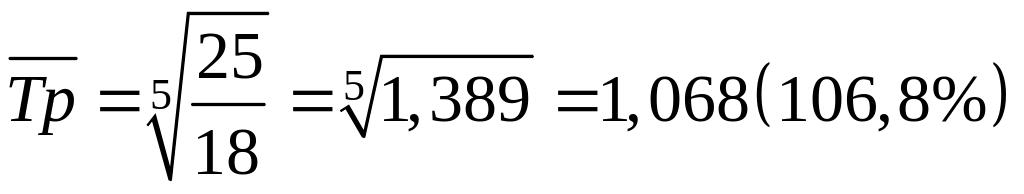 .
.
Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста. При наличии данных о средних темпах роста для получения средних темпов прироста используется зависимость:
![]() (при
выражении среднего темпа роста в
коэффициентах),
(при
выражении среднего темпа роста в
коэффициентах),
![]() (при
выражении среднего темпа роста в
процентах).
(при
выражении среднего темпа роста в
процентах).
![]() .
.
Среднее абсолютное содержание 1% прироста вычисляется делением суммы значений абсолютного содержания 1% прироста на их число:
![]() .
.
![]()
Графически ряды динамики могут быть представлены в виде линейного графика, диаграммы, структурной диаграммы, картограммы, картосхемы.
З адача
Численность рабочих предприятия по месяцам года характеризуются следующими данными (чел.):
на 01.01 2150
на 01.02 2130
на 01.03 2156
на 01.04 2160
на 01.05 2154
на 01.06 2168
на 01.07 2180
на 01.08 2205
Известно, что среднесписочная численность рабочих за III квартал составила 2172 чел., за IV квартал – 2181 чел.
Определите среднесписочную численность рабочих за I-е полугодие, за II-е полугодие и за год в целом.
Решение: Т.к. приведен моментный ряд, расчет производится по средней хронологической:
За I-е полугодие:
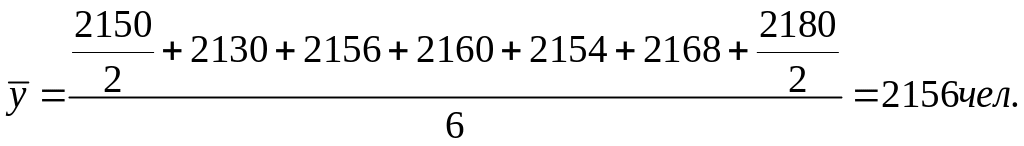
По кварталам:
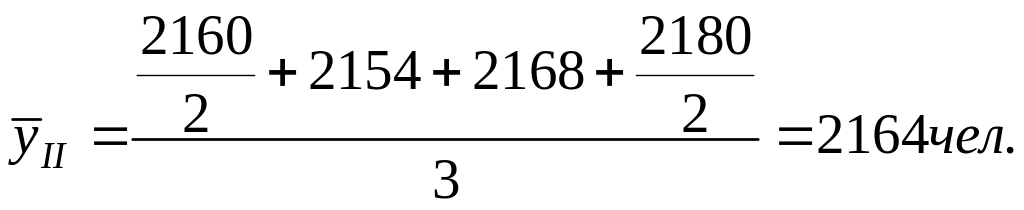
За
II-е
полугодие:
![]()
За
год: ![]()
Задача
Ежегодный прирост продукции промышленного предприятия за 2010-2014 г.г. характеризуется следующими данными (в % к предыдущему году):
2010 |
2011 |
2012 |
2013 |
2014 |
3 |
6 |
5 |
7 |
8 |
Исчислите базисные темпы роста (2010 = 100) пр-ва продукции за эти годы и среднегодовой темп роста.
Решение:
Т.к. , то темпы прироста составят соответственно: (см. таблицу). Затем воспользуемся формулой, что произведение цепных темпов равно базисную, предварительно сделав базисным 2010 год.
2010 |
2011 |
2012 |
2013 |
2014 |
|
3 |
6 |
5 |
7 |
8 |
прирост цепной |
103 |
106 |
105 |
107 |
108 |
рост цепной |
100,0 |
106,0 |
111,3 |
119,1 |
128,6 |
рост базисный |
![]() .
.
