2.2 Методические указания

2.2.1 Преобразование Лапласа и его основные свойства

Наиболее распространенным методом описания и анализа линейных непрерывных систем является метод операционного исчисления, в основе которого лежит прямое интегральное преобразование Лапласа.

Прямым преобразованием Лапласа называют соотношение

, (2.1)

устанавливающее соответствие между функцией действительной переменной x(t) и функцией комплексной переменной X(s) ( ).

Функцию x(t) называют оригиналом, а функцию X(s) изображением или изображением функции x(t) по Лапласу.

Преобразование выполнимо лишь для функций, которые обладают следующими свойствами:

1. функция x(t) определена и кусочно дифференцируема на интервале ;

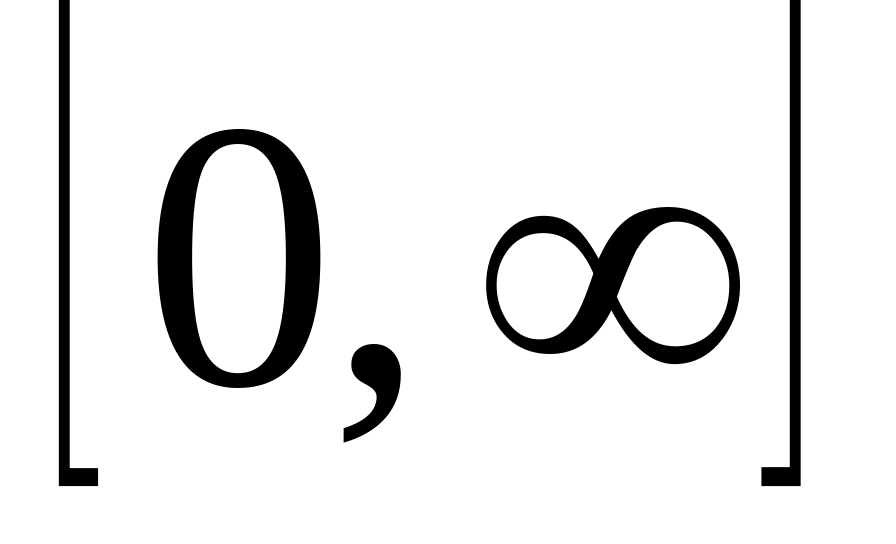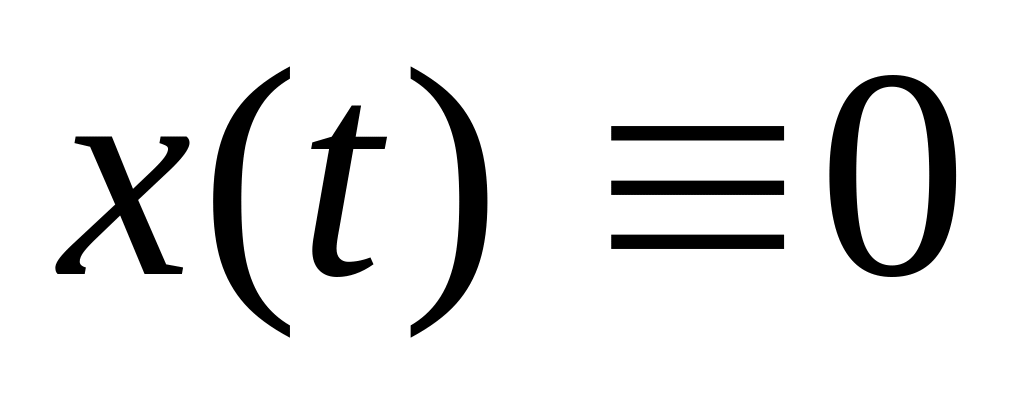2. при t <0;

3. Существуют такие положительные числа с и М, что при 0≤ t<∞.

Соотношение

, (2.2)

определяющее по известному изображению переменной ее оригинал называется обратным преобразованием Лапласа.

Условно прямое преобразование Лапласа записывают в виде ; обратное преобразование Лапласа - , L – оператор Лапласа,

L^-1 – обратный оператор Лапласа.

Для преобразования линейных дифференциальных уравнений используются следующие свойства преобразования Лапласа:

1. Свойство линейности. Для любых постоянных α и β

. (2.3)

2. Дифференцирование оригинала

,

где , - начальные условия. При нулевых начальных условиях

. (2.4)

Для n-ой производной

,

.

При нулевых начальных условиях

(2.5)

Таким образом, при нулевых начальных условиях дифференцирование оригинала соответствует умножению изображения на s.

3. Интегрирование оригинала

. (2.6)

2.2.2 Передаточная функция в изображениях Лапласа

Передаточной функцией системы (звена) в изображениях Лапласа W(s) называют отношение изображения выходной переменной к изображению входной переменной при нулевых начальных условиях.

Если - изображение по Лапласу выходной переменной, - изображение по Лапласу входной переменной, передаточная функция определяется выражением

(2.7)

В соответствии с определением для получения передаточной функции необходимо записать дифференциальное уравнение в изображениях Лапласа при нулевых начальных условиях, пользуясь свойствами преобразования Лапласа (2.3-2.6), и из него выразить отношение Y(s)/U(s). Пример определения передаточной функции приведен в приложении А.

3 Задание 2

3.1 Условие задачи

Построить амплитудно-фазовую частотную характеристику и логарифмические частотные характеристики динамического элемента по заданной передаточной функции при изменении частоты от 0 до + ∞. Вид динамического звена определить по предпоследней цифре номера зачетной книжки согласно таблице 3.1.

Таблица 3.1- Варианты задания

№ варианта	Вид динамического звена
1	2
0
1
2
3
4
5
6
7

Продолжение таблицы 3.1

1	2
8
9

Параметры звена определить по последней цифре шифра согласно таблице 3.2.

Таблица 3.2- Параметры звена

Вариант	0	1	2	3	4	5	6	7	8	9
	20	5	100	1	8	40	10	15	2	200
	0,1	0,03	0,02	0,05	0,2	0,15	0,04	0,5	1	0,4
	0,15	0,4	0,8	1	0,5	0,05	0,03	0,3	0,25	0,08
	0,5	0,1	1,5	2	1,5	0,1	0,1	0,8	0,05	0,3
Т3	0,35	0,25	1	0,5	0,8	0,4	0,6	0,5	0,1	0,2