Тема 1. Элементы линейной алгебры Лекция № 1 Тема: Общие понятия системы линейных уравнений.

Тема: Матрицы и определители

1. Понятие матрицы. Виды Матриц.

2. Действия над матрицами.

3. Виды определителей и правила их вычисления.

4. Минор, алгебраическое дополнение.

1. Понятие матрицы. Виды Матриц.

Определение. Матрицей размера m n называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

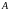= или = , =1,2,…, , 1,2,…, .

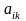– элемент матрицы, стоящий на пересечении -й строки и -го столбца.

Определение. Если , то матрица называется квадратной n-го порядка, в противном случае – прямоугольной.

Элементы , = 1, 2, …, n квадратной матрицы А образуют ее главную диагональ.

Матрица размера 1хn называется матрицей-строкой, а матрица размера – матрицей-столбцом.

Определение. Две матрицы называются равными, если они имеют одинаковый размер и равны их элементы, стоящие на одинаковых местах.

Определение. Квадратная матрица называется диагональной, если равны нулю все ее элементы, расположенные вне главной диагонали, то есть

На главной диагонали могут быть любые числа. Если все они равны 1, то диагональная матрица называется единичной и обозначается буквой .

Определение. Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.

2. Действия над матрицами

1) Сложение и вычитание матриц

Складывать и вычитать можно матрицы одного размера в результате получается матрица того же размера.

Определение. Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

сij = aij + bij

Определение. Вычитание матриц (разность матриц) A - B есть операция вычисления матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

с_ij = a_ij - b_ij

Примеры задач на сложение и вычитание матриц

2) Умножение матриц

Определение. Результатом умножения матриц A_m×n и B_n×k будет матрица C_m×k такая, что элемент матрицы C, стоящий в i-той строке и j-том столбце (c_ij), равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:

c_ij = a_i1 · b_1j + a_i2 · b_2j + ... + a_in · b_nj

Замечание. Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Свойства умножения матриц

• (A · B) · C = A · (B · C) - произведение матриц ассоциативно;

• (z · A) · B = z · (A · B), где z - число;

• A · (B + C) = A · B + A · C - произведение матриц дистрибутивно;

• E_n · A_nm = A_nm · E_m = A_nm - умножение на единичную матрицу;

• A · B ≠ B · A - в общем случае произведение матриц не коммутативно.

• Произведением двух матриц есть матрица, у которой столько строк, сколько их у левого сомножителя, и столько столбцов, сколько их у правого сомножителя.