Имеющей распределение Райса (обобщенное распределение Релея)
С
ростом значения параметра
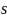эта функция сходится к гауссовской
плотности вероятности с математическим
ожиданием
и дисперсией
.
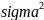При
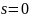распределение переходит в распределение
Релея.
Пример:
pd = makedist(‘rician’, ‘s’, 4, ‘ ’, 2);
y=random(pd, 10000, 1); % Выборка объема n=10000;
x=0:0.01:15;
;
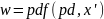plot(x,w)
2.5 . Формирование вещественного массива выборочных значений случайной величины, имеющей распределение Релея
Синтаксис:
pd = makedist(‘Rayleigh’, ‘b’, 2);
y=random(pd, n, 1);
Описание:
Функция
MATLAB pd
= makedist(‘Rayleigh’,
‘
’,
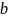2) создает скрипт-файл распределения
Релея с параметром масштаба
.
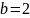Функция MATLAB y= random(pd, n, 1) генерирует массив y размера , элементами которого являются выборочные значения случайной величины, имеющей плотность вероятности pd.
Аналитическое выражение для соответствующей плотности вероятности имеет вид:
,
.
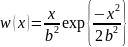Рис.6. Плотность вероятности распределения Релея
График этой плотности, представлен на рис.6 для .
График построен с помощью функции MATLAB , где – массив значений аргумента плотности вероятности, для которого вычисляются значения плотности .
Пример:
pd = makedist(‘Rayleigh’, ‘ ’, 2);
y=random(pd, 10000, 1); % Выборка объема n=10000;
x=0:0.01:15;
;
plot(x,w)
2.6 . Формирование вещественного массива выборочных значений случайной величины, имеющей логарифмически нормальное распределение
Синтаксис:
pd = makedist(‘Lognormal’, ‘mu’, 2, ‘ , 1); w=
y=random(pd, n, 1);
Функция y=random(pd, n,1) формирует выборку y размера , элементами которой являются выборочные значениями случайной величины, имеющей логарифмически нормальное (логнормальное) распределение.
Рис. 7. Плотность вероятности логарифмически нормального распределения
Функция
MATLAB pd
= makedist(‘Lognormal’,
‘mu’, 2, ‘
’,
1) создает скрипт-файл логарифмически
нормального распределения с параметром
нецентральности mu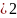
и масштаба
.
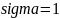Аналитическое выражение для соответствующей плотности вероятности имеет вид:
,
.
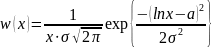График
этой плотности для mu
и
приведен на рис.7. График построен с
помощью функции MATLAB w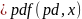
,
где
– массив значений аргумента плотности
вероятности, для которого вычисляются
значения w плотности
.
Пример:
pd = makedist(‘Lognormal’,’mu’,2, ‘ ’, 2);
y=random(pd, 10000, 1); % Выборка объема n=10000;
x=0:0.01:70;
;
plot(x,w)
2.7 . Формирование вещественного массива выборочных значений случайной величины, имеющей полигауссовское распределение
Синтаксис:
;
;
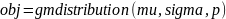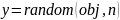Описание:
mu
– матрица размера
,
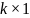определяющая математические ожидания
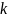гауссовских случайных величин, являющихся
компонентами смеси;
– определяет
ковариации каждой компоненты смеси;
размер матрицы
в данной работе равен
;
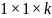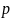– вектор размера
,
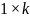определяющий вероятности появления
выборочных значений гауссовских
компонент.
Функция формирует матрицу размера выборочных значений случайной величины с плотностью вероятности obj.
Полигауссовская плотность вероятности может быть задана аналитически следующим выражением :
,
.
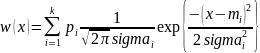На рис.8 представлен график полигауссовской плотности для следующих численных значений параметров:
.
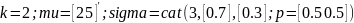Рис.8. Плотность полигауссовского распределения
График
построен с помощью функции MATLAB
.
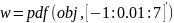Здесь
– массив значений плотности вероятности
obj для значений
[-1:0.01:7] аргумента
.
Пример:
obj=
gmdistribution([2 5]’,
;
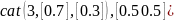y=random(obj, 10000); % Выборка объема n=10000;
x=0:0.01:7;
;
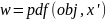plot(x,w)