3.6 . Вопросы для самопроверки

1. Поясните смысл термина «схема испытаний Бернулли».

2. Что такое «повторная выборка», «выборочное значение случайной величины»?

3. Что такое эмпирическая функция распределения? Для чего она нужна?

4. Дайте определение выборочного среднего и выборочной дисперсии. Какие свойства случайной величины характеризуют эти понятия?

5. Приведите пример события, связанного со случайной величиной. Что такое относительная частота события? Как она определяется?

6. Дайте определение начального момента второго порядка. Как он вычисляется?

7. Каким образом по гистограмме, построенной по выборочным значениям случайной величины в схеме испытаний Бернулли, можно получить представление о плотности вероятности этой случайной величины.

8. Приведите пример реальной физической величины, которую необходимо рассматривать как случайную величину.

3.7. Приложение 1. Датчики псевдослучайных чисел

1. Общая информация о датчиках

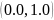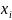Равномерно распределенные псевдослучайные числа обычно генерируются детерминированным рекуррентным алгоритмом со значениями из интервала . В качестве значения очередного элемента выборки используется дробная часть значения некоторого специально выбранного сложного арифметического выражения, являющегося функцией от значения предшествующего элемента выборки .

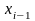Обычно перед использованием датчика случайных чисел задается начальное значение 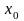. Задание различных позволяет получать различные последовательности или различные выборки. В результате таких вычислений получают “квазислучайные” (псевдослучайные) числа. При увеличении объема выборки числа могут повторяться. Количество неповторяющихся чисел в выборке является параметром датчика, называемым периодом; значение периода является важным параметром датчика и может принимать значения от нескольких сотен тысяч до нескольких миллионов.

Квазислучайные числа с различными функциями распределения, отличными от равномерного, получают обычно из равномерно распределенных квазислучайных чисел с помощью соответствующих функциональных преобразований.

2 . Описание встроенных датчиков псевдослучайных чисел системы MATLAB

Используемая в лабораторном практикуме система MATLAB имеет встроенные датчики псевдослучайных чисел, которые можно использовать при имитационном моделировании радиотехнических систем и устройств в качестве источников случайных сигналов. При каждом обращении к такому датчику можно получить одно или заданное число выборочных значений случайной величины, обладающей известными вероятностными характеристиками. Обычно датчики позволяют получать выборки достаточно большого объема с независимыми элементами и известной функцией распределения. В данном разделе приводятся необходимые сведения о датчиках квазислучайных чисел, которые должны быть использованы при выполнении данной лабораторной работы.

2.1 . Формирование вещественного массива выборочных значений случайной величины, имеющей равномерное распределение на открытом интервале (0.0, 1.0)

Синтаксис:

y=rand(n,1)

Описание:

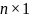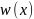Функция MATLAB y=rand(n,1) формирует матрицу размера , элементами которой являются выборочные значения случайной величины, имеющей равномерное распределение на интервале (0,1). На рис.2 изображен график плотности вероятности случайной величины с равномерным распределением, построенный с помощью функции MATLAB w=unifpdf(x, 0,1), где w – массив значений функции , x – массив значений аргумента этой функции.

Рис. 2. Плотность вероятности случайной величины