3.4. Метод построения гистограммы

Определение: ступенчатая фигура, составленная из прямоугольников, основаниями которых служат подинтервалы длины 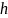, а высоты равны , где 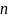– объем выборки 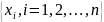, 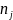- число элементов выборки, попавших в подинтервал , называется гистограммой выборки; отношение 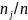называется относительной частотой попадания элементов выборки в подинтервал , .

Практически гистограмма может быть построена следующим образом:

1. определяется размах выборки

,

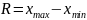где , , ;

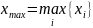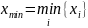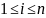2. число 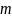подинтервалов, на которые следует разбить размах выборки 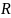(т.е. интервал ), выбирается таким, чтобы каждый подинтервал содержал достаточно большое число выборочных значений;

3. определяется длина подинтервала по формуле

;

4. границы подинтервала с номером 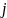на числовой оси находятся по формулам:

, ;

интервал числовой оси делится на подинтервалы длины ;

Рис.1. Гистограмма выборки случайной величины с гауссовским распределением

5. подсчитывается число элементов выборки , относительная частота события и вычисляется значение гистограммы на данном подинтервале;

6. на каждом подинтервале длины h строится прямоугольник с высотой .

На рис. 1 изображена гистограмма, представляющая собой набор 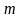прямоугольников, ширина каждого из которых равна 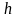, а высота - .

В MATLAB имеется специальная функция hist, обеспечивающая возможность автоматизации процедуры построения гистограммы.

3.5. Метод построения эмпирической функции распределения

Эмпирической функцией распределения называется функция 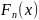, равная при каждом вещественном относительной частоте события , вычисленной по рассматриваемой выборке :

Функция распределения случайной величины 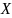, для которой получена выборка, называется теоретической; в соответствии с определением 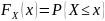, т.е. равна вероятности события, указанного в фигурных скобках. Эмпирическая функция распределения 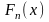есть относительная частота того же случайного события , связанного со случайной величиной , вычисленная по выборке . Известно (закон больших чисел в форме Бернулли), что в схеме испытаний Бернулли относительная частота события стремится по вероятности к вероятности этого события при неограниченном увеличении объема выборки , т.е.

, ,

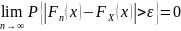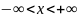для любого сколь угодно малого положительного числа .

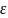Отсюда следует возможность и целесообразность приближенного представления функции 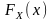функцией 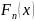. Действительно, обладает всеми свойствами функции распределения вероятностей:

1. ;

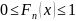2. – неубывающая функция от ;

3. при ;

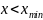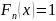4. при .

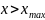Можно также показать, что математическое ожидание и дисперсия эмпирической функции распределения определяются выражениями:

.

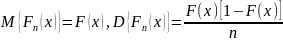Таким образом, эмпирическая функция распределения может быть использована как оценка неизвестной функции распределения случайной величины ; эта оценка строится по повторной выборке значений случайной величины.

Эмпирический начальный момент k-го порядка случайной величины:

,

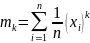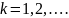
Эмпирический центральный момент k-го порядка случайной величины:

,
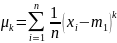