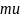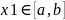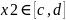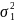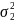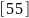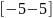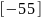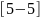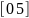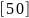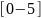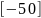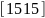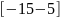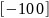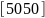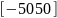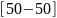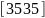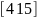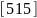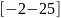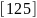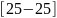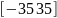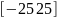4.9. Вопросы для самопроверки

1. Поясните смысл термина «схема испытаний Бернулли».

2. Что такое «повторная выборка», «выборочное значение случайной величины»?

3. Что такое эмпирическая функция распределения? Для чего она нужна?

4. Дайте определение выборочного среднего и выборочной дисперсии. Что характеризуют эти понятия?

5. Приведите пример события, связанного со случайным вектором. Что такое относительная частота события? Как она определяется?

6. Дайте определение начального смешанного момента второго порядка. Как он вычисляется?

7. Каким образом по гистограмме, построенной по выборочным значениям случайного вектора в схеме испытаний Бернулли, можно получить представление о совместной плотности вероятности компонент этого случайного вектора.

8. Приведите пример реальных физических величин, которые необходимо рассматривать как случайный вектор.

4.10. Приложение 1. Полезные функции matlab

1. Размещение на интервала 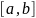заданного числа точек:

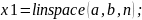
Пример:

>> x=linspace(0, 3, 3)

x =

0 1.5000 3.0000

2. Построение 2-х мерной решетки на плоскости:

Пример:

[X1, X2]=meshgrid(1:1:2, 4:2:8)

Переменная X1 принимает 2 значения: 1 и 2:

X1 =

1 2

1 2

Переменная X2 принимает 3 значения: 4, 6 и 8

X2 =

4 4

6 6

8 8

Все строки массива X содержат все возможные значения пар (X1, X2) на решетке

X=[X1(:) X2(:)]; % Двумерный массив

X’ =

1 1 1 2 2 2

4 6 8 4 6 8

3. Построение поверхности двумерной плотности вероятности

mu=[ 4 3]; % Вектор-строка математических ожиданий компонент.

sigma= [1 -0.4; -0.4 0.25]; % Ковариационная матрица.

[x1, x2] = meshgrid(linspace(0,8,40), linspace(0, 6, 30));

X=[x1(:) x2(:) ];

pd=mvnpdf(X, mu, sigma);

figure(2)

surf(x1, x2, reshape(pd, 30, 40)); % Построение поверхности

Рис. 2. Двумерная плотность вероятности гауссовского вектора

3. Построение поверхности двумерной функции распределения

pc=mvncdf(X, mu, sigma);% Используются данные п. 1.3

figure(3)

surf(x1, x2, reshape(pc, 30, 40));% Используются данные п. 1.3

Рис.3. Совместная функция распределения компонент гауссовского вектора

3. Формирование выборки гауссовского вектора

R=mvnrnd(mu, sigma, n); % mu – вектор-строка математических ожиданий размера 1хd, sigma – ковариационная матрица размера 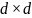. n – объем выборки.

R – выборка значений d-мерного вектора – матрица размера .

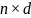3. Построение двумерной гистограммы

figure(4)

hist3(R,[16 12]);% Используются данные п.1.3.

xlabel( ‘ x1’); ylabel( ‘ x2 ‘);

Рис. 4. Гистограмма двумерного гауссовского вектора

Дополнительные сведения о функциях MATLAB, полезных при работе со случайными величинами, можно найти в [3].

4.11. Приложение 2. Выбор вариантов

Таблица 1. Варианты значений параметров двумерной гауссовской плотности вероятностей

№ вар.
		a	b		c		d
1.		0	10		0		10		1.2		0		2
2.		-10	0		-10		0		1.0		0.4		1.2
3.		-10	0		0		10		1.1		0.8		1.42
4.		0	10		-10		0		0.8		0.95		2.01
5.		-5	5		0		10		1.5		1		0.2
6.		0	10		-5		5		1.1		-1		0.25
7.		-5	5		-10		0		1.0		-0.95		1.12
8.		-10	0		-5		5		1.2		-0.85		2
9.		10	20		10		20		1.3		-0.5		2.1
10.		-10	-0		0		10		1.5		0.2		2
11.		-20	-10		-10		0		1.3		0		0.82
12.		-15	-5		-5		5		1.2		0.24		1.3
13.		45	55		45		55		1.17		-0.3		1.28
14.		-55	-45		-45		55		1.09		0		2
15.		45	55		-55		-45		1.6		0.8		1.72
16.		-55	-45		-55		-45		1.21		0.5		0.2
17.		20	30		20		30		1.25		0.2		1.25
18.		30	40		30		40		1.32		-0.5		0.2
19.		-1	9		10		20		1.62		-0.9		2.1
20.		0	10		10		20		1.21		-0.99		2.5
21.		-7		3		-30		-20		1.2		0		2
22.		7		17		0		10		1.72		0.3		2.8
23.		20		30		-30		-20		1.		0.8		2.9
24.		-40		-30		30		40		1.2		-0.5		0.92
25.		-30		-30		20		30		1.01		-0.7		0.2

Номер варианта работы, выполняемого студентом, определяется номером его фамилии в журнале группы.