М . ҚОЗЫБАЕВ АТЫНДАҒЫ

СОЛТҮСТІК ҚАЗАҚСТАН

МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

И.Р. КАСИМОВ

ДӘРІСТЕР КЕШЕНІ

ЖҮЙЕЛЕРДІ ТАЛДАУ ЖӘНЕ ҮЛГІЛЕУ

5B070300 АҚПАРАТТЫҚ ЖҮЙЕЛЕР мамандығы үшін

Петропавл қ.

2 015 ж.

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ

БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛIГI

М. Қозыбаев атындағы

Солтүстік қазақстан Мемлекеттік университеті

5B070300 АҚПАРАТТЫҚ ЖҮЙЕЛЕР мамандығы

И.Р. КАСИМОВ

ДӘРІСТЕР КЕШЕНІ

ЖҮЙЕЛЕРДІ ТАЛДАУ ЖӘНЕ ҮЛГІЛЕУ

пәні бойынша

Петропавл қ.

2015 ж.

Рецензент

Икласова К.Е., аға оқытушы, техника ғылымдарының магистрі.

Құрастырушы:

1. Касимов И.Р., аға оқытушы, техника ғыдымдарының магистрі.

Пәнінің дәрістер курсы 5B070300 Ақпараттық жүйелер мамандығында білім алатын студенттерге арналған. Бұл дәрістер курсының мақсаты осы пәнді меңгеруде студенттерге көмекші құрал ретінде пайдаланылады.

Дәрістер курсы элективті пәндер каталогіна сәйкес келеді, он бес дәріс тақырыптары қарастырылған. Қарастырып отырған сұрақты терең меңгеру мақсатында әрбір дәрістің соңында әдебиетттер тізімі берілген.

Система менеджмента качества СКГУ им. М.Козыбаева

сертифицированана соответствие требованиям ISO 9001:2008

Дәріс 1. Тақырып: Сызықты программалау.

Оптималдандырылған есептер. Сызықты программалаудың әдістер және модельдер. Жоспарлау және басқару есептері.

Жағдай туралы ақпараттың деңгейі бойынша ақпаратты зерттеу мақсатының топтастыруы

1. Детерминирлық деңгей- жағдай туралы ақпараттың ең қарапайым деңгейі –онда шешімді қабылдаған кездегі шарттар толықтай белгілі.

2. Стохастикалық деңгей-онда шарттардың көптеген мүмкін варианттар жиыны белгілі және олардың ықтималды тарату кезеңі.

3. Анықталмаған деңгей- онда көптеген мүмкін варианттар жиыны белгілі, бірақ ықтималдылығы туралы ешқандай ақпарат жоқ. Анықталмаған шарттарда шешім қабылдаудың мақсаттары ойындар теориясын зерттеудің пәні болып келеді.

Өзінің мазмұндық құрылуына байланысты Амал зерттеудің типтік тапсырмалары әртүрлі кластарға бөлінуі мүмкін.

Торлық жоспарлау және басқару мақсаттары ірі комплексті Амалсының аяқталу мерзімін және барлық комплектің басталуының байланысын қарастырады. Бұл тапсырмалар Амал комплексінің жалғастырылуы минималды болуын, бағаның және орындау мерзімін оптималды байланысын шешеді.

Бүқаралық қызмет ету мақсаттары қызмет ету жүйесіне және білуге арналған, онда тапсырыстарды және талаптарды қамтамасыз етеді және қызмет ету уақыты,қызмет ету каналдарының саны мен жұмыс жүйесінің тиімділігі т.б. қарастырылады.

Қорды басқару мақсаттары қор деңгейін және тапсырыс өлшемінің тиімдісін оптималды мәнінін іздейді. Мұндай мақсаттың ерекшелігі мынада, қордың деңгейі көбейген сайын оларды күту үшін көптеген қаражат падаланады, бірақ басқа жақтан өнім қорының дифицит болған жағдайда жоғалтулар азаяды.

Ресурстарды үлестіру мақсаттары анық бір Амал (жұмыс) жинауда пайда болады, оларды шектелген ресурстарда қолдану керек және Амаллар арасында немесе Амаллар құрамы ресурстарының оптималды үлестіруін табу талап етіледі.

Ремонт және құралдарды алмастыру мақсаттары құралдардың ескіруіне және оларды белгілі уақытта жаңаға алмасыруына байланысты актуалды. Тапсырмалар оптималды мерзімге, профилактикалық ремонттың және бақылаудың санына, сондай-ақ құралдарды алмастыру моменттерінің модермизизациясына негізделген.

Кестені құру мақсаттары (күнтізбелік жоспар) Амалды орындауда оптималды реттілік анықтамасы (мысалы, детальдарды өңдеу) әртүрлі құралдарда.

Жоспарлау және тарату мақсаттары оптималды сандар және жаңа объектілерді тарату орындары олардың объектілермен өзара әрекеті анықтамасы.

Маршруты таңдау тапсырмалары немесе тор мақсаттары транспорта әртүрлі зерттеу Амалларда және тор жүйесінде жие кездеседі және экономикалық маршруттар анықтамасында кездеседі.

Амалды зерттеу модельдердің арасында дау жағдайларда оптималды шешімді қабылдау моделдері ерекшеленеді, олар ойындар теориясымен оқытылады. Екі немесе одан да көп жақтың әр түрлі мақсатты көздейтін назары қиылысатын дау жағдайларда экономикалық, заң, әскери жұмыс және т.б. жағынан көптеген жағдайларды жатқызуға болады. Ойындар теориясы тапсырмаларында конфликке қатысқандардың әртүрлі іс-әрекеті жағынан рекомендациясымен танысу және оптималды стратегиясын анықтау қажет.

Амал деп белгілі бір мақсатқа жету үшін әрекеттердің жиынтығы аталады.

Амал жасайтын жақ деп бөлек ұйымдық басшылықпен біріккен және қойылған мақсатқа белсенді ұмтылған (берілген Амалға байланысты) адамдар немесе ұжымды айтамыз.

Амал жасайтын жақтың мысалы берілген период ішінде салалы өндірістің қызметінің сапасын және заманға сай өңдеуін қамтамасыз ететін салалық есептеуіш орталығының (ЕО) қызметкерлері болып келеді.

Амалдың зерттеушісі амал жасайтындар жағынан зерттеу жасайды. Ол да сол мақсатты көздейді, бірақ өзі ақырғы қорытынды шешімін жасамайды, тек ғылыми негізді кепілдемелер, яғни, сапалы және санаулы анализ өткізеді, және басқа бір шешім қабылдаудың жалпы түрін көрсетеді. Қорытынды таңдау және шешім қабылауға Амал жасайтын жақ жауапкершілік әкеледі.

Амал өткізудегі белсенді құралдар деп материалдық, энергетикалық, ақшалы және басқа ресурстардың жиынтығын, сондай-ақ, амал жасайтын жақ амалдың жақсы өтуін қамтамасыз ету және мақсаттарға жету үшін қолданатын мүмкіндіктер ұйымы жатады. Әрине, Амал жасайтын жақ анық бір белсенді құралдардың және оқиғалардың дамуына әсер ететіндей тәуелсіз таңдаы болу керек (кері жағдайда амал басқарылмайтын, ал Амал жасайтын жақ пассивті бақылаушы болады). Амалды зерттеу сферасына әртүрлі ресурстардағы мәселелер тиетіні кездейсоқ емес.

Белсенді құралдардың мысалдары есептеуіш машиналар, электроэнергия, ЕО ұжымындағы уақыт, немесе өндіріс қуаттылығы, шикізат қорларын, заводтың еңбек ресурстарын немесе жұмысшылардың квалификациясы мен құрамына қарай анықтайтын қаржы бөлетін бригаданың өндірістің еңбек ақысының фонды болып келеді.

Амалдың әрекет ететін факторы деп объективті шарттарды және ерекшеліктерін анықтайтын және оның нәтижесіне әсер ететін жағдайларды айтады. Факторларды анықталған (дәл анықталған) және анықталмаған (мүмкін табиғатты немесе парасатты көрсететін) етіп айырады.

Модель және амалдың тиімділігі. Санаулы зерттеу әдістерін қолдану үшін амалдың математикалық моделін құру қажет. Амал моделін құруда, ереже бойынша, оңайланады, жобаланады және Амалдың жобасы қандай да бір математикалық аппарат көмегімен сипатталады. Амалдың моделі- бұл математикалық аппараттың көмегімен амалдың нақты сипатталуы (әртүрлі функциялар, теңдеулер, теңдеулер жүйесі және теңсіздіктер және т.б.). Амалдың моделін құру үшін математикалық аппараттың білімін және сипатталатын құбылыстың мәнін түсіну қажет.

Математикалық модель математикалық символдар көмегімен берілген шынай әлемнің қандай да бір құбылыс классын сипатталуын (кейде жуық түрде) ұсынады.

Амал тиімділігі – тапсырманы орындаудың сәйкестілік дәрежесі – тиімділік критерий түрінде санаулы ұсынылады, яғни, мақсат функциясымен. Мысалы, ресурстарды қолдану тапсырмасында тиімділік критерийі- өңдірілген өнімнің орындалуының пайдасы, оны максимизироваттау керек, ал транспорттың тапсырмада шығынның жиынтығын.

Амалдардың тиімділік критериі деп амалдың мақсаты және қолданылатын әрекеттер нәтижесі аралығындағы қажет ететін, тосатын, соған жететін сәйкестікті айтады. Критеридің негізгі функциясы оларды іске асыру басына дейінгі әртүрлі стратегияны салыстырмалы бағасы болады. Оны Амалдың аяқталатын кезеңінде алынған нәтижелердің сипаттамасы үшін қолданады.

Келешекте амалды зерттеу мақсаттарын құру модельдерінің методологиясын меңгеру маңызды. Амалды сипаттауына кіретін барлық факторларды екі топқа бөлуге болады:

• Тұрақты факторлар (Амалды өткізу шарттары), оларға біз әсер ете алмаймыз. Оларды ,……; деп белгілейік.

• Тәуелді факторлар (шешімнің элементтері) x1,x2,…, оларды біз белгілі шектерде өзіміздің таңдауымыз бойынша таңдай аламыз.

Мысалы, ресурстарды қолдану тапсырмаларында тұрақты факторларға әрбір ресурс қорының түрін апару керек, өндірістік матрицаны, онда элементтер шығарылған өнімнің әрбір түрдің бірлігіне шығын өндірісін анықтайды. Шешу элементтері-өнімді шығарудың әрбір түрінің жоспары.

Мақсаттық деп аталатын кейбір функциямен берілетін тиімділік критерийі екі топтың факторларына тәуелді, сондықтан мақсаттық функцияны Z мына түрде жазуға болады Z=f(x1,x2,…., , …..)

Амалды зерттеудің барлық модельдері табиғатқа және амалдар қасиетіне тәуелді топтастуға мүмкін, тапсырмаларды шешудің сипатталуы, математикалық әдістерді қолдану ерекшеліктері.

Ең бірінші оптимизация моделінің үлкен классын белгілеу қажет. Бұл тапсырмалар жоспарды оптимизациялау және күрделі жүйелерді басқаруда ең біріншіден экономикалық жүйелерде әрекет жасағанда пайда болады. Оптимизациялау тапсырмасын жалпы түрде мына қисынға келтіруге болады: теңсіздік жүйесін(теңдеулер) қанағаттандыратын х1, х₂,…xn, айнымалыларын тауып,

, (0.1)

Мақсат функциясын максимумға (немесе минимумға) жеткізетін, яғни

(0.2)

(Теріс емес айнымалылар шарты, олар бар болса, (0.1) шектерге кіреді).

_п мәнінің жиынының реттілігі х₁, x₂..., х_n айнымалылармен n-шақты кеңістік нүктесімен ұсынылады. Келешекте бұл нүктені Х= (х1, х2, ...,xn), деп белгілейміз, ал оптималды шешудің өзін X* = (х1*, х2*,..., хn*) деп белгілейміз.

f және функциясы (0.1)—(0.2) тапсырмаларында кемінде екі рет дифференциаланған жағдайда, оптимизацияның классикалық әдісін қолдануға болады. Бірақ, осы әдістерді Амалды зерттеуде қолдану шектелген, өйткені n айнымалы функцияның шартты экстримумының тапсырма анықтамасының техникасы өте күрделі: локальді экстримумды анықтауға әдіс мүмкіндік береді, ал функцияның көп өлшемдігіне байланысты оның максималды (немесе минималды) мәнінің (глобальді экстримумы) анықтамасы өте күрделі болып кетуі мүмкін, және де бұл экстримум шешу облысының шекарасында болуы мүмкін. Егер аргументтің мүмкін мәндердің жиыны дискретті немесе Z функциясы кесте түрінде берілсе, онда классикалық әдістер жұмыс істемейді. Бұл жағдайда (0.1)—(0.2) тапсырмаларын шешу үшін математикалық программалау әдісі қолданылады.

Егер тиімділік критерийі Z = f(x₁, x₂, ..., х_n) (0.2) сызықтық функцияны ұсынса, ал

функциясы (0.1) шектеу жүйесінде осылайша сызықтық болса, онда бұндай тапсырма сызықтық программалаудың тапсырмасы болып келеді. Егер мазмұн мағынасынан шықсақ, оның шешуі бүтін сан болу керек, онда бұл тапсырма бүтінсандық сызықтық программалау болып келеді. Бүтін сандарға дейін қарапайым шамалауы мұнда көмек төспейді – жоспар оптималды емес болып кетуі мүмкін. Сондықтан арнайы осындай тапсырмаларды шешу алгоритмін өңдеу қажет, олардың белгілері кесіп тастау ойына негізделген мысалы Гомори алгоритмі болып келеді.

Егер тиімділік критерийі және (немесе) шектеу жүйесі сызықтық емес функциямен берілсе, онда сызықтық емес программалау тапсырмасы болады. Кейде егер берілген функциялар дөңес қасиеттері бар болса, онда тапсырма дөңес программалаудың тапсырмасы болып келеді. Осындай типті тапсырмаларды орындау үшін көптеген сандық әдістер өңделген, олар ЭВМ-да шешіледі, негізінде мақсат функциясының градиент ұғымымен және де градиентке қарсы бағытталса, функция тез кемиді деген негізгі оймен байланысты. Оларға түсу градиент әдісі, қиылысатын градиент әдісі және т.б. жатады. Бірақ, басқа әдістер де бар, олар басқа ойларға негізделген- айып функциясының әдісі, кездейсоқ іздеу әдісінің көптеген варианттары және т.б.

Егер математикалық программалау тапсырмасында уақыт айнымалысы бар болса, және тиімділік критерийі (0.2) айнымалы функциясы сияқты анық емес, жанама-уақыт бойынша Амалдың өтуінің сипатталуын теңдеулер арқылы берілсе, онда бұндай тапсырма динамикалық программалау тапсырмасы болып келеді.

Егер тиімділік критерийі (0.2) және шектеу жүйесі (0.1) функциясы түрінде берілсе, онда геометриялық программалау тапсырмасы бар болады. Егер f және (немесе) функциялары (0.2) және (0.1) берілгенде параметрлерге тәуелді болса, онда параметрлік программалау тапсырмасын аламыз, егер бұл функциялар кездейсоқ сипатталса, онда стохастикалық программалау. Көптеген санаулы шешу варианттарына байланысты егер алгоритмдік жолмен нақты оптимум табу мүмкін болмаса, онда эвристикалық программалау әдісіне келеміз, ол қарастырылған варианттарды қысқартады да оптималды шешуін тауып алмаса да, практика жағынан өте жақсы қанағаттандыратын шешімді табады.

Айтып өткен математикалық әдістің ең үлестірілген және өңделген сызықтық программалау болып табылады. Оның ішіне Амалды зерттеуде кең көлемді тапсырмалар жатады.

Дәріс 2. Тақырып: СБЕ жалпы және каноникалық қойылымдары.

СБЕ жалпы және каноникалық қойылымдары.

Сызықтық программалаудың жалпы есебі.

Қарастырылған есептерде белгісіздердің және қолданылатын қорлар (ресурстар) түрлерінің саны, сонымен қатар нормативті коэффициенттер нақтылы сан мәндерімен сипатталып, сызықты программалау есептерінің математикалық модельдерін құру жолдарының негізгі элементтері көрсетілді.

Осындай есептер негізінде жалпы жағдайдағы сызықты программалау есептерінің математикалық моделдерін тұрғызу жолдарын қарастырайық.

Айталық, өндірілетін өнім түрлерінің саны-n болсын. Егер өнім түрлерінің индексін j-мен белгілесек, онда j=1,2,...n-өнім түрлерінің векторы. Осы өнімді алу үшін пайдаланылатын қорлардың (ресурстардың) санын m деп, ал олардың индексін I-мен белгілейік (I=1,2…m-қорлардың түрлері). Сонымен қатар: a_ij- бір өлшемді j өнімді (затты) алу үшін қажетті I-ші қордың мөлшері, B_i-i-ші қордың қолда бар, өндіріске түсетін мөлшері. C_j - бір өлшемді j-ші өнімнен (заттан) түсетін пайда. X_j табайық деп отырған j-ші белгісіздің мөлшері. Осы қабылданған белгілерді пайдаланып, сызықты программалау есептерінің математикалық моделін былай жазуға болады:

(16)

(17)

(18)

Сонымен (16)-ден (18)-дейінгі өрнек СПЕ-нің математикалық моделінің кеңейтіліп жазылған жалпы түрі.

-мына қосынды белгісін қолданып, әдебиеттерде сызықты программалау есебінің математикалық моделін құрама түрінде былай жазады:

(19)

мына жағдайда:

(20)

(21)

(16) және (19) функцияны мақсат функциясы немесе оптималдық жағдайдың критерийі немесе функционал немесе латынша линеал деп аталады. (17) және (20)- шектеулер жүйелері делінеді. (21)-белгісіздердің теріс болмау шарты деп аталады. (20) және (21) шектеулерді қанағаттандыратын (19) мақсат функцияның экстремалды (максималды немесе минималды) мәнін анықтайтын математикалық қатынастардан құралған өрнекті СПЕ-нің жекеленген математикалық моделі деп аталады.

Жалпы СПЕ-нің моделі құрама түрінде былай жазылады:

(22)

мына жағдайда

(23)

(24)

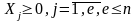(25)

Мұндағы a_ij,b_i және c_j-берілген тұрақты шамалар.

Сызықты программалау есебінің мынадай түрлері:

a)

б)

симметриялы немесе стандартты СП есебі делінеді.

Ескерту: Максимумге ізделінетін есептен, мақсат функцияны минус бірге (-1)көбейту арқылы минимумге өтуге болады, яғни .

Шектеулер жүйесінде тек бір теңдеуде ғана кездесетін коэффициентті (+1) оң таңбалы бірге тең белгісізді базистік белгісіз деп атайды.

СПЕ-нің канондық (КСП) түрде жазылу түрі:

(26)

мына жағдайда

(27)

(28)

КСП есебінің векторлық түрі:

мына жағдайда:

мұндағы C=(c₁,c₂,…c_m),X=(x_1,x_2,…x_n),CX-C және Х векторлардың скалярлық көбейтіндісі. A_j және В –бағана векторлары, олар:

...

КСП есебінің матрицалық түрі:

мына жағдайда

AX=B, X>0

Мұндағы С=(c₁,c₂,…c_т)-бір жолдың матрицасы, А-(a_ij)-өлшемді m*n матрица жүйесі.

-бағана векторы, -бір бағананың матрицасы.

Тәжірибелік есептерде кейде СП матрицалық түрі қолданылады:

,

СПЕ канондық және стандартты формалары.

СПЕ-нің бір түрде жазылуынан екінші жазылу түріне өтуі үшін, біріншіден максимумге ізделетін есепті минимумге келтіреді (немесе керісінше), екіншіден теңсіздіктер-шектеуін теңдіктер-шектеуіне ауыстырады және керісінше, үшіншіден теріс болмау шарты орындалмаған айнымалыны басқа айнымалыларға ауыстыра білу керек.

Мынадай жағдайда

Z =C₁X₁ + C₂Х ₂ + … + C_nX _n min

мақсат функцияны максимумге ауыстыру үшін оны (-1)-ге көбейтеді, яғни

Z₁ =-Z= -C₁X₁ - C₂Х ₂ - … - C_nX _n max

өйткені: min Z  max(-Z)

Алғашқы есептің теңсіздіктер-шектеуі теңдіктер-шектеуіне түрлендіріледі, яғни:

а) алғашқы шектеу а_i1х₁+а_i2х₂ +... + a_inx_nb_i

теңдікке түрлендіргеннен кейін а_i1х₁+а_i2х₂ +... + a_inx_n+x_n+1=b_i немесе

б) алғашқы шектеу а_i1х₁+а_i2х₂ +... + a_inx_nb_i

теңдікке түрлендіргеннен кейін а_i1х₁+а_i2х₂~ +... + a_inx_n-x_n+1=b_i

мұндағы x_n+10

Сонымен қатар шектеулер жүйесінің әр теңдеуін:

а_i1х₁+а_i2х₂ +... + a_inx_n+x_n+1=b_i

теңсіздік түрінде жазуға болады:

Теңсіздіктер-шектеулерін теңдіктерге айналдырғанда енгізілетін қосымша айнымалылардың саны теңсіздіктер санына тең болады.

Қосымша айнымалылар экономикалық тұрғыдан қарағанда мағыналы және олар экономикалық бір мәністі көрсетеді. Оң мәнді қосымша айны-малылар базистікайнымалылар деп те аталады.

Егер Х_к - айнымалы теріс болмау шартына бағынбаса, онда оны екі (U_к және V_к), теріс болмау шартына бағынатын айнымалылармен ауыстырады. Мысалға, X_к =V_к -U_к мұндағы U_кV_к Бір мысал қарастырайық.

1 -мысал. Мына есепті канондық түрде жазу керек.

Z =3Х₁ - 2Х ₂ - 5Х ₄ + X ₅ mах

2-мысал. Алғашқы түрден канондық түрге көшіру керек: Z = 6.2 Х₁ –3.2Х₂ + 4,5Х₃ -> max мына жағдайда

X₁ 0, X₃ 0, 0 X₁ 0

Шешімі. Х₂-айнымалы терісболмау шартына бағынбайды. Сондықтаң оны Х₂ = Х^/₂ – X^//₂, Х^/₂ 0 және Х^//₂  0 , сонымен қатар

X^// ₂ # X^/ ₂. Қабылданған Х₂ қатынасын жүйедегі орнына қойып, мынаны аламыз:

Осыдан кейін жоғарыдағы көрсетілген тәсілдермен есепті канондық түрге көшіреміз:

Есептің канондық түрінен стандартты (біртектес) түріне өту тәсілдерін қарастырайық.

Есептің канондық түрінен стандартты түрге өтудің үш түрлі жолы болуы мүмкін.

1-жағдай. Шектеулер жүйесіндегі әр канондық түрдегі теңдеуде базистік айнымалы бар және барлық базистік айнымалылар мақсат функцияға нөлдік коэффициентпен енгек

2-жағдай. Шектеулер жүйесінде әр теңдікте базистік айнымалы бар, ал мақсат функцияда олар нөлдік коэффициентпен кірмегек

Дәріс 3. Тақырып: СБЕ шешудің геометриялық әдісі.

СБЕ шешудің геометриялық әдісі.

СПЕ шешудің геометрикалық әдісі.

Графиктік әдіс.

Графиктік (геометриялық) әдісті тәжірибелік есептерде пайдалану жағдайын қарастыру үшін математикалық модельді қарастырайық.

(4)

(5)

(6)

математика тұрғысынан берілген есепті шешу дегеніміз (5) және (6) шарттарын қанағаттандыратын (4) функцияның үлкен (кейде кіші) мәнін табу деген сөз. Басқаша айтқанда мәндері (5) және (6) арқылы құралған аймақта (функцияның анықталу аймағы) (4) функция мәндерінің ішіндегі ең үлкенін (кішісін табу керек. Олай болса ең алдымен (4) функцияның анықталу облысынын, (5) және (6) теңсіздіктері арқылы графигін құрастырайық. Ол үшін жазық өсі Х₁ (абциссаны) тік өсі Х₂ (ординатасы) болатын тік бұрышты координат жүйесін тұрғызамыз да, онда 1-теңсіздіктің графигін құрамыз, яғни:

0,6Х₁+0,8Х₂=24 (а)

Бұл сызықты теңдеу (Х₁ мен Х₂ белгісіздерінің дәреже көрсеткіші 1-тең болғандықтан), оның графигі түзу сызық. Ал енді бұл сызықты құру үшін мектеп геометриясының мына теоремасын пайдаланайық: берілген екі нүкте арқылы тек бір ғана түзу жүргізуге болады. Олай болса (а) теңдеуінің графигін салу үшін бізге осы теңдеуді қанағаттандыратын екі нүкте табу қажет. Ең алдымен ОХ₁ өсінің бойында жатқан нүктені табалық. Іздеп отырған нүкте Х₁ өсінің бойында жатқандықтан Х₂-нің мәні нөлге тең. Берілген (а) теңдеундегі Х₂=0 десек, онда 0,6Х₁=24 теңдеуінен Х₁=40 екендігі шығады.

Ал енді ОХ₂ өсінің бойында жататын және берілген (а) теңдеуін қанағаттандыратын нүктені табу үшін Х₁=0 деп аламыз. Егер (а) теңдеуіндегі Х₁-дің орнына нөл қойсақ, онда 0,8Х₂=24 теңдеуден Х₂=30. Табылған Х₁=40, X₂=30 мәндеріне сәйкес нүктелерді осы өстердің бойына орналастырсақ, іздеп отырған екі нүкте табылады. Ал (а) теңдеуінің графигін тұрғызу үшін осы екі нүкте арқылы өтетін түзу жүргіземіз. Біз бұл нүктелерді табуда берілген теңсіздікті теңдеу деп қарастырдық, ал теңсіздікті қанағаттандыратын мәндерін табу үшін табылған түзудің сол жағында жататын нүктелерді ғана аламыз. Графикте осы жағдай қалың сызықтар арқылы көрсетілген.

Жоғарыда айтылған тәсілді пайдаланып, екінші теңсіздіктің (1,2Х₁+0,6Х₂=36) графигін тұрғызамыз да сызықтың төменгі жағын (сол жағын) аламыз. Өйткені екі теңсіздіктің екеуі де “ ” деп берілсе, онда түзу сызықтың үстіндегі (оң жағындағы) нүктелерді қарастырар едік.

Енді графикке және деген мәндерін түсіру керек: Х₂=0 дегеніміз ОХ₁ нүктелер, ал Х₂>0 дегеніміз ОХ₁ өсінің үстінде болады. Сол сияқты теңсіздігі ОХ₂ өсімен оның оң жағындағы нүктелерді көрсетеді. Сонымен біз іздеп отырған есептің анықталу аймағын таптық, ол ОАВС дөңес көп жақтыдан тұрады. Өйткені

X₂

Д 1,2Х₁+0,6Х₂=36

60

0.6X₁+0.8X₂<24

30 А В

С X₂>0

X₁

X₁>0 30 40

Бұл аймақтың барлық нүктелері (5) және (6) теңсіздіктері барлығын қанағаттандырады. Ал ОДС немесе басқа үшбұрышын іздеп отырған аймақ үшін алуға болмайды, өйткені бұл аймақтың АДВ аймағында жатқан нүктелері (5) теңсіздіктер жүйесінің 1- теңсіздігін орындамайды. Сол сияқты СВЕ үшбұрышының нүктелері (5) теңсіздіктер жүйесінің 2-теңсіздігін қанағаттандырмайды. Бұл табылған аймақтың (ОАВС) барлық нүктелеріне сәйкес (4) функциясының мәндері анықталады, ал бұл аймақтағы жатқан нүктелердің саны шексіз болғандықтан Z функциясының да мәндерінің саны шексіз. Есептің мақсаты бойынша шексіз көп мәндердің ішінен біреу ғана ең үлкені болуы мүмкін. Бірақ, шексіз көп (табылған аймақта жатқан) нүктенің ішінен Z-дің мәндерін салыстыру арқылы, функцияның ең үлкен мәнін таңдап алу мүмкін емес.

Алдыңғы тақырыпта келтірілген теорема бойынша, егер сызықты программалаудың (4)-(6) есебінің шешімі болса, ол шешім (5) және (6) шарттар арқылы жасалған дөңес көпжақты төбе нүктелерінде жатады.

Мұндай көпжақтылардың төбелерінің саны шекті, олай болса салыстыру әдісін пайдалануға болады. Біздің есебімізде табылған аймақ төбелерінің саны төртеу, олар О, А, В және С. Бұл төбелерге сәйкес Z-дің мәнін табу үшін олардың координаттарын табайық. О нүктесінде Х₁=0, X₂=0, яғни О(0;0). А нүктесінде X₁=0, X₂=30, демек, А(0;30) және С(40;0). Ал В-нүктесінің координаты бізге белгісіз, ол мына теңдеулердің қиылысу нүктесі:

0,6Х₁+0,8Х₂=24 және 1,2Х₁+0,6Х₂=36.

Демек екі теңдеуді қосып шешу қажет. Өйткені В нүктесінде бұл теңдеулерді шешу үшін 1- теңдеуді (-2)-ге көбейтіп, екі теңдеуді қосамыз:

-1,2Х₁-1,6Х₂=-48

1.2X₁-0.6X₂=36

-X₂=-12, яғни Х₂=12

Егер Х₂=12-ні 1- теңдеуге (немесе 2-теңдеуге) апарып қойсақ нәтижесінде Х₁ аламыз.

0,6Х₁+0,8*12=24; 0.6X₁=24-9.6=14.4

бұдан Х₁=14.4/0.6=247

Демек, В нүктесінің координаттары В(24;12).

Табылған төбелердің координаттарында функция Z-тің мәнін есептеп, олардың ішіндегі максималды мәнді анықтайық:

Z₀=16*0+12*0=0; Z₀=0.

Z_A=16*0+12*30=360 мың теңге

Z_C=16*30+12*0=480 мың теңге

Z_B=16*24+12*12=528 мың теңге

Іздеп отырған функцияның ең үлкен мәні Z=528 мың теңге. Бұл табыс бірінші үлгімен Х₁=24 дана, ал екінші үлгімен Х₂=12 дана киім тігілгенде алынады.

Барлық маталардың қалай пайдаланғанын тексеру үшін Х₁ және Х₂-нің табылған мәндерін (5) және (6) теңсіздіктерге енгізіп есептейік:

0.6*24+0.8*12=14.4+9.6=24.0

1.2*24+0.6*12=28.8+7.2=36.0

Сөйтіп, 1-ші және 2-ші мата толық пайдаланылады және тігін фабрикасына киімді екі үлгімен тіккен тиімді.

Мына шектеулер шарттарын қанағаттандыратын:

және

мақсат функцияның:

Z=1.2X₁+4.8X₂

Максималдық мәнін графиктік әдіспен анықтайық.

Шешімі: Өстері Х₁ және Х₂ болатын тікбұрышты координат жүйесін аламыз да теңсіздіктерді теңдік деп қарап, олардың графигін сызып, сол түзулердің қиылысуынан пайда болған барлық теңсіздіктерге ортақ М анықталу аймағын тұрғызамыз. Табылған М аймағының барлық төбелерінің координаттарын жазайық D(0;200), E(320;0), O(0;0). Ал N және K нүктелерінің координаттары белгісіз, N нүктесі I-ші және II-ші теңсіздіктерді теңдеу деп қарап, олардың бір-бірімен қиылысқан N нүктесінің координатын іздейік, яғни:

0.4X₁+2.0X₂=400; 0.9X₁+1.2X₂=360.

Бұл теңдеулерді шешу үшін I-теңдеуді –0,6-ға көбейтіп II-теңдеумен қосып, мына теңдіктен 0,66Х₁=120, X₁-дің мәнін табамыз (Х₁=181.8=182). Табылған Х₁-дің мәнін екі теңдеудің кез-келген біреуіндегі Х₁-дің орнына қойсақ Х₂ табылады, яғни

0,4*182+2Х₂=400, X₂=163.6=164.

10х₁+4х₂=3200

D

0.1x₁+1.2x₂=360 N

K

M

O E

0.4x₁+2x₂=400

Сонымен N нүктесінің координаттары 182 және 164 тең, яғни N(184;164).

Енді K нүктесінің координаттарын табу үшін II-ші және III-ші теңдеулерді қосып шешеміз:

0,9X₁+1.2X₂=360

10X₁+4.0X₂=3200

X₁=286, X₂=85 болады, демек (286;85). Бұл төбелерге сәйкес мақсат функцияның мәндерін есептейік.

1. О(0,0)-бұл төбедегі есептің экономикалық мәні былай түсіндіріледі, үш станоктың үшеуі де әлі жұмысқа қосылмаған, сондықтан ешбір өнім (зат) шығарылмаған, олай болса өнімнен келетін пайда нөлге тең.

Шынында да:

Z₀=1.2*0+4.8*0=0.

2. D(0;200)-мұнда Х₁=0, X₂=200, демек, бірінші зат өндірілмейді, тек екінші заттан 200 дана жасалынады. Бұл кезде мақсат функцияның мәні: Z_D=1.2*0+4.8*200=960 мың теңге. Станоктардың уақыттары қалай пайдаланатындығын қарастырылған (1-топтағы станоктың уақыты толық пайдаланылады, 2-топтағы станоктардың 120 сағат уақыты, ал 3-топтағы станоктардың 2400 сағат уақыты пайдаланылмай қалады).

3. Е(320;0) –бұл жағдайда Х₁=320, X₂=0, демек 2-зат өндірілмейді, ал 1-заттан 320 дана жасалынған. Бұл жағдайда мақсат функциясы Z_E мәні 384 мың теңгеге тең (3-топтағы станоктар толық пайдаланылады, ал 1-топтағы станоктардың 72 сағат уақыттары пайдаланылмай қалады).

4. N (182;164)-бұл жағдайда Х₁=182 және Х₂=164.

1-топтағы (0,4*182+2*164=400) және 2-топтағы (0,9*182+1,2*164=360) станоктардың уақыт қоры толық пайдаланылады, ал 3- топтағы станоктардың (10*182+4*164=2476) сағат уақыты ғана пайдаланылады да 724 сағат уақыты пайдаланылмай қалады.

5. К (286;85) демек Х₁=286, X₂=85 дана, бұл жағдайда мақсат функцияның мәні Z_k=751.0 мың тең болады, ал 2 және 3-топтағы станоктар толық пайдаланылады. 1-топтағы станоктардың 116 сағат уақыты пайдаланылмай қалады. Енді осы Z₀,Z_D,Z_N,Z_K,Z_E –лердің мәндерінің ең үлкенін алу керек, ол Z_N=1005.8 теңгеге тең, бірақ бұл жағдайда 3-топтағы станоктардың 724 сағат уақыты артылып қалады.

Менеджер, есептің шығару нәтижесін талдай келе мынадай: 3-топтағы станоктардың артығын сатыға немесе уақыттары осы уақытқа сәйкес келетін 1 немесе 2 – топтағы станоктарды сатып алып жұмыс орнын кеңейтуге шешім қабылдай алады. Соңғы шешім қосымша уақытқа сәйкес тағы да пайда түсіруі үшін қабылдануы мүмкін. Пайдаланылмаған станок уақыт ескерусіз қалса, кәсіпорын 1005,8 мың теңге зиян шегуі мүмкін. Себебі 724 сағатқа сәйкес техниканың жұмыссыз тұрған уақыты және жұмыскерлер шығыны ескерусіз қалып отыр.

Z=140X₁+640X₂ max

шектеулер теңсіздіктері:

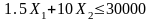
Шешімі. 1. Анықталу аймағын құрамыз. Төбелердің координаттары: О(0;0), А(0;2750), D(9000;0), ал В-ның координатын табу үшін 2 және 3- теңдеулерді бірге қарастырып: Х₁=2250, X₂=5000, яғни В(5000;2250) және С нүктесінің координаттарын табу үшін 1 және 3-теңдеулерден: Х₁=7059, X₂=1941, яғни С(7059;1941) алдық. Енді осы нүктелердегі мақсат функцияның мәндерін анықтайық:

Х₂

А

В

О Д 10000 20000 30000 Х₁

1. О(0;0) нүктеде мақсат функция Z₀=0.

2. A(0;2750) нүктесінде қант қызылшасына 2750 гектар бөлінеді, еңбек күні толық пайдаланылады, 6250 гектар жер көлемі және 2500т миниралдық тыңайтқыштар артылып (қолданылмай) қалады. Бұл жағдай Z_A=1760 мың теңге пайда береді.

3. D(9000;0)-X₁=9000, X₂=0, олай болса Z_D= 140*9000=1260 мың теңге пайда түседі. Бұл жағдайда жер көлемі толық пайдаланылады да, 74 мың еңбек күн және 16,5 мың т миниралдық тыңайтқыш артылып қалады.

4. В(5000;2250) демек бидайға 5000, қант қызылшаға 2250 гектар жер бөлу керек, бұл жағдайда минералдық тыңайтқыш және еңбек күні толық пайдаланылады, ал егістік жердің 1750 гектар пайдаланылмай қалады. Алатын пайда (мақсат функциясы);

Z_B=140*5000+640*2250=2140.0 мың теңге болады;

С(7059;1941), демек 7059 гектар жерге бидай, 1941 гектар жерге қант қызылшасын егу қажет, алынатын пайда Z=2230.5 мың теңгеге тең, бұл жағдайда 4117 еңбек күні артылып қалады. Сонымен, егер жердің 7059 гектарына бидай, 1941 гектар жерге қант қызылшасын егіп өндіргенде шаруашылық2230,5 мың теңге ақша алады. Бұл пайда қарастырылған жоспарлардан түсетін пайдадан әлде қайда көп және қолда бар қор дұрыс пайдаланылады. Демек, есептің оптималды шешімі табылады. Жоғарыда графиктік әдіспен ШМБА-ң әр төбелері координаттарының мәнін аналитикалық геоиетрия тәсілімен тауып және осы мәндерде мақсат функцияның мәндерін есептейік. Нәтижесінде алынған мақсат функцияның мәндерін бір-бірімен салыстыра отырып, оның экстремалдық мәнін анықтайық.

Төменде жоғарыда баяндалған СПЕ-н графиктік әдіспен шығарудың ұтымды алгоритмі қарастырылады.

Графиктік әдіспен СПЕ шығару алгоритмі.

1. Шектеулер жүйелерінің шешімі мүмкін бола алатын (ШМБА) аймақты анықтайды.

2. Вектор-градиентті (с) тұрғызады.

3. Вектор-градиентке тікбұрышпен (перпендикуляр) деңгей сызығын жүргізеді (Z₀).

4. Егер мақсат функция максимумге ізделінсе, онда вектор-градиенттің бағытымен, ал егер мақсат функция минимумге ізделінсе кері бағытпен деңгей сызығын өзіне-өзін параллель жылжытады.

5. Деңгей сызық ШМБА-ның жалғыз ғана (егер Z max ұмтылса, онда “шығу”, егер Z min ұмтылса, онда “ену”) нүктемен жанасқанша өзіне-өзі параллель жылжыта беріледі. Осы жанасу нүктесі СПЕ-ң жалғаз ғана шешімін береді және ол экстремалды нүкте болып есептелінеді.

ЕгерШМБА-ның бір қабырғасына деңгей сызығы параллель болса, онда осы қабырғаның барлық нүктелерінде мақсат функцияның экстремалды мәне алынады. Сөйтіп СПЕ –нің шексіз көп шешімдері болуы мүмкін. Мұндай СПЕ-нің альтернативті оптимумы болады деп айтылады және оның шешіміш мына формула арқылы табады:

,

мұндағы және -ШМБА-ның бұрыштық нүктелерінің оптималды шешімі.

Егер шектеулер бір-біріне қайшы болса СПЕ шешілмейді.

Экстремальды нүктенің координаттарын тауып, осы координаттардағы мақсат функцияның мәнін есептейді.

Бір мысал қарастырайық.

Мысал.

Осы жағдайда мына мақсат функцияның:

Z=X₁+X₂

максималды және минималды мәнін анықтайық.

Шешімі: Жүйедегі барлық теңсіздіктерді теңдік түрінде жазамыз.

( а)

(в)

(г)

(д)

(е)

Кординаттар жүйесінде алынған түзілерді тұрғызамыз да, шектеулер жүйелерінің ШМБА –ын анықтаймыз.

Есептің ШМБА-ы үшбұрышы. Осы АВС үшбұрышы есептің барлық шартын қанағаттандырады.

векторын тұрғызамыз. Бұл вектордың соңғы нүктесінің координаты мақсат функцияның белгісіздерінің кооэффициенттеріне сәйкес. Олай болса (1,1).

векторына тікбұрышты деңгей сызығын жүргіземіз. Осы деңгей сызықты вектордың бағытымен өз-өзіне параллель жылжыта отырып, оның ШМБА-н ең ақырғы жанасу нүктесі С бұрышы екенін анықтадық, яғни осы нүктеде мақсат функция Z-өзінің өзінің максималды мәніне жетеді.

С-нүктесі а) және г) түзулерінің қиылысында жатыр, яғни мына жүйеден:

және Х₂=3 екенін таптық. Табылған мәндерді мақсат функцияға жазып, оның минималды мәнін анықтадық: .

Сонымен әртүрлі СПЕ-н графиктік әдіспен шешу жолын талдай келе мынадай қорытындылар жасауға болады:

-екі айнымалы СПЕ-н шешу аймағы шектелген дөңес көпбұрыш немесе шектелмеген көп қырлы аймақ;

-егер СПЕ-ң тиімді шешімі болса, онда оған шешімі мүмкін бола алатын аймақтың бір төбесінде жетуге болады.

-егер СПЕ-ң шешімі болмаса, онда оның себебі: а) жүйедегі шектеулердің бірлеспегендігінен; б) мақсат функцияның шектелмегенінен.

Дәріс 4. Тақырып: СБЕ шешудің симплекстік әдіс.

СБЕ шешудің алгебралық симплекстік әдіс.

Қысқаша симплекс әдісінің шығу тарихы

Жалпы математикалық программалау пәні өмірдің қажеттілігінен пайда болған қолданбалы математиканың ең негізгі бөлімі. Математикалық программалау пәнінің ең негізгі бөлімі сызықты программалау есептері дүние жүзінде бірінші рет 1930 жылдары жарық көрді. Сызықты программалау есептері басқа тәжірибелік есептерге қарағанда өте қарапайым, зерттеуге ыңғайлы.

Сызықты программалаудың дербес есебінің бірі - қатынас есебінің дербес түрі 1931 жылы Венгрияда басылып шықты, бұл мақаланың авторы математик Эгервари болатын. Кейінірек келе бұл мақаланың негізінде бірнеше еңбектер жазылды. Бұған мысал үшін 1951 және 1956 жылдары жарыққа шыққан Кун X. В. және Таккер А. В., 1957 ж. жазылған Форд X. Р. және Фалкерсон Д. Р. еңбектерін алуға болады. Бұл еңбектерде қатынас есептерін шешуге арналған әдістер көрсетілгең кейін келе әдебиеттерде бұл әдісті қатынас есептерін шешудегі Венгер әдісі дейтін болды. Сызықты программалау атты термин алғаш рет 1940 жылдары АҚШ-та қолданылды. Сызықты программалау әдісінің арнайы есептерінің бірі 1941 жылы АҚШ-та басылып шықты, оның авторы Хичкок Ф. Л. болатын.

Бұрынғы Кеңестер Одағында сызықты программалау әдісінің негізін қалаушы академик Л. В. Канторович болды. Себебі оның көптеген сызықтық программалау әдістеріне арналған дербес есептері 1930 жылдардан бастап жарыққа шыға бастады. 1956 жылы Дж. Данциг, X. Р. Форд және Д. Р. Фалкерсон Венгер әдісінің негізінде сызықты програм-малаудың есептерін шешуге арналған, Л. В. Канторович ұсынған потенциал әдісіне өте сәйкес әдіс ұсынды. Ал 1947 жылы Дж. Б. Данциг сызықтық программалау әдістерінің ішіндегі әмебап симплекс әдісін жарыққа шығарды. Бірақ бұл әдістің Л. В. Канторовичтың 1939 ж. ұсын-ғаң біртіндеп жақсарту әдісінен айырмашылығы өте аз болатын. Өкінішке орай бұл әдісті Л. В. Канторович бұрын ұсынса да көптеген әдебиеттерде, оқулықтарда симплекс әдісін Дж. Данциг әдісі деп атайды.

Симплекс әдісінің геометриялық түсінігі

Симплекс-ағылшын сөзі, кеңістіктегі қарапайым көпбұрышты көп жақты бейне, оның бұрыштарының координаттары ізделініп отырған белгісіздердің оптималды мәндеріне сәйкес. Көп өлшемді геометрияда: Х₁+Х₂+...+Х_n=1, шарттарын қанағаттандыратын А (X₁, Х₂,…,Х_n) нүктесінің геометриялық орны симплекс делінеді.

Симплекс әдісінің негізгі мақсаты - егер мақсат фунция максимумге ізделінсе, онда алғашқы табылған төбеден келесі төбеге жылжығанда кез келген төбеге емес, мақсат функцияның мәні өсетін төбеге ғана жылжуды қамтамасыз ету. (Егер есеп минимумге ізделінсе, онда алғашқы мақсат функцияның мәнінен кейінгі мәні кіші болуын қамтамасыз ету).

Сонымең симплекс әдісін қолданғанда бір төбеден екінші төбеге көшкенде белгілі бір бағытта жоспарлы түрде көшіледі, бұл жағдайда кейбір "керексіз" көпжақтының төбелері қарастырылмай қалып қалады да, есептің шешу жұмысы ұтымды, жедел жүргізіледі. Симплекс әдісін графиктік жолмен іске асырғанда осы айтылған жағдайларды графиктен көзбен көруге болады. Бірақ мұндай жұмыстар белгісіздердің саны үштен көп болғанда қиындайды да, тіпті оларды орындау мүмкін емес. Мұндай кездерде тек ойша тұжырымдарға ғана сүйенуге тура келеді. Сонымен қатар графиктік жолмен шығатын есептердің тәжірибелік есептерге қарағанда мүмкіндіктері аз, маңызы және мәнісі төмен. Сондықтан сызықты программалау есептерін симплекс әдісімен шешудің математикалық алгоритмдерінің маңызы үлкен.

Симплекс әдісінің алгоритмі

Симплекс әдісінің мақсаты мен идеясын толық түсіну үшін есепті жалпы түрде қарастырып, әдісті тәжірибелік есептерге қолдану жолын қарастырайық. Ол үшін ең алдымен сызықты программалау есептерінің жалпы моделінің мәнісіне тоқталайық. Төмендегі шектеуші шарттарды қанағаттандыратын:

(1)

(2)

Мына мақсат функцияның ең үлкен (оптималдық) мәнін табу керек делік:

(3)

(1) және (2) теңсіздіктер берілгендіктен математика тілінде есептің анықталу аймағы берілді деп есептейміз. Ал енді бізге оптималдық төбеге қарай жылжу үшін ең алдымен есептің барлық шектеуші шарттарын орындайтын алғашқы шешуді табу керек. Ол үшін (1) теңсіздіктердің әрқайсысының сол жағына Y_i(i=1,2...m) санын қосып теңдікке айналдырамыз.

Экономикалық мағынада У₁,У₂,...,У_m-дер сәйкес 1,2,... және т -қордың қолданылмаған (өндіріске түспеген) мөлшерін береді. Егер есепті шешу нәтижесінде У₁= 0, У₂= 0, ..., Уm= 0 болса, онда барлық қорлар толығымен өндірісте қолданылған. Бірақ іс жүзінде барлық қордың берілген мөлшері бірден толық пайдаланбауы да мүмкін. Ал У₁,У₂,...,У_m - пайдаланылмаған қор мөлшерін беретіндіктен өндіріске еш пайда келтірмейді, демек мақсат функцияда олардың (У₁,У₂,...,У_m) коэффициенттері нөлге тең болады, яғни:

Сонымең есеп (1) және (2) шарттар орындалған жағдайдағы (3) функцияның ең үлкен мәнін беретін шешуді іздеуге бағытталған. Егер (1) теңцікті Y_i(i=1,2...m) арқылы шешетін болсақ:

(4)

Мұндағы Y₁,Y₂,…,Y_m белгісіздері математика тілінде базистік белгісіздер деп, ал Х₁, Х₂,…,Х_п- базистік емес белгісіздер деп аталады. Демек базистік белгісіздер (векторлар) базистік емес белгісіздер арқылы өрнектеледі. Егер Х = 0, Х₂= 0,..., Х_n = 0 десек, (4) теңдеуден Y₁ =b₁,Y₂=b₂,…,Y_m=b_m.

Экономикалық мағынасы b_i, (i= 1,2,..., m) қолда бар қордың мөлшері болғаңдықтан әрқашаңда , (i=1,2,...,m), ендеше деген жағдай (1) және (2) теңдеулерінің шешімін береді, бұл жағдайда мақсат функцияның мәні нөлге тең (Z=0), өйткені әлі ешқандай өнім өндірілген жоқ. Олай болса, шешу жағдайы есептің алғашқы шешімі бола алады. Демек, алғашқы шешімі табылды, енді мақсат функциясының мәні кемімейтін келесі төбеге көшу керек.

Ол үшін біз оны кесте түрінде түсіндірелік. Ақырғы теңдеулер арқылы алғашқы симплекс - кесте құрылады. Кестеде 1-ші жолға әр тік графаларға негізгі айнымалылардың белгілері және соңғы тік графаға босмүшелердің белгісі жазылады. Сонымен қатар, бірінші жолдың сол жағындағы бірінші торда №-белгісімен әр "Итерация"-ның симплекс кестесінің реттік нөмірі көрсетіледі. 1-ші бағанаға әр жатық графаларға базистік айнымалылардың белгілері, ал ақырғы жатық графаға мақсат функцияның белгісі жазылады. Кесте айнымалылардың коэффициенттермен бос мүшелермен толтырылады, яғни өздерінің орындарына сәйкес торларға жазылады. Симплекс кестесінің соңғы жолын индекстік немесе мақсат функцияның жолы деп атайды.

Кесте-1

Есепті шешуді симплекс кестені талдаудан бастайды, яғни шешуші бағананы, шешуші жолды және шешуші элементті анықтайды. Бұл көрсеткіштерді бағыттаушы бағана, бағыттаушы жол және бас элемент деп атайық. Симплекс кестені талдау - бағыттаушы бағананы анықтаудан басталады. Есепті шешу мынадай алгоритм бойынша жүргізіледі:

1. т+1 жолдың теріс таңбалы элементтері (-С_j) ішінен абсолюттік шамасы ең үлкенін таңдайды (4.1-кесте):

Осы бағана бағыттаушы бағана деп аталады да k-мен белгіленеді. Бағыттаушы бағананы табудағы мақсат, негізгі белгісіздердің ішіндегі базиске енетінін анықтау. Олай болса, Х_k базистік белгісіздердің қатарына енетіні. Геометрияның заңы бойынша базистың саны берілген теңдеу саны m-нен артпау керек, ендеше базистік белгісіздердің бірі базистық құрамынан шығып Х_k-нің орнына бару керек, былайша айтқанда олар өзара орын ауыстырады. Орын ауыстырудан бұрын базистік белгісіздердің құрамынан шығатын белгісізді анықтайық.

2. Бос мүшелер бағанасындағы (b_i) базистік белгісіздердің жолында жатқан әр санды бағыттауыш бағанасында (k) орналасқан элементтерге бөледі де ішіндегі ең кіші бөліндіні (міндетті түрде бөлінді әрқашанда оң сан болу керек) анықтайды, яғни:

демек ең кіші қатынас г-ші жатық жолда жатыр екен делік, онда г-ші жатық жолды бағыттауыш жол деп атайды. Бағыттауыш бағанамен бағыттауыш жолдың қиылысуында жатқан элементті бас элемент деп атайды да a_rk мен белгілейді. Бағыттаушы жатық жолдың нөмірі r-мен белгіленеді де, У_r-базистік белгісіз базистан шығарылатыны анықталынады.

3. Енді Х_к мен У_r -дің орындарын ауыстырып, жаңа кесте тұрғызу жолын қарастырайық, яғни бір базистен екінші базиске және m+1 жатық жолдары бар жаңа матрица құруымыз керек. Мұндағы негізгі матрицаны А деп белгілесек, онда А матрицасының өлшемі (т х п) элементтен тұрады. Ал егер А матрицасына соңғы бос мүшелер бағанасын b₁,b₂,…b_m қоссақ, ондағы шыққан матрицаны кеңейтілген матрица дейді де, А¹ арқылы белгілейді. Осы матрица жөніндегі түсініктен кейін 1-кестені пайдаланып, бір базистен екінші базисқа көшу жолын қарастыралық. Ол үшін ең алдымен шешімнің оптималды шартына түсініктеме берейік, яғни былайша айтқанда оптималды төбеге жеткенімізді қалай білеміз?

Сызықты программалау есебінің оптимапдық шарты жөнінде мынадай теорема белгілі: егер мына жағдайда Z —> max табылған шешімде (мысалы Ү_i =b_i> 0, С_j = 0) мақсат функцияның коэффициенттері С_j, яғни соңғы m+1 жатық жолдың (бос мүшелер бағанасындағы элементті қоспағанда) барлық элементтері оң болса (мына жағдайда Z—> min, керісінше барлық элементтер теріс болуға тиіс), онда осы шешім оптималды делінеді.

Жоғарыдағы теоремада берілген оптималды шешімнің шарты бойынша 1-кестедегі шешім (Ү_i =b_i> 0, X_j = 0, j=1..n) оптималды шешімді бермейді, себебі мақсат функцияның коэффициенттерінің барлығы теріс таңбалы сандар (-С_j < 0).

Симплекс әдісінің негізгі мақсаты бастапқы шешімді (жоспарды) бірте-бірте жақсарта отырып, ең пайдалы (оптималды) жоспарға жету.

Матрицаның (кестенің) жаңа элементтерін мынадай формулалармен есептеуге болады:

1. Бас элементтің орнындағы жаңа элемент:

(осы формуламен табылған бас элементтің жаңа мәнін жаңа кестеге бас элемент тұрған жерге жазамыз).

2. Жаңа кестедегі бағыттаушы жолға сәйкес жолдың элементтерін (Х_к - бойынша шешілген теңдеуден табылған) мына формуламен

мұндағы а_ri-алдыңғы кестедегі бағыттаушы r-жолының элементтері {j= 1,2,... n + 1); а_rk - бас элемент.

3. Жаңа кестедегі бағыттаушы бағанаға сәйкес бағананың элементтері мына формуламен есептелінеді:

мұндағы а_ik -алдыңғы кестенің бағыттаушы k-бағанасының элементтері (i = 1,2,..., т + 1).

4. Матрицаның (жаңа кестенің) қалған элементтерін (жоғарыдағы теңдеулер жүйесіне сәйкес) мына формуламен есептейміз:

Осы формуладағы

деп алып, оны былай түрлендірсекжаңа кестенің қалған элементтерін есептеу әрекеттері біраз жеңілденеді, яғни:

5. Тұрғызылған жаңа кестенің оптималды шартын тексереміз, басқаша айтқанда m +1 -жолындағы элементтердің (b_i - бағанасындағы элементтен басқа) ішінде теріс таңбалары бар ма? Жоқ па? (Z = mіn болған жағдайда, керісінше):

а) егер m+1 жатық жолды барлық элементтері оң сандар (С¹_j >=0) болса, онда (Z = max болған жағдайда) есеп шешімін тапты. Белгілері базис бағанасында жазылған белгісіздердің мәндері өздеріне сәйкес жолдан b_i - бағанасынан алынады да, ал мақсат функцияның мәні сол бағанадан ақырғы жолдан алынады.

б) егер m + 1 жатық жолдың элементтерінің ішінде әлі теріс таңбалары болса, онда жоспарды әлі де жетілдіруге болады, ол үшін 1-4 пункттерде келтірілген әрекеттерді барлық С¹_j оң, не нөл болғанша қайталаймыз. Егер есептің шешуі болса, онда біраз итерациядан кейін а) жағдайына келеміз, демек есептің шешуі табылды деген сөз. Егер олай болмаса, есептің шешуі болмайды, былайша айтқанда есеп дұрыс құрылмаған (шектеуші шарттар дұрыс қойылмаған немесе белгісіздердің коэффициенттері а_ij, b_i дұрыс табылмаған деп шешім қабылданады) есептің қойылуын және математикалық моделінің құрылуын қайта тексеруге тура келеді.

Дәріс 5. Тақырып: СБ екі мағыналы есеп.

СБ екі мағыналы есеп. Екі мағыналы симплекс әдіс.

Тәжірибелік есептерді симплекс әдісімен шығару

Біз алдыңғы тақырыпта симплекс әдісінің жалпы алгоритімін қарастырдық, енді осы алгоритмді пайдаланып, бірнеше тәжірибелік есептерді шешіп, оған талдау берелік.

Жоғарыдағы тақырыпта сан мәнінде қарастырылған мысалға симплекс алгоритмін қолданайық. Төмеңдегі шектеуші шарттарды қанағаттандыратын

(5)

(6)

мына мақсат функцияның ең үлкен мәнін табу керек:

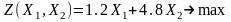(7)

Симплекс әдісінің алгоритмі бойынша (5) теңсіздіктердің сол жағына қосымша оң белгісіздер қосу арқылы теңдікке айналдырамыз:

( 8)

(9)

Экономикалық мағынада у₁, у₂ және у₃ қолданылмаған станоктардың уақыты. Олай болса у₁, у₂ және у₃ өндіріс орнына ешбір паида келтірмейді, былайша айтқанда пайдасы нөлге тең, демек:

(10)

Сонымең біз (5) - (7) есептің орнына (8) - (10) есебін шешетін болдық. Егер (8) теңдеуін у₁, у₂ және у₃ арқылы шешетін болсақ:

(11)

Мұндағы X₁= 0, Х₂= 0 десек, онда у₁ = 400, у₂= 360, у₃= 3200 болады, бұл сандар (8) - (10) теңдіктерін толық қанағаттандырады, ендеше бұларды алғашқы шешім ретінде қабылдауға болады. Бұл жағдайда Z (X₁, X₂) = 0 болады. Есептің мақсаты бастапқы жоспарды (алғашқы базистік шешімді) бірте-бірте жақсарта отырып, ең пайдалы жоспарға жету. Симплекс әдісі бойынша есептің шешімін симплекс кестелер арқылы іздеген өте тиімді. Сондықтан (10,11) жүйелердің коэффициенттері арқылы кесте құрамыз:

Кесте-2

Бұл кестедегі жоспар оптималды жоспарды (шешімді) бермейді. Өйткені, есеп мақсат функцияның үлкен мәнін табуға беріліп отыр, ал кестедегі соңғы жолдың (Z - функциясының коэффициенттері) элементтері (-1,2; -4,8) теріс таңбалы. Бұл жоспарды жақсартуға болады, ол үшін бір базистік белгісізбен базистік емес белгісіздердің орындарын ауыстырамыз, яғни бір базистік белгісіздермен екінші базистік белгісіздерге көшеміз. Базистік емес белгісіздердің қайсысы базиске ену керек екендігін білу үшін, соңғы жатық жолдың теріс элементтері ішінен ең кіші элементті іздейміз (абсолют шамасы бойынша ең үлкенін).

max(|-1,2|, |-4,8|) = -4,8

бұл сан 2-ші бағанаға сәйкес, ендеше бағыттау бағана ретінде k= 2 аламыз, демек Х₂ базиске енеді.

Базистың құрамынан шығатын базистік белгісізді анықтайық.

Ол үшін

Бұл қатынастардың ең кішісі 1 -ші жатық жолда жатыр, демек бағыттаушы жатық жол r= 1 болады да, X₁, мен у₁, орындарымен ауысатыны анықталды. Олардың орындарын ауыстырғанда жаңа базиске сәйкес матрицаның барлық элементтері өзгереді. Оларды төмендегі алгоритм арқылы өзгертеміз де, келесі кестеге сәйкес орындарға жазамыз.

Бағыттаушы бағана (х₂) мен бағыттаушы жолдың (у₁) қиылысында тұрған элемент бас элемент деп аталатыны белгілі, олай болса бұл элемент а_rk, немесе а₁₂= 2. Осы әрекеттерден кейін жаңа тұрғызамыз (3-кесте). Төменде жаңа кестенің элементтерін анықтау алгоритмі келтірілген.

1. 

   Бас элементтің орнында тұратын жаңа элемент:

2. Бағыттаушы жатық жолға сәйкес жолдағы элементтер:

3. Бағыттаушы бағанаға сәйкес бағанадағы элементтер:

4. Жаңа кестенің қалған элементтері мына формула арқылы анық-талады:

Осы табылған элемент аркылы жаңа кесте құрылады (4.3-кесте).

Кесте -3

Сонымен жаңа базистік белгісіздер:

Х₂= 200, у₂= 120, у₃= 2400 бұл жағдайда мақсат функцияның мәні Z= 960 мың теңге болады. Алынған базистік шешімнен неге жеткенімізді баяндайық. Екінші заттан 200 дана жасау керек, бұл жағдайда өндіріс орны 960 мың теңге пайда табады, ал екінші топтағы станоктардың 120 сағат, үшінші топ станоктарының 2400 сағат уақыты пайдаланылмай қалады. Табылған жоспар оптималдық шешімді бермейді, себебі соңғы индекс жолындағы элементтер ішінде әлі де болса теріс таңбалысы бар. Табылған кестеге жоғарыдағы әдісті қолдансақ жаңа кесте аламыз:

Кесте 4

Жаңа базис Х₂= 160, X₁ = 200, у₃= 560. Бұл жағдайда мақсат функциясының мәні Z = 1008 мың теңге, жоспар оптималды, өйткені соңғы жатық жолдың (мақсат функцияның коэффициенттері) барлық элементтері оң сандар. Сонымең оптималды шешім бойынша 1-ші заттан Х₁ = 200 дана, 2-шісінен Х₂=160 дана жасау керек. Бірақ 3-ші топтағы станоктарды 560 сағат уақыты пайдаланылмай қалады. Егер өндіріс орны шынында да 1008 мың теңге пайда табу үшін 3-ші топтағы станоктардың (560 сағатқа сәйкес келетін) біразын сатып немесе басқа жұмысқа пайдалғандары жөн Ал өндіріс көлемін кеңейткісі келсе, онда (3-ші топтағы станоктардың 560 сағаттық жұмыс уқытына сәйкес) 1-ші және 2-ші топтардағы станоктарға қосымша станоктар сатып алу керек. Сонымең өндіріс орнының бар қорларды пайдалана отырып қандай заттан қанша өндіргенде көп пайда таба алатынын білдік.

М-әдісі (жасанды базис әдісі)

Өткен тақырыпта біз есептің математикалық моделіндегі шектеуші теңсіздіктердің тек кіші не тең болған (< ) жағдайын қарастырдық. Ал ендеше бұл шарттар үлкен не тең (> ) болып келсе, онда жоғарыдағы қарапайым симплекс әдісін бірден қолдануға болмайды. Мұндай есептер үшін арнайы әдіс қолдануға тура келеді. Мына (12) және (13) шектеуші шарттарды қанағаттандыратын:

( 12)

(13)

(14)

Мақсат функцияның экстремальдық мәнін беретін X₁,..., Х_n белгісіздер мәнін табу керек. Бұл есепке симплекс әдісін пайдалану үшін қосымша X_n+1,..., Х_n+m белгісіздерін(12) теңсіздіктер жүйесінің әр теңсіздіктердің сол жағынан алып тастау арқылы оларды теңдікке айналдырамыз, яғни канонды түрлендіреміз. Осындай әрекеттен кейін (12) теңсіздіктер жүйесі мына түрге келеді:

(15)

(16)

Шектеуші шарттарын қанағаттандыратын мына

(17)

мақсат функцияның ең үлкен мәнін беретін Х₁ Х₂ Х_n белгісіздердің мәнін табу керек.

Егер (15) теңдіктерін қосымша х_i -лер арқылы шешсек, онда:

(18)

аламыз. Жоғарыда пайдаланылған тәсіл бойынша алғашқы базистік белгісіздерді табу үшін негізгі белгісіздерді нөлге теңестіреміз, яғни

Х_j= 0,j=1,2, ...n,

онда барлық қосымша белгісіздердің мәндері

теріс сан болады. Мұндай жағдай есептің (16) шартына қарсы, яғни базистік белгісіздер теріс болуы мүмкін емес. Сөйтіп алғашқы базистік шешім болмағандықтан мұндай есепті шешуге қарапайым симплекс әдісті қолдануға болмайды.

Есепті симплекс әдісімен шығару үшін (15) теңдіктер жүйесіне жасанды базистік белгісіздерді (у₁, у₂, ...у_n) енгіземіз. Олар мақсат функцияға М - коэффициентімен енеді. Осыдан кейін М есебі құрылады. М - коэффициенті алдын ала белгісіз сан. Егер Z-> max болса, онда ол өте үлкен теріс сан "-М", ал егер Z -> min болса, онда ол өте үлкен оң сан "+М".

М-есебінің ерекшелігі, оның әрқашанда тірек шешімі бар. Енді осы айтылған әрекеттерді жоғарыдағы есепке қолданайық.

(19)

(20)

Мақсат функцияның ең үлкен (ең кіші) мәнін беретін Х₁ Х₂,... Х_n-дi табу керек:

Z= С₁Х₁+С₂Х₂+...+С_nХ_n+0Х_n+1+0Х_n+2+...+0Х_n+m +М(у₁+у₂+...+у_m)min

Егер (19) теңдіктерін сәйкес у₁, у₂,..., у_m-дер арқылы шешіп Х_j= 0 десек, онда у₁ =b₁>0,…, у_m=b_m>0 болар еді. Олай болса, у_i =b_i>0, Х _j= 0, шешуі (12) - (14) есептің шешуін береді, ал у_i =b_i>0, бұл есептің алғашқы базистік шешуі бола алады. Мұндағы у_i базистік белгісіздердің алғашқы есептің жасанды базисы деп атайды. Осы әрекеттерден кейін есепті шешуге симплекс әдісін қолдануға болады. Әрі қарай есепті шығару үшін мынадай жұмыстар жасалынады:

1. М -есебін қысқартылған немесе кеңейтілген кестеге жазады.

2. Симплекс кестенің бірінші жолына мақсат функцияның коэффициенттерін жазады. Егер мақсат функцияның босмүшесі болса, онда оны кері таңбамен бос мүшелер бағанасына жазу керек.

3. Бірінші бағанаға базистік белгісіздердің жолына солардың мақсат функциядағы коэффициенттері, ал базистік белгісіздердің белгілері екінші бағанаға жазылады.

4. Екінші жолға негізгі белгісіздердің (егер кеңейтілген симплекс кесте құрылса қосымша белгісіздердің де) белгілері жазылады.

5. Симплекс кестенің элементтері қарапайым симплекс әдісінің ережесі бойынша толтырылады.

6. Соңғы индекс жолының бағалары мына формула арқылы есептелінеді:

7. Оптималдық шартты тексеру. Шешім оптималды егер Z->max, онда ақырғы индекс жолдағы барлық негізгі белгісіздердің бағанасында жатқан элементтер оң сандар болса, ал кері жағдайда, яғни Z->min, онда осы элементтер теріс сандар болуға тиіс. Егер оптималды жағдай орындалмаса, екінші базисқа көшу үшін (келесі кестеге) жоғарыдағы түсіндірілген симплекс әдісі бойынша бағыттауыш бағанамен жолды анықтап, бас элементті табамыз. Алдымен индекстік жолдаң яғни L мақсат функцияның m + 2 жолы бойынша ең кіші мәнді (абсолюттік шамасы бойынша ең үлкен мәнді) іздейміз, яғни m + 2 жолдың элементтерінің теріс таңбаларының ішінде ең үлкенін табамыз.

Айталық, мұндай минималды ең кіші теріс сан k-ші бағанада жатсың ендеше бағыттаушы бағана ретінде k-ші бағананы алуға болады. Демек, Х_k-ші базистық емес белгісіз базис құрамына ену керек. Ал базис құрамынан шығайын деп отырған у-ты табу үшің барлық базистік белгісіздердің жолындағы бос мүшелер бағанасында тұрған элементтерді сол жолдарда бағыттаушы бағанада тұрған элементтерге бөлеміз де, ең кіші қатынасты анықтаймыз.

Осы қатынасқа сәйкес жолды бағыттаушы жол деп атаймыз. Оны r-мен белгілейміз. Демек, у_r - базис құрамынан шығады. Бағыттаушы жолмен бағыттаушы бағананың қиылысқан жерінде тұрған элемент бас элемент делінеді де, оны а_rk - деп белгілейді. Келесі кестені Х_k мен у_r орнын ауыстырып тұрғызамыз. Х_k мен у_r орындарын ауыстырғанда кестенің барлық коэффициенттері өзгереді.

Жаңа кестенің элементтері былай табылады:

- бас элементтің орнында тұратын элемент, егер кесте қысқартылған симплекс кесте түрінде құрылса:

ал егер кеңейтілген симплекс кесте түрінде құрылса, онда бұл элементтің орнына 1 жазылады, сонымен қатар бір аттас белгісіздердің қиылысында орналасқан торларға да 1 жазылады да, осы бағаналар нөлмен толтырылады.

- бағыттаушы жолдың орнында тұратын жаңа элементтер:

- бағыттаушы бағананың орнында тұратын жаңа элементтер:

- жаңа кестенің қалған элементтері

Бұдан кейін 7-пунктке көшеміз, яғни m+1 жолдың элементтерін тексереміз. Егер m+1 жолдың элементтері не оң сандар, не нөл болса, онда есеп шешілген.

Жоғарыдағы баяндалған алгоритмді мына мысалда қарастырайық.

Мысал. Мына шектеуші шарттарды қанағаттандыратын:

Төмендегі мақсат функцияның максималды мәнін анықтайық:

Z = 4Х₁ +2Х₂ + Х₃max

Канондық түрге өтейік

Бірінші және үшінші теңдеулерде базистік белгісіздер жоқ, сондықтан оларға жасанды базистік белгісіздер енгіземіз.

М-есебін алдық.

Әрі қарай есепті симплекс кестесін тұрғызу арқылы шығарамыз.

Кесте 5

Индекс жолындағы элементтерді есептеу:

Кестеден бағыттаушы бағана k=2және бағыттаушыжол r=2 таптық. Бас элемент a_rk = a₂₂= 2. Екінші симплекс кестені тұрғызайық.

Кесте 6

Екінші кестенің элементтері жоғарыдағы баяндалған алгоритм бойыша есептелінді. Есептің оптималды шешімі 4-ші симплекс кестеде табылды, яғни:

Кесте 7

Соңғы индекстік жолда барлық негізгі белгісіздердің бағанасында тұрған элементтер оң сандар және олар нөлге тең, яғни оптималды шартты алдық. Енді есептің шешімін векторлық түрде, базистік жолда тұрған белгісіздердің мәнін индекстерінің өсу тәртібі бойынша, бос мүшелер бағанасынан соларға сәйкес жолда тұрған сандарды мына тәртіпте жазамыз:

X(0;7;1;0;0;0;0); Z=15.

Сөйтіп, оптималдық жоспардан көріп отырмыз: Х₁= 0; Х₂= 7; Х₃= 1; Х₄= 0; Х₅= 0; У₁= 0; У₂= 0. Жасанды белгісіздердің мәндері (У₁=0; У₂= 0) нөлге тең болу себепті оларды оптималдық жоспардан алып тастап, негізгі есептің оптималды жоспарын былай көрсетуге болады:

X(0;7;1;0;0); Z=15.

Егер қойылған есептің шарты бойынша барлық шектеулер "кем емес", яғни (>=) түрде болатын болса, онда міндетті түрде мақсат функцияның минималды (Z —> min) мәні ізделінеді. Мұндай жағдайда есепті М - коэффициентінсіз шығаруға болады және есептеу әрекеттері біраз жеңілденеді.

СПЕ қосалқы есептері

Бастапқы СП есебі бойынша қосалқы есептің қалай анықталынатынын қарастырайық. Айталық, бастапқы есеп мақсат функцияның максималды мәнін іздейтін есеп болсын:

Z = С₁Х₁ + С₂X₂ +... + С_n X_n max (1)

мына жағдайда:

(2)

(3)

1-анықтама: Мақсат функцияның минималды мәнін іздейтін есеп: F=b₁y₁+b₂y₂+…+b_my_mmin (4)

мына жағдайда:

(5)

(6)

(1) - (3) есептің қосалқы есебі делінеді.

Жоғарыдағы келтірілген екі есепті салыстыра отырып, қосалқы есеп алғашқы есепке байланысты мынадай ереже бойынша құрылатынын байқауға болады:

1. Егер бастапқы есептің (1) - (3) мақсат функциясы максимумге ізделінсе, онда қосалқы есептің (4) - (6) мақсат функциясы минимумге ізденеді (немесе керісінше).

2. Қосалқы есептің матрицасы

(7)

бастапқы (1) - (3) есептің (2)-шектеулер жүйесінің белгісіздерінің коэффициенттерінен құралған, яғни мына матрицаға сәйкес:

(8)

және осы матрицаны транспарттау жасау арқылы анықталған.

3. Қосалқы есептегі (4) - (6) белгісіздердің саны бастапқы есептің (1)- (3) шектеулер жүйесіндегі (2) қатынастардың санына, ал қосалқы есептің (5) жүйесіндегі шектеулердің саны бастапқы есептегі (1) - (3) белгісіздердің санына тең.

4. Бастапқы есептің (2) жүйесіндегі шектеулердің бос мүшелері қосалқы есептің мақсат функциясы белгісіздерінің (4) коэффициенттері, ал қосалқы есептің (5) жүйесіндегі шектеулердің оң жағындағы бос мүшелер, бастапқы есептің мақсат функциясы белгісіздерінің коэффициенттерінен құралады.

5. Егер бастапқы есептің (1)-(3) Х_j-айнымалысы тек оң мәндерді қабылдайтын болса (X_j 0), онда қосалқы есептің (5) - жүйедегі j- шектеуі теңсіздік түрінде беріледі, ал егер X_j - айнымалы кез-келген мәнді қабылдайтын болса (0X0), онда j –шектеуі теңдеу түрінде беріледі. Осындай қатынас бастапқы есептің шектеулерімен (2) және қосалқы есептің айнымалылары арасында да сақталады. Егер (2) жүйедегі i-қатынас теңсіздік болса, онда қосалқы есептің у_i - айнымалысы тек оң мәнді, яғни у0. Керісінше жағдайда, яғни i-қатынас теңдік болса, онда у_i кез-келген мәңд қабылдай алады (0 у0).

Мысал: Мына СП есебінің қосалқы есебін құру керек.

Шешуі:

Қосалқы есептің айнымалылар саны бастапқы есептің жүйесіндегі теңдіктер санына тең, олай болса оларды: у₁ у₂ және у₃ деп қабылдайық. Мақсат функция белгісіздерінің коэффициенттері бастапқы есеп шектеулерінің оң жағындағы бос мүшерелеріне тең, олар: 12, 24,18.

Сонымең қосалқы есеп:

түрде жазылады.

Қосалқы есепті жазудың жалпылама ережесі

Жоғарыдағы келтірілген қосалқы есептің құру ережесін талдап, оның мынадай жалпылама жазылу ережесін тұжырымдайық:

1. Егер тура (бастапқы) есептеу j-айнымалыға теріс болмау шарты (X0) берілсе, онда осы айнымалыға сәйкес қосалқы есептің шектеуі теңсіздік (оның "" немесе "" жазылуы мақсат функцияның қандай мәні ізделуіне байланысты) болуы керек.

2. Егер тура есепте j-айнымалыға теріс болмау шарты берілмесе (0Х 0), онда осы айнымалыға сәйкес қосалқы есептің шектеуі тендік ("=") түрінде жазылады.

3. Егер тура есепте шектеу теңдік түрінде берілсе, онда қосалқы есептің осы шектеуге сәйкес айнымалысына теріс болмау шарты қойылмайды.

4. Егер тура есепте шектеулер теңсіздіктер түрінде ("" немесе "") берілсе, онда қосалқы есептің осы шектеулерге сәйкес айнымалыларына теріс болмау шарты қойылады.

Бастапқы СПЕ-ді "X" - есептері, қосалқы есептерді "У" - есептері деп атау келісілген.

Қосалқы жүп есептер симметриялы, симметриялы емес және аралас қосалқы есептер болып бөлінеді.

Дәріс 6. Тақырып: Тасымалдау есебі.

Тасымалдау есебі. Потенциалдар әдісі. СБ есепті шешудің тұрақтылығы. Тұрақтылықтың талдауы.

Транспорттық есептердің математикалық қойылуы

Транспорттық есеп - сызықты программалау есебінің тәжірибеде ең көп тарағандарының бірі. Оның негізгі мақсаты тауарларды тиімді және ұтымды тасымалдау жоспарын құру болса, тәжірибеде осы есептің математикалық аппараттарына және шығару алгоритмдеріне сәйкес келетін есептердің түрлері көптеп кездеседі. Сондықтан, мұндай есептер халық шаруашылығында маңызды есептердің қатарына жатады.

Транспорттық есептердің тәжірибелік маңызын терең ұғыну үшін қарапайым есептердің алғашқы қойылуын қарастырайық. Мысалға, айталық үш шаруашылықта өндірілген бидайды екі элеваторға тасу жоспарын құру керек. Бірінші шаруашылықтан 10 мың тонна, екінші шаруашылықтан 8 мың тонна, ал үшінші шаруашылықтан 7 мың тонна бидай тасылатын болсын. Бірінші элеватор 11 мың тонна, ал екінші элеватор 14 мың тонна бидайды қабылдай алсын. Есептің мақсаты, қандай шаруашылықтан қай элеваторға қанша бидай тасығанда тасуға кеткен жалпы шығын аз болатын жоспар құру.

Бұл жерде қатынас шығыны туралы мәселе көтеріліп отыр, шындығында, қатынас шығыны жол қашықтығына байланысты болмауы мүмкің ол: а) элеватор мен шаруашылық аралығына; б) жолдың техникалық жағдайына в) транспорттың түріне; г) транспорттың техникалық жағдайына, т.б. мәселелерге тәуелді болады. Демек, қатынас шығыны сызықты түрде өзгермейді. Сондықтан, 1 тонна бидайды әр шаруашылықтан әр элеваторға апарған шығынды белгілі деп есептейік және жалпы бұл көрсеткішті С_ij-деп белгілейік (мұндағы i- қабылдайтын орынның нөмірі немесе математикалық тілде индексі, j-жүкті жіберетін орынның нөмірі немесе индексі). Сонымен қатар бірінші шаруашылықты – Ш₁ екінші шаруашылықты - Ш₂, ал үшінші шаруашылықты -Ш₃ және бірінші элеваторды – Э₁, екінші элеваторды - Э₂ деп белгілеп, оларға сәйкес бір тонна бидайды әр шаруашылықтан, әрбір элеваторға тасуға кететін шығынды мына кестеге өзіне сәйкес торға жазайық.

Мұндағы С₁₁= 8 теңге дегеніміз 1 -элеваторға 1 -шаруашылықтан 1 тонна бидайды тасуға кететін шығын, ал С₁₂=6 теңге 1 -элеваторға 2-шаруашылықтан 1 тонна бидай тасуға кететін шығың тағы сол сияқты, соңғы С₂₃= 7 теңге 2-элеваторға 3-шаруашылықтан бір тонна бидайды тасуға қажетті шығын (бұл жерде сан мәндері есептің шартын түсіну үшін жуықтап алынған).

Енді осы есептің математикалық моделін құрайық. Ол үшін 1-элеваторға 1-шаруашылықтан таситын бидай көлемін Х₁₁ деп, 1-элеваторға 2-шаруашылықтан таситын бидай көлемін Х₁₂ деп, тағы сол сияқты және соңғы 2-элеваторға 3-шаруашылықтан тасылатын бидай көлемін Х₂₃ деп белгілесек, мақсат функция былай жазылады:

Шектеу шарттары:

а) барлық шарушылықтардан тасымалдауға арналған бидай көлемдері толығымен тиісті орындарына жеткізіледі, олай болса:

б) бидай әр элеваторға керекті мөлшерде тасылуы керек

в) тасымалдауға арналған бидай көлемі теріс сан болуы мүмкін емес:

X₁₁0, X₁₂0, X₁₃0, X₂₁0, X₂₂0, X₂₃0,

Жоғарыда көрсетілген қарапайым мысалды негізге ала отырып, қатынас есептерінің жалпы математикалық моделін жазу үшін төмендегідей шартты белгілерді және атауларды қабылдайық.

Жалпы бір тектес өндірілген (шығарылған) өнімді бір тектес жүк, өнім өндіретін орындарды жүк жіберетін пункттер, ал өнім қабылдайтын орындарды тұтынушы пункттер деп атайық. Негізінде мұндай атаулар жуықтап шартты түрде есептің қойылу мағынасы түсінікті болу үшін қабылданған, себебі тәжірибеде халық шаруашылығында, оның ішінде ауыл шаруашылығында транспорттық есепке ұқсайтын есептер көптеп кездеседі.

Айталық, жүк жіберетін пункттердің саны - m (олардың нөмірлерін j - десек, онда j=1,2,...,m), ал тұтынушылардың саны - n (олардың нөмірлерін i-десек, онда i=1,2,... n) деп белгілейік. Әр жүк жіберетін пункттерді нөмірлеріне сәйкес (А₁, А₂,...А_m), ал тұтынушыларды нөмірлеріне сәйкес (В₁, В₂,...В_n) деп атайық. Жүк жіберетін пункттерде өндірілген (а₁, а₂, ...а_m) және тұтынушыларға керекті (b₁ b₂, ...b_n) жүк көлемдері делік.

С_ij-i-ші тұтынушыға j-ші жүк жіберетін пункттен жүкті тасығанда, оның бір өлшем бірлігіне шаққандағы шығын (мұндағы i=1,2,.n; j=1,2,...m), яғни С₁₁ С₁₂, ...С_nm. Бұл көрсеткіш әр түрлі мағынада болуы мүмкін: шығын, уақыт, еңбек өнімділігі және т.б.с.с. Әдебиеттерде бұл көрсеткішті тасымалдаудың "Тарифы" немесе кестеге жазылғаннан кейін i-ші жолмен j-ші бағананың қиылысында тұрған тордың бағасы деп атайды.

Кесте 1

X_ij - i-ші тұтынушыға j-ші жүк жіберетін пункттен таситын жүктің оптималды мөлшері, яғни таситын жүк көлемі белгісіз (Х₁₁, Х₁₂, .-.Х_nm). Тұрғызылатын математикалық моделдің мағынасы түсінікті болу үшін көмекші кесте құрайық (1-кесте).

Есептің мақсаты әр жүк жіберетін пункттен барлық тұтынушыларға тиісті мөлшерде жүкті аз шығынмен тасымалдау жоспарын құру, олай болса барлық шығын:

Z = С₁₁X₁₁ + С₁₂Х₁₂+...+ С_nmХ_nm→min (1)

Мына жағдайда:

а) барлық жүк жіберетін пункттерден тасымалдауға арналған жүк көлемдері толығымен тиісті орындарына жеткізілінеді, олай болса:

(2)

б) жүк әр тұтынушыға керекті мөлшерде тасылуы керек

(3)

в) әр жүк жіберетін пункттен әр тұтынушыға таситын жүктің мелшері теріс сан болуы мүмкін емес (яғни Х_ij> 0 - жүк тасу тиімді немесе Х_ij=0 -жүк тасу тиімсіз):

Х₁₁0, Х₁₂0 Х_nm0. (4)

Сонымен (1) - (4) жалпы транспорттық есептің кеңейтілген моделі болып есептелінеді.

_j- - қосынды белгісі арқылы транспорттық есептің математикалық моделін құрама түрінде керсетейік:

Шектеу шарттары:

Мына жағдайда:

яғни барлық жүк жіберілетін пункттерде өндірілген немесе жиналған жүктің көлемі толығымен тұтынушылардың сұраныстарын қамтамасыздандырады. Мұндай транспорттық есеп жабық деп саналады.

Егер математикалық модельде

шарты орындалмаса, мұндай транспорттық (қатынас) есептерінің моделін ашық модель деп атайды.

Транспорттық есептің моделі ашық болған жағдайда есепті шешу үшін оны жабық транспорттық есепке айналдырады.

болса, онда жүк артық өндірілген, мұндай жағдайда есепті жабу үшін жалған тұтынушы (В_n+1) енгізіледі де, оның жүкке сұраныс мөлшерін мына қатынаспен есептейді: b_n+1=a_j-b_i

болса, онда өндірілген өнім мөлшері тұтынушылардың сұраныс мөлшерін толығымен қамтамасыз етпейді, мұндай жағдайда есепті жабу үшін жалған жүк жіберуші пункт (А_m+1) енгізіледі де, ондағы жиналған жүк мөлшерін мына қатынаспен есептейді. a_m+1=b_i-а_i

Жүктің бір бірлігін тасуға кететін шығын (жалған тордың бағасы), яғни бірінші жағдайда С_n+1,₁= 0, С_n+1,2= 0,...,С_n+1,m= 0, ал екінші жағдайда С₁,_m+1= 0, С _2,n+1= 0,...,С_n,m+1= 0 деп алынады.

Баяндалып отырған тақырыпты қорыта келе жоғарыдағы келтірілген транспорттық (қатынас) есептің математикалық моделі халық шаруашылығының кептеген есептерінің математикалық аппараттары негізін құрайтынын атап етейік. Мысалға, ауыл шаруашылығында ауыспалы егістік жерлерді тиімді жоспарлауда, техниканы әртүрлі жұмысқа тиімді белуде, ендіріс мамандарын әртүрлі жұмысқа тиімді бекітуде, ендіріс орындарын тиімді түрде орналастыруда, тағы басқа да кептеген есептерде қолданылады.

Транспорттық есептерді шешу алгоритмдері

Жалпы алғанда қатынас (транспорттық) есебі сызықты програм-малау есебінің құрамына енеді. Жоғарыда қарастырылған сызықты программалау есептерінің математикалық моделінде белгісіз Х-тер тек бір ғана индекспен j=1...n берілген. Ал қатынас (транспорттың) есебінде белгісіздер екі индекспен анықталады.

Транспорттық (қатынас) есебін симплекс әдісімен шығаруға болады. Ол үшін екі индексті (өлшемді) көрсеткіштер бір индексті керсеткіштерге ауыстырылады.

Мысалы: Х₁₁⁼ У₁, Х₁₂= У₂, Х₁₃= У₃, Х₁₄= У₄, Х₂₁= У₅, Х₂₂= У₆, жәнв т.б.с.с.

С₁₁= В_1, С₁₂= В₂, С₁₃= В₃, С₁₄= В₄, С₂₁= В₅, С₂₂= B₆, және т.б.с.с.

Осы әрекеттердің нәтижесінде қатынас есебінің математикалық моделі жоғарыдағы баяндалған сызықты программалау есебінің симплекс әдісімен шығарылатын түріне ауысады. Сөйтіп, есепті шығару үшін симплекс әдісін қолдануға болады.

Дегенменде, есептің шарты қарапайым, ал ізделінетін белгісіздер өте көп және есепті ешқандай есептеу техникасыз қолмен симплекс әдісін қолданып шығару өте ыңғайсыз.

Осы келтірілген жағдайларға байланысты ғалымдар транспорттық есепті шығарудың симплекс әдісінен басқа жолын қарастырды. Қазіргі кезде транспорттық есептерді шығаруға өте көптеген әдістер жасалынған: үлестіру (тарату) әдісі, Венгер әдісі, потенциал әдісі, Вогель (Фогель) әдісі және тағы басқа да әдістер. Солардың ішінен 1949 жылы Кеңестер Одағының белгілі математигі академик Л. В. Канторович және М. К. Гавурин ұсынған тарату (үлестіру) әдісі тәжірибеде кеңінен қолданылады.

Транспорттық есептерді шешуге арналған әдістердің көпшілігі осы есептердің математикалық моделінің мына қасиеттеріне сүйенеді:

• барлық шектеуші шарттар тек теңдік түрінде беріледі;

• әрбір белгісіз тек екі-ақ теңдеудің құрамына енеді;

• шектеуші шарттардағы белгісіздердің коэффициенттері бірге тең.

Транспорттық есептерді шешуге арналған барлық әдістерді қолданғанда есепті кесте түрінде жазып шығарады. Әрқашанда есепті шешу тірек жоспарын құрудан басталады (кейде мұндай жағдайды базистік шешім деп те атайды). Математикалық программалау пәніне арналған әдебиеттерде тірек жоспарын құрудың бірнеше тәсілдерін кездестіруге болады. Солардың ішінде ең көп кездесетіндері:

• солтүстік-батыс бұрышы ережесі;

• екі есе ұтымды ережесі;

• жол немесе бағана бойынша ең кіші элемент ережесі;

• кестедегі матрицалардың ең кішісі ережесі;

• Вогель (Фогель) әдісі.

Осы ережелердің бірімен тірек жоспарын құрғанда әрқашанда толтырылған торлардың саны мына талапқа дәл болуға тиіс: К_m=m+n-1, бұл жағдай үлестіру әдісінің бірінші талабы.

Үлестіру (тарату) әдісі

Үлестіру (тарату) әдісі транспорт есебін шешуге арналған ең бірінші және тірекжоспарын біртіндеп жақсартуды схема түрінде нақтылы көрсетіп бейнелейтін әдіс. Ол осы әдістің негізінде жасалынған МОДИ әдісін (модификацияланған тарату) оқып үйренуге жақсы кіріспе болып табылады.

Үлестіру (тарату) әдісінің алгоритмі

1. Жоғарыда көрсетілген ережелердің бірімен тірек жоспары құрылады.

2. Барлық бос торлар үшін цикл тұрғызылады.

Цикл тұрғызу тәртіптері:

а) цикл бос тордан басталады және осы торда аяқталады;

б) циклда 1-тор ғана бос (толтырылмаған), ал қалғандары базистер (толтырылған) болады;

в) цикл сызықтары кестенің тік жолымен және бағаналарымен ғана өте алады. Диагональ бойынша өтуге болмайды;

г) 1-бос тордан басқа циклдың бұрылу бұрышында тұрған торлар міндетті түрде базистік болады.

3 Бос торлардың сипаттамалары мына формуламен есептелінеді

мұндағы С_ij^Т - циклдың тақ торларының бағалары; С_ij^ж - циклдың жұп торларының бағалары.

4. Оптималды жағдайдың белгісін тексеру. Егер Z —> mіn, онда барлық бос торлардың сипаттамасы оң сан болса, яғни: Δ_ij 0, базистік шешім оптималды делінеді.

Егер Z —> mах, онда барлық бос торлардың сипаттамасы теріс сан болса, яғни: Δ_ij <0, базистік шешім оптималды делінеді.

Ескерту: Егер құрылған жоспар оптималды емес және бірнеше теріс сипаттама болса, онда осы сипаттамалардың ең кішісі бойынша цикл құрылады да, турлендіру жүргізіледі, яғни бір рет орнын ауыстыру әрекеті жасалынады.

Түрлендіру тәртібі және бір рет ауыстыру

а) бос тордан бастап циклдың бұрыштарына (төбелеріне) оң және теріс (+, -) таңба жазылады. Циклдің бос торы әрқашанда бірінші (ол тақ). Циклдың тақ төбелеріне"+", ал жұп төбелеріне"-" таңбалары жазылады.

б) теріс таңбалы торлардың ішінен ең кіші элемент жазылған тор ізделінеді, яғни:

λ = min{X_ij}

в) оң таңбалы торларда тұрған элементтерге осы табылған ең кіші элемент қосылады да, ал ол теріс таңбалы торларда тұрған элементтерден алынып тасталынады.

Ескерту. Егер циклдың жұп төбелерінде шамалары бірдей ең кіші (λ_min ) базистік айнымалылар болса, онда мақсат функциясына қарағанда бағасы ең төмен (яғни бағасы мақсат функцияны жақсартпайтын) тор бос (толтырылмаған) деп есептелінеді де, ал қалған шамалары бірдей минималды элементтері бар торларда базистік айнымалылар нөлге тең делінеді.

Мысал. Бидайды 30 га, қарабидайды 20 га және сұлыны 20 га егу жоспарланған. Ауыспалы егістік жер үш бөлімнен тұрады: 25, 35 және 10 га.

Әр бөлімнен алынатын өнім белгілі, ол мына кестеде көрсетілген:

Ауыспалы егістік жер бөлімдеріне, максималды өнім алуды қамтамасыздандыратын дақылдарды егу жоспарын құру керек.

Шешімі. Алғашқы тірекжоспарың "солтүстік-батыс бұрышы" ережесімен құрайық.

"Солтүстік-батыс бұрышы" ережесінің алгоритмі

Есептің шарты бойынша бірінші үлестіріп тарату кестені "солтүстік-батыс бұрыш" ережесін қолданып тұрғызайық:

а) үлестіру кестесін түрлендіру, оның ең жоғарғы сол жақ бұрышындағы торды толтырудан басталады. b_i- қорлар және а_j- сұраныстар салыстырылады (алғашқы қадамда i = 1 және j = 1);

б) егер b_i>а_j, онда осы торға X_ij=b_i-ді жазады. Торды базистік деп атайды. Жаңа қор мөлшері есептелінеді: b_i^ж=b_i -a_j , j- бағана кестеден ойша алынып тасталынады. Әрі қарай а) пунктіне j - бағанасы алынып тасталынған жаңа кестеге өтеміз;

в) егер b_i < а_j, онда осы торға Х_ij =b_j ді жазады. Торды базистік деп атайды. Жаңа сұраныс мөлшері есептелінеді: a_j^ж=a_j-b_{i ,} i-жол кестеден ойша алынып тасталынады. Әрі қарай а) пунктіне i-жолы алынып тасталынған жаңа кестеге өтеміз;

г) мынадай: b_i=а_j-жағдай болуы мүмкін. Мұндай жағдайда қарастырылып отырған тор толтырылады да, бағана және жол кестеден ойша алынып тасталынады. Мысалға, торға Х_ij=b_i-ді жазсақ, жаңа сұраныс a_j^ж=0, i-жол кестеден ойша алынып тасталынады.Әрі қарай а)пунктіне i-жолы алынып тасталынған жаңа кестеге өтеміз;

д) кестенің ақырғы торын толтырғанда қалған сұраныстыңда және қордыңда шамалары бірдей болады, сөйтіп ақырғы жол мен бағанада кестеден ойша алынып тасталынады.

Осы баяндалған алгоритм бойынша қарастырылып отырған есептің алғашқы тірек жоспары үлестіру кесте түрінде тұрғызылды (2-кестені қараңыз).

Толтырылған торлар санын есептейік:

К_m=m +n-1 =3 + 3-1=5.

Тірек жоспарында да 5 тор толтырылған (кестені қараңыз).

Кесте 2

Әрбір бос торлар үшін цикл құрамыз:

Ескерту: Цикл төбелерінде жақша ішінде торлардың бағалары, ал жақшасыз онда жазылған сандар. БТ-бос торлар және олардың адрестері. Бос торлардың сипаттамаларын мына формуламен есептейік:

Бір тор ғана [1,3] оң сипаттамалы, сондықтан базистік шешім оптималды емес. Осы тор бойынша түрлендіру, яғни бір рет орнын ауыстыру әрекетін жүргізейік.

Тағы да әр бос тор үшін цикл құрамыз да сипаттамаларын есептейміз

Барлық Δ_ij<0, сондықтан базистік шешім (жоспар) оптималды, яғни ауыспалы егістің 1-бөлімінен 25 га және 3- бөлімінен 5 га жерге бидай, 2-бөлімнің 20 га жеріне қарабидай, сонымен қатар, оның 15 га және 3-бөлімнің 5 га жеріне сұлы егілсе, шаруашылық дәнді дақылдардан максималды өнім алады. Бұл өнімнің шамасы: Z=13*25+ 12*5 +18 *20+15*15+17*5 =1075 өлшемдей болуға тиіс.

Есептің шешімі математикалық тілде былай жазылады:

Кесте 3

МОДИ әдісі (потенциалдар әдісі) және оның алгоритмдері

Үлкен өлшемді кестелерде транспорттық есептерді үлестіру (тарату) әдісімен шығарғанда, циклдер құрып сипаттамаларды есептеу, есептің ең ыңғайсыз ауыр кезеңі болып есептелінеді. Осындай есептерді модификацияланған тарату әдісімен (МОДИ) шығарғанда есептеу технологиясы көп жеңілденеді. Цикл құрмай-ақ бос торлардың сипаттамаларын мынадай формуламен есептеуге болады:

Δ_ij=C_ij-(U_i+V_j), (5)

мұндағы C_ij- бос торлардың бағасы; U_i - кестенің i-жолының потенциалы; V_j - кестенің j-бағанасының потенциалы.

Негізінде МОДИ әдісі үлестіру (тарату) әдісімен сәйкес, ал потенциалдар әдісінен айырмашылығы бос тордың сипаттамасын анықтайтын формуланың таңбасы әртүрлі.

Ескерту: Потенциал деп мына формуламен: С_ij^m=U_i+V_j есептелген кез келген сандар жүйелерін айтады. Мұндағы С_ij^m - толтырылған (базистік) тордың бағасы; U_i сияқты α_i- кестенің i- жолының потенциалы; V_j сияқты β_j – кестенің j -бағанасының потенциалы.

МОДИ алгоритмі

1. Алғашқы тіректік шешім жоғарыдағы айтылған ережелердің бірімен құрылады.

2. Базистік (толтырылған) торларға мына формула бойынша:

С_ij^m=U_i+V_j (6)

толтырылған тордың жолының - U_i және бағанасының - V_j потенциалдарын анықтаймыз.

Ескерту: 1-ші - жолдың потенциалын U_i = 0 деп алған жөн.

3. Бос (толтырылмаған) торлардың сипаттамаларын мына формуламен есептейміз: Δ_ij=C_ij-(U_i+V_j).

4. Келесі жасалатын әрекеттер үлестіру (тарату) әдісімен бірдей.

Осы баяндалған әрекеттерді жай бір қарапайым мысал арқылы есептің тәжірибелік мән жайына тоқталмай-ақ талқылайық.

Мысал. Мына мақсат функцияның ең кіші мәнін беретін L=3Х₁₁₊ 6Х₁₂+ 5Х₁₃+ Х₁₄+ X₂₁ +4Х₂₂+3Х₂₃+2Х₂₄+4Х₃₁+ 3Хз₂+ Х₃₃+2X ₃₄ және төмендегі шектеуші шарттарды:

Қанағаттандыратын Х_ij-лердің(i=1,2, 3; j= 1,2,3;4) мәнін табу керек. Есептің берілген шартын кесте түрінде көрсетейік (4-кесте). Сонымең транспорттық есептерді шешу жолы негізінен үш кезеңнен тұрады:

а) алғашқы тірек жоспарын құру, яғни базистік шешімді табу;

б) табылған шешімді оптималдық жағдайға тексеру;

в) егер табылған шешім оптималды болмаса, онда жаңа базистік шешімге көшеміз, бұл әрекет оптималды шешім табылғанша жүргізіле беріледі.

кесте 4

1-кезең. Берілген есеп үшін алғашқы тірек жоспарын құрайық (5-кесте).

Алғашқы базистік шешімді табамыз, яғни жоғарыдағы келтірілген ережелердің бірімен торларды толтырамыз.

Кесте 5

Қабылданған ереже бойынша толтырылуға тиісті торды анықтағаннан кейін оның жолындағы және бағанасындағы элементтерді бір-бірімен салыстырып, ең кішісін сол торға жазады.

Айталық тірек жоспарын құру үшін "солтүстік-батыс бұрышы" ережесі қабылдансын.

Элементтерді толтыру тәртібі: ең алдымен 1-ші торды толтырамыз, ол үшін min {b_i,а_i,} табамыз, min{100,300} = 100, демек Х₁₁ =100. Бұл табылған мәнді (В₁,A₁) 1-ші торға жазамыз. Сонымең В₁ тұтынушының сұранысы орындалды, олай болса енді бұл жолға сан жазуға болмайды. Ереже бойынша диагональ бойымен қозғалу тәртібін сақтай отырып, келесі жолға көшеміз де (В₂,А₁) торына жазылатын Х₂₁-дің мәнін табамыз, ол:

Х₂ = min{400,300 – Х₁₁} = min{400,200}=200

Х₁₁+ Х₂₁= 300 тең болды, демек А₁-ші пункттен жүк толығымен тасылып бітті. Бұдан кейін әлі қарастырылмаған (В₂, А₂) торға өтеміз де Х₂₂-нің мәнін табамыз:

Х₂₂= min{b₂ - х₂₁, а₂} = min{400 - 200, 500}=200.

Табылған X₂₂ = 200 мәнді (В₂,A₂) торына жазамыз, ал Х₂₁+Х₂₂= 400-ге тең, демек В₂-ші тұтынушының жүкке сұранысы толық орындалды. В₃-ші тұтынушыға, яғни 3-жолға көшеміз де Х₃₂-мәнін табамыз:

Х₃₂= min{b₃, а₂ - х₂₂}= min{600, 500 - 200}=300.

Табылған Х₃₂=300 мәнді (В₃, А₂) торына жазамыз, ал Х₂₂+Х₃₂=500, демек А₂-пункттен жүк толығымен тасылып бітті. Олай болса, А₃-пунктке (В₃,А₃) торына көшеміз де Х₃₃-мәнін табамыз:

Х₃₃= min{b₃ - х₂₂, а₃} = min{600 - 300, 100} = 100.

Табылған Х₃₃= 100 мәнін (В₃,А₃) торына жазсақ А₃-пункттен жүкті толық тасығанымыз байқалады. Енді А₄-пунктке өтеміз (В₃,А₄) де Х₃₄-мәнін табамыз:

Х₃₄= min{b₃ - х₃₂- х₃₃, а₄} = min{600 - 300 -100, 200} = 200.

Бұл мәнді (В₃, А₄) торына жазсақ, А₄-пункттен де жүкті тасымалдап біткенімізді байқадық, Сонымен, барлық пункттен жүктерді толығымен тасып болдық, ал тұтынушылардың жүкке сұраныстары толығымен қамтамасызданды, демек тірек жоспар құрылып бітті. Толтырылған торлардың саны: K_m=4+3-1=6, қойылған талаппен бірдей.

Элементтер (сандар) жазылған торларды базистік торлар деп, ал қалған торларды толтырылмаған бос торлар деп аталатыны жоғарыда айтылды. Бос торларда тұрған Х_ij=0, бұларды бос белгісіздер дейміз. Табылған жоспар:

Х₁₁ = 100, Х₁₂= 0, Х₁₃= 0, Х₁₄= 0, Х₂₁= 200, Х₂₂= 200,

Х₂₃= 0, Х₂₄= 0, Х₃₁= 0, Х₃₂= 300, Х₃₃=100, Х₃₄= 200.

Бұл жоспарды іске асырғанда, кететін қатынас шығынын табу үшін мақсат функцияның (Z) мәнін есептейік:

Z= 100*3 + 200*1 + 200*4 + 300*3 +100*1 + 200*2 = 2700 ақша өлшем бірлігі. Сонымен есепті шешудің 1-ші кезеңі бітті. 2-кезең. Базистік шешімнің оптималдығын тексеру.

Симплекс әдісі сияқты бұл жағдайда да табылған базистік шешім және мақсат функция базистік емес бос белгісіздер арқылы өрнектеледі. Бірақ бұл жағдайда бос белгісіздердің коэффициенттері С_ij болмай, басқа мәнге өзгеріп кетеді. Ал сол өзгерген С_ij -лердің (бос белгісіздердің) орнында тұратын коэффициенттерді Z_ij- деп белгілесе, онда мақсат функция бос белгісіздер арқылы былай жазылады:

Z = Z₁₊ d₁₂Х₁₂+ d₁₃Х₁₃+d₁₄Х₁₄+ d₂₃Х₂₃+ d₂₄Х₂₄+ d ₃₁X₃₁ (7)

мұндағы Х_1j - базисқа енбеген бос белгісіздер (базистік белгісіздерге енген белгісіздер арқылы Z₁-ді таптық). Егер (6.7) формулада d_ij-лердің ішінде теріс таңбалары болса, онда (7) теңдеуі бойынша (d_ij< 0, Х_ij< 0, онда d_ijX_1j< 0) Z -дің мәнін азайтуға болады:

Z₂ = Z₁ -d_kbX_kb, демек Z₂<Z₁

Бұл жағдайда табылған шешімді жақсартады. Ал егер d_ij > 0 болса, онда шешімді әрі қарай жақсарта алмаймыз, өйткені Z₂ = Z₁ +d_kbX_kb, Z₂> Z₁ Бірақ бұл идеяны әрбір бос белгісіздер арқылы іске асыру (d_ij-лердің мәнін тауып таңбасын тексеру) үшін көп есептеулер жүргізу kерек. Сондықтан, бұл идея басқа жолмен іске асырылды. Ол үшін әрбір бос тордың базиске ену мүмкіндігі бар ма, жоқ па? Егер бір базистік тор басқа базистік емес тормен орнын ауыстырса, жоспар (мақсат функция) жақсара ма әлде жоқ па? - деген заңды сұрақтар туылады. Бұл сұрақтарға жауап беру үшін әр жолға сәйкес U_i, ал әр тік бағанаға сәйкес V_j коэффициенттерін қабылдайық. Олардың қалай аталатынын жоғарыда баяндадық. Осы коэффициенттер арқылы бос торлардың барлығына сипаттама беріледі. Ал U_i және V_j коэффициенттері толтырылған торлармен мынадай қатынаста болатыны жоғарыда айтылды:

U_i +V_j = С_ij^Т. (8)

Толтырылған торлар үшін (6.8) теңдеуі орындалатыны түсінікті, ал бос торлар үшін (8) теңдеуі орындалмайды. Олай болса бұл айырмашылықты, яғни d_ij-ді былай қарастыруға болады:

d_ij =С_ij-U_i-V_{j (9)}

Демек, (9) бойынша оптималдық жағдай тексеріледі, яғни егер барлық бос торлар үшін d_ij>0 болса, онда табылған шешім оптималды шешім делінеді, d_1j< 0 болса, онда жоспарды жақсарту керек.

Көп жағдайларда теріс таңбалы болатын d_ij-лер біреу емес, бірнешеу болуы мүмкін. Мұндай жағдайларда max{|d_ij|}=d_ij ішінен ең кішісіне d_ij<0 сәйкес бос торды табамыз да, соған байланысты алғашқы жоспарды қайта қарастырып, одан тиімді басқа шешімді аламыз, яғни 3-ші кезеңге көшеміз

3-ші кезеңге көшудің алдында берілген есеп үшін d_ij-лерді есептейміз. (8) теңдеуі бойынша тірек жоспар құрылған кестесінің жолдарының және бағаналарының потенциалдарын анықтаймыз. Ол үшін толтырылған тор үшін (8) теңдеуі жазылады да не U_i -ге, немесе V_j -ге кез келген бір мән беріледі. Көп жағдайда біреуін нөлге теңейді. Мысалы, есепте(В_1, А₁) торы толтырылғаң ендеше осы тор үшін (8) теңдеуін жазып U_i және V_j -ді табалық:

С₁₁=U₁+V₁

Егер мұндағы U₁=0 десек, онда С₁₁= 0+V₁, немесе 3=0+V₁, V₁= 3. Осы формуламен есептелініп табылған потенциалдардың мәні 6-кестеде көрсетілген.

Кесте 6

Табылған V₁, арқылы базистік тор (В_2,A₁) үшін U₂-ні есептейік:

U₂+V₁ =С_{21 ,} U₂ +3=1, U₂ =-2.

(В₂,А₂) базистік тор үшін:

U₂+V₂=С_{22 ,} -2+V₂=4, V₂=6.

Сол сияқты базистік тор (В₃,А₂) үшін:

V₂ +U₃=С_{32 ,} 6+U₃ =3, U₃ =-3.

Базистік тор (В₃, А₃) үшін:

U₃+V₃=С_{33 ,} -3+V₃=1, V₃=4.

Ақырында (В₃,А₄) базистік тор үшін:

U₃+V₄=С_{34 ,} -3+V₄=2, V₄=5.

Осы табылған U_i және V_j коэффициенттерін пайдаланып, бос торлар үшін d_ij -ді есептеп таңбаларын тексереміз.

Табылған 7-кестеден алғашқы тірек жоспарының оптималды емес екені белгілі болды, өйткені (d₁₄=-4, d₂₄=-1) теріс сандар. Бірінші кезекте абсолюттік шамасы ең үлкен таңбасы теріс

айырымға сәйкес торды толтырамыз. Бұл (В₁, А₄) торына сәйкес келеді, демек ең алдымен осы торды толтырамыз. Осы шешімнен кейін үшінші кезеңге өтеміз

кесте 7

3-кезең. Жаңа базистік шешімді тұрғызу.

Бос торлардың сипаттамасының d_ij теріс таңбалы болуы мынаны көрсетеді:

а) табылған базистік жоспар оптималды жоспарды бермейді, демек оны жақсарту керек;

б) егер басқа толтырылған базистік торлардан теріс таңбалы бос торларға жүктер ауыстырылса, онда бір өлшем жүкті тасуға кететін шығын (d_ij <0) d_ij -дің мәніне кемиді де жоспар жақсарады.

Осындай жақсартылған тірек жоспарын құру үшін арнайы тәсілдер қолданылады. Солардың бірі "Тұйық бағытты айналыс" тәсілі. Осы тәсілді қолдану, таңдап алынған теріс таңбалы бос тор үшін тұйық бағытты айналыс контурын тұрғызудан басталады. Контур құру тәртібі "Үлестіру (тарату) әдісіне" негізделген.

Тұйық контурды тұрғызу тәртіптері:

а) тұйық контур бос тордан басталады да және осы торда аяқталады;

б) тұйық контурда 1 тор ғана бос (толтырылмаған), ал қалғандары базистер (толтырылған) болады;

в) тұйық контурдың сызықтары кестенің тік жолымен және бағаналарымен ғана өте алады. Диагональ бойымен өтуге болмайды;

г) 1 бос тордан басқа тұйық контурдың бұрылу бұрышында тұрған торлар міндетті түрде базистік болады.

Тұйық контурдың конфигурациясы (дене құрылысы) әртүрлі болуы мүмкін: квадратты, бір сатылы, көп сатылы, тік бұрышты тертбұрыш, бір немесе бірнеше рет қиылысқан және т.б.

Түрлендіру тәртібі және бір рет ауыстыру

а) бос тордан бастап тұйық контурдың бұрыштарына (төбелеріне) оң ("+") және теріс ("-") таңба жазылады. Тұйық контурдың бос торы әрқашанда бірінші (ол тақ). Тұйық контурдың тақ төбелеріне"+", ал жұп төбелеріне"-" таңбалары жазылады.

б) теріс таңбалы торлардың ішінен ең кіші элемент жазылған тор ізделінеді, яғни: λ= min{Х_ij};

в) оң таңбалы торларда тұрған элементтерге осы табылған ең кіші элемент қосылады да, ал ол теріс таңбалы торларда тұрған элементтерден алынып тасталынады.

Ескерту. Егер тұйық контурдың жұп төбелерінде шамалары бірдей ең кіші (λ) базистік айнымалылар болса, онда мақсат функциясына қарағанда бағасы ең төмен (яғни бағасы мақсат функцияны жақсартпайтын) тор бос (толтырылмаған) деп есептелінеді де, ал қалған шамалары бірдей минималды элементтері бар торларда базистік айнымалылар нөлге тең делінеді.

Қарастырылып отырған есепте d_ij< 0 болатын бос торлар саны екеу, олар: (В₁, А₄) және (В₂, А₄), ал жоғарыда айтылған бойынша бұлардың ішіндегі mах d_ij< 0 {d_ij}-ді алсақ, онда жүкті тасымалдауға кететін шығын көбірек азаяды. Осы тұрғыдан тірек жоспарды жақсартуды, яғни тұйық айналыс контурын құруды (В₁ А₄) торынан бастайық.

Тұрғызылған контурдың (В₁, А₄) келесі тебесіне оң ("+") таңбасын жазамыз да, контурдың бағыты бойынша келесі төбеге теріс ("-") таң-басын әріқарай кезекпен оң, терістаңбаларын ауыстырыпжазып шыға-мыз. Түрлендіру тәртібі бойынша теріс таңбалы торлардың ішінен ең кіші элемент жазылған тор ізделінеді, яғни:

Оң таңбалы торларда тұрған элементтерге осы табылған ең кіші элемент (100 шама) қосылады да, ал ол теріс таңбалы торларда тұрған элементтерден алынып тасталынады. Нәтижесінде жаңа базистік шешімі алынған кесте (8-кесте) тұрғызылады.

Сонымен жаңа жоспар (жаңа базис):

болып шықты. Бұл шешім базистік шешу бола алады, өйткені барлық талап орындалады:

кесте 8

а) барлық х > 0;

б) жол және бағана бойынша баланс сақталған: (толтырылған торлар саны да);

в) базистік белгісіздердің саны m+n-1 =4 + 3-1 =6 тең

г) барлық базистік X_ij бос Х-тер арқылы өрнектеліп отыр (кесте бойынша).

Базистік шешудегі мақсат - функция Z₂-нің мәнін тауып, алғашқы Z₁-дің мәнімен салыстыралық:

Z₂= 1*100+1*300+4*100+3*400+1*100+2*100 = 2300

Z₂<Z₁, яғни (2300 < 2700).

Сөйтіп, екінші жоспар бойынша тасу шығынын 400 теңгеге азайттық. (Шынында да - d_ijХ_ij =-400).

Ескерте кететін бір жай - әрбір бос тор үшін тек бір ғана контур құруға болады.

Жоспардың оптималдығын тексерейік. Ол үшін (6.8) формуланы қолданып, потенциалдардың мәнін анықтайық. Бірінші жолда толтырылған тор үшін: V₄+U₁=C₁₄. Бірінші жолдың потенциалы U₁=1 деп шешім қабылдайық (бұл жерде алғашқы потенциалдың мәніне кез кел-ген санды қабылдауға болатындығын тағы да ескере кетейік. Есептеу жұмыстарын жеңілдету үшін U₁=1 тең деп алдық). Олай болса\/₄+1=1, V₄= 0. Табылған V₄- пайдаланып U₃-ті табайық (В₃,А₄):

U₃ +V₄=C_34, U₃ =2-0=2.

Енді U₃-ті пайдаланып \/₃-ті табайық (В₃,А₃):

U₃ +V₃=C_33, 2+V₃=1, V₃=-1.

(В₃,А₂) торының бағасы С₃₂= 3 және U₃ = 2 арқылы V ₂- табамыз:

U₃ +V₂=C_32, 2+V₂=3, V₂=1.

Кесте 9

(В₂, А₂) торы бойынша U₂-ті табамыз:

U₂ +V₂=C_22, U₂+1=4, U₂=3

Ақырғы (В_2, A₁) торының бағасы С₂₁ және U ₂ бойынша V₁-ді анықтадық:

U₂ +V₁=C_21, 3+V₁=1, V₁=-2.

Потенциалдар анықталынып бітті. Енді бос торлардың сипаттамаларын (9) формула бойынша есептейік. 9-кестеден жоспардың оптималды емес екені белгілі болды, өйткені d₂₄ =-1<0.

Тұйық айналыс контурын (В₂А₄) торы үшін тұрғызайық:

Қайтадан жоғарыдағы келтірілген тәсілдерді пайдаланып, жаңа базистік шешім беретін кесте тұрғызамыз (10-кесте

Кесте 10

Минус таңбалы төбелердің бойында тұрған Х-тердің ең кішісі екі төбеде де бірдей 100-ге тең, яғни min{Х₂₂=100, Х₃₄=100}=100. Х₂₂-ның мәнін контур бойынша оң таңбалы төбелердегі шамаларға қосып, теріс таңбалы төбелердегі шамалардан алып тастағанда теріс таңбалы төбелерде нөлдер қалды. Сондықтан, осы торлардың бағалары С₂₂=4 және С₃₄=2 бойынша, мақсат функцияны жақсартатын кіші бағасы бар (В₃А₄)-ші торға нөл жазылады да, яғни тор толтырылған деп есептелінеді.

Сонымең мына төмендегі жаңа шешімді алдық:

Осы базиске сәйкес мақсат функцияның мәні:

Z = 1 *100 + 1 *300 + 2*100 + 3*500 + 1*100 = 2200.

Бұл табылған мән Z₂-нің мәнінен аз, яғни

d₂₄*Х₂₄=-1*100 = -100.

Сонымең мақсат функцияның мәні 100 теңгеге кемиді шешімді әлі жақсартуға бола ма, жоқ па? Оптималдық шартты тексерейік. Толтырылған торлар бойынша потенциалдардың U_i және V_j мәндерін тағайындайық:

Бос торлардың сипаттамаларын есептейік (11 –кесте

Соңғы оптималдық шартты тексергенде d_ij -лердің барлығы оң сандар, сондықтан есептің шешімі табылды.

У. Вогель (Фогель) әдісі

Транспорттық есептерді шешуге арналған бірнеше әдістер бар, бірақ олардың бір-бірінен айырмашылығы көп емес.

Қазіргі кезде тірек жоспарын құрғанда бірден немесе оптималдық шешімге өте жақын базистік шешімді құруға мүмкіндік беретін бірнеше әдістер белгілі. Солардың бірі аппроксимация әдісін қарастырайық. Ол осы әдістердің ішіндегі экономикалық тұрғыдан қарағанда ең ұтымдысы.

Ескерту: Аппроксимация ағылшынша түзету, жақындасу деген ұғымды білдіреді.

Аппроксимация әдісінің авторы американ математигі У. Фогель (кейбір ағылшын тілінен аударған оқу құралдарында У. Вогель деп аталынып жүр). Фогель әдісінің мазмұнын жай бір қарапайым есептің шығару тәсілі арқылы түсіндірейік.

Есеп. Есептің берілу шартын қарастырмай-ақ бірден оның матема-тикалық моделін жазайық:

Төмендегі шарттарды қанағаттандыратын:

мына мақсат функцияның минималды мәнін табу керек:

L = 8Х₁₁+ 6Х₂₁+ 10Х₃₁+ 9Х₁₂+ 5Х₂₂+ 7Х₃₂.

Шешуі: Берілген мәліметтер арқылы кесте құрамыз. Кестеге Фогель әдісінің талабы бойынша қосымша торлардың бағалар айырымдарының реттерін көрсететін бағана және жол тұрғызамыз.

Кестенің әр жолдарымен бағаналары үшін торлардың бағалар айырымдарының реттері есептелінеді. Ол үшін әр жолмен бағаналардың бағалары шамаларының өсу тәртібімен орналастырылады да, олардан өсу тәртібінің ретімен ең кіші бағаны алып тастап 1-реттегі айырымды, 2-реттегі айырымды тағы сол сияқты айырымдарды есептейді. Есептелген айырымдарды рет-ретімен кестеге (кесте жолдары бойынша айырымдарды қосымша бағанаға, ал

бағаналар бойынш; айырымдарды қосымша жолға) жазады.

Кесте 12

1-реттегі айырымдар бойынша матрица құрамыз да, олардың ішінен ең үлкенін таңдаймыз, яғни:

Табылған айырым 3-ке тең. Ол В₃ жолда. Егер оптималды тірек жоспарын құрғанда осы жолдағы ең кіші бағалы тор бірінші кезекте толтырылмаса, онда ең көп шығынға ұшыраймыз. Сондықтаң осы жолдағы ең кіші бағалы (В₃, А₂)- адресінде тұрған торды мүмкіндігінше максималды шамамен толтырамыз. Бұл жолда сұраныс b₃= 7000, ал қор а₂= 14000. Ең үлкен шама 7000 шектелгең оны (В₃, А₂)-торына жазамыз (кестені қараңыз).

Келесі қадамға көшу үшін В₃ - жолды кестеден сызып тастаймыз. 2-қадамда жаңа матрица құрамыз:

2-реттегі айырым бойынша екі максималды (4 және 4) айырым табылды, біреуі А₁ және екіншісі А₂ бағанасында жатыр. Мұндай жағдайда қай бағанада толтырылмаған кіші бағалы тор болса, сол торға максималды шама жазылады. Қарастырылып отырған есепте ол тор (В₂, А₂) бағасы 5-ке тең. А₂ пунктте қалған қордың шамасы: (14000-7000) =7000, осы мәнді (В₂, А₁) адрестегі торға жазамыз. Келесі максималды айырым (4) А₁ бағанада, онда (В₂, А₁) торы кіші бағалы (6) осы торға В₂ тұтынушының қалған сұранысын (8000-7000=1000) жазамыз (кестені қараңыз).

Әрі қарай жоғарыдағы баяндауға сәйкес соңғы (В₁, А₁) торына 10000 жазылады. Толтырылған торлардың саны-4, ал ол мына формула бойынша: K_m=m+n-1=2+3-1=4, яғни тірек жоспары дұрыс құрылды, базистік шешім алынды.

Есептің базистік шешімінің оптималдық жағдайын потенциалдар әдісімен тексерейік. Толтырылған торлар үшін мына формула бойынша потенциалдарды анықтайық:

(10)

Бірінші жолдың потенциалын α₁ = 0 деп қабылдап, кестенің қалған потенциалдарын алдыңғы тақырыптардағы келтірілген тәсілмен анықтадық (6.13-кесте қараңыз).

Базистік шешім оптималды делінеді, егер Z—>min (егер Z-> max ізделінсе, онда барлық тұжырым керісінше жүреді) болса және барлық толтырылмаған торлар үшін мына жағдай орындалса:

(11)

мұндағы c^б_ij -толтырылмаған торлардың бағалары.

Кестеде (В₁, А₂) және (В₃, А₁) торлары толтырылмаған бағалары: С₁₂= 9 және С₃₁= 10. Олай болса С₁₂  α₁ +β₂; 9>0+7және С₃₁  α₃ +β₁; 10 > 0 + 8. Сонымен базистік шешім оптималды.

Ашық транспорттық есеп

Біз алдыңғы тақырыпта жіберілетін жүктің қосымша қабылдау орын-дарына баратын жүктің қосындыларына тең болатын жағдайды қарастырған болатынбыз, яғни

мұндағы а_i(i=1,2,...,т) i-ші шаруашылықтан жіберілетін жүктің мөлшері, ал b_j(j=1.2,...,n) j-ші қабылдау орнына қажетті заттың (жүктің) мөлшері. Тәжірибелік есептерді шығарғанда көп жағдайларда а_i b_j болуы мүмкін. Транспорт есебіндегі мына жағдай:

орындалатын есептерді ашық транспорт есебі дейді. Кейде мұндаи транспорт есептерін баланс бермейтін есептер деп те атайды.

Транспорт есептерін шешуге арналған әдістердің барлығы (алгоритмдер) жабық транспорт есептері үшін жасалған. Сондықтан, ашық транспорт есептерін шешу үшін ресурсының мөлшері

болатын жасанды (жасалған) қабылдау пунктін немесе

көлемде қосымша өндіріс затын бере алатын жасанды (жасалған) өндіріс орындары қажет болады. Бірақ, бұл жағдайда жасанды қабылдау (өндіру) орындарына зат тасылмауы, ал жасанды өндіру орындарынан зат алынбауы керек. Бұл шартты орындау үшін жасанды бағана немесе жол бойынша орналасқан торлар бағасын (С_ij-ді) нөлге тең деп алу керек. Сонда ғана бұл жасанды торларға қанша сан жазылғанымен де, бұл торлар үшін С_ij, Х_ij= 0 болады, демек ол мақсат функцияға ешқандай өзгеріс енгізбейді. Басқаша айтқанда, жалған өндіріс орнынан зат алынбайды да жалған қабылдау орнына зат тасылмайды.

Сонымен біз ашық транспорт есебін жоғарыда көрсетілген жабық транспорт есебіне келтірдік, олай болса транспорт есептерін шешуге арналған әдістерді мұндай есептер үшін де пайдалануға болады. Ескерте кететін жағдай, ашық транспорт есебін жабық транспорт есебіне келтіргеннен кейін базистік шешуді тапсақ, онда базистік белгісіздердің саны m+n-1-ден кем болып қалуы мүмкін.

Егер базистік белгісіздердің саны m+n-1-ден кем болса, онда бұл шешудің оптималдығын тексеру және келесі базистік шешуге көшу мүмкін емес. Себебі, біріншіден, оптималдық тексеруге қажетті тік және жатық жолдардың коэффициенттері (U_i, V_j) толық табылмайды, демек бос торлар үшін d_ij-лерді тауып, таңбасын тексере алмаймыз. Екіншідең жаңа базиске көшуді ұйымдастыратын тұйық контур құрылмайды. Бұл жағдайда жазылған санның мөлшері нөлге тең болатын жалған (жасанды) торлар таңдап алынады. Жоғарыда айтылғандар түсінікті болу үшін төмендегі ашық транспорт есебін қарастыралық (есепте берілген сандық мәліметтер жуықтап алынған).

Мысал. Айталық төрт (А₁, А₂, А₃, А₄) жанармай қоймасынан үш (В₁ В₂, В₃) егістік орындарында жұмыс жасап жатқан техникаларға жанармай тасылмақшы. Әр қоймада жанармай мөлшері мынадай: а₁=500т, а₂=400т, а₃=500т, а₄=400 т, ал жанармай әр егістік орындарындағы техникаларға мынадай мөлшерде: b₁=400 т, b₂= 500 т, b₃= 300 т қажет. Жанармайды тасымалдау тарифы, яғни 1 тонна жанармайды әр қоймадан әр егістік орнына тасуға қажетті қаржы (С_ij) 13- кестеде келтірілген.

Кесте 13

Барлық техникаларды жанармаймен қамтамасыз етуге кететін транспорт шығыны ең аз (минималды) болу үшін қай қоймадан, қай егістік орындарындағы техникаларға, қанша мөлшерде жанармай тасу керек екендігін табу керек.

Берілген есептің математикалық моделін жазалық, ол үшін i-ші қоймадан j-ші егіс орталығына жеткізетін жанармай мөлшерін X_ij деп алайық. Құрылатын жоспар мына шарттарды қанағаттандырсын:

- барлық қоймалардан жанармайды тасымалдауды:

- әр егістікте жұмыс жасап жатқан техникаларды тиісті көлемде жанармаймен қамтамасыз етуді:

- белпсіздердің теріс шама болмау шартын: х₁₁о,х₁₂о,х₁₃о...х₄₃о. Осы жағдайларда мына мақсат функцияның

минималды мәнін табу керек.

Бұл есеп ашық транспорт есебіне жатады, себебі а_ib_j , яғни

Есепті шешу үшін кесте құрып, жоғарыда айтылған алгоритмді пайдаланып және а_i >b_j болғандықтан қажетті жанармай мөлшері 600 тоннаға тең жалған қабылдау пунктін енгіземіз де, бұл пунктте қатынас қаражаттарын нөлге тең етіп аламыз (С₁₄=С₂₄=С₃₄=С₄₄=0). Сонымен, құрылған кесте бойынша ашық транспорт есебі жабық транспорт есебіне айналды. Олай болса, жоғарыда келтірілген жабық транспорттық есептерді шешуге қолданылатын алгоритмдерді пайдаланайық.

Алғашқы базистік шешуді табу үшін min(С_ij)-лерді пайдалансақ, min(С_ij)= С₂₃= С₄₂= С₄₃= 2, олай болса Х₂₃= тіп (а₂b₃) = 300.

Сонымен, үшінші егістіктегі техникалар жанармаймен толық қамтамасыздандырылады. Келесі минималды бағалы тор: Х₄₂= тіп (а₄, b₂) =min (400,500)=400, яғни екінші егістіктегІ техникаларды толық қамтамасыз ету үшін әлі 100 т жанармай жетпейді, ол майды қай қоймадан алу керек екендігін білу үшін сол тік жолда жатқан С_ij-лердің ішіндегі минимумын табамыз. Ол С₂₂= 3, ендеше: Х₂₂= тіп (а₂ - Х₂₃, b₂-Х₄₂) = тіп (400-300, 500-400)=100. Сонымең екінші егістіктегі техникалар жанармаймен толық қамтамасыз етіледі. Енді бірінші егістіктегі техникаларға жанар-майды тек 1-ші және 3-ші қоймалардан ғана алады. Өйткені, қалған қоймадағы жанармайлар толығымен тасылып әкетілді. Бұл екі қойманың қайсысынан алу керек екендігін білу үшін қатынас қаражаттарын салыстырып, кішісін аламыз.

Кесте 14

Яғни С₁₁= 5, С₃₁=4, демек Х₃₁=min(а₃,b₁,)=min(500,400)=400. Сөйтіп барлық техникалар жанармаймен қамтамасыз етілді: Х₂₂= 100, Х₂₃=300, Х₃₁=400, Х₄₂=400. Былайша айтқанда, 1-егістіктегі техникаларға (Х₃₁) 3-қоймадан -400 т, 2-егістіктегі техникаларға (Х₂₂, Х₄₂) - 2-қоймадан -100 т, 4-қоймадан - 400 т, ал 3-егістіктегі техникаларға (Х₂₃) 2-қоймадан 300 т тасылды. Бұл шешуде кететін шығын:

Z=4*400+3*100+2*300+2*400=3300

Табылған шешім базистік шешімді бере ме? Жоқ па? Ол үшін базистік торлар санын есептейміз. Табылған шешім базистік шешім болуы үшін толтырылған торлардың саны m+n-1 болу керек, яғни 4 + 4-1=7.

Біздің жағдайымызда 4 < 7. Демек табылған шешім базис бола алмайды, олай болса U₁ және V_j -лер толық табылмайды. Шешу базистік болу үшін жалған торларды толтыру керек. Қарастырылып отырған есеп бойынша ол торлар: (А₁, В₄) - Х₁₄ = 500; (А₃, В₄) - Х₃₄ = 100 және (А₃,В₂)-Х₃₂=0.

Себебі 1- қоймадан әлі жанармай алмадық, ал 3-қоймада әлі 500 т май бар. Оның 400 т алып кеттік те, 100 т қалып қойды. Бұл екі торды базиске енгізгеннің өзінде де транспорттық есептің бірінші шарты орындалмай қалады, яғни 6<7, сондықтан нөлмен толтырылатын және бағасы ең үлкен (А₃, В₂) тор толтырылған деп есептейміз. Енді 7=7 болды, табылған шешу базистік бола алады, демек U₁ менV_j -лерді таба аламыз, яғни

U₁ +V_j =C_ij

(A₁,B₄) торы үшін U₁+V₄=C₁₄; U₁=0 десек бұдан V₄=0

Сонымен, толтырылған торлар үшін жолдардың және бағаналардың коэффициенттерін таптық. Енді бос торлар үшін мына жағдайды тексерейік:

Барлық бос торлар үшін қойылған шарт орындалды, яғни d_ij=С_ij-U_i-V_j барлығы оң таңбалы (d_ij>0), демек жоғарыда табылған базистік шешім оптималды шешім.

Дәріс 7. Тақырып: Гомори тіліктердің әдісі.

Гомори тіліктердің әдісі. Квадратты мақсаттық функциялар.

«Кесiп тастау» әдiсiнiң мәнiсi сызықтық бағдарламалау есебiнiң шешiмi бола алатын аймақ (ШБА) құрайтын көпбұрыштың, координаты бүтiн сандар болмайтын төбесiн кесiп тастауында. Бұл кезде координаттары бүтiн сандар болатын барлық нүктелер (ШБА)-да жаңа көпбұрышта қалады. Бiрнеше әрекеттен кейiн мұндай нүктелер шеткi төбелерге жетедi де, координаттары бүтiн санды төбелердiң бiреуiнде бүтiн санды оптималды жоспар алынады.

Кесiп тастау әдiсiнiң идеясы бойынша: (7.1)-(7.4) есептiң (7.4) шарты алынып тасталады да, (7.1)-(7.3) есебi шығарылады.

Егер (7.1)-(7.3) есебiнiң оптималды шешiмiнде X* белгiсiздерге қойылған олардың бүтiн сан болу талабы орындалса, онда бұл шешiм бастапқы (7.1)-(7.4) есебiнiң де шешiмi бола алады.

Егер оптималды X* шешiмде бүтiн сан болу талабы орындалмаса, онда шектеулер жүйесiне қосымша сызықты шектеу енгiзiледi. Бұл шектеу (7.1)-(7.4) есебiнiң барлық талабын қанағаттандырады, ал оптималды X* шешiмдi қанағаттандырмайды деп есептелiнедi. Сөйтiп, қосымша сызықты шектеудiң гипержазықтығы, оптималды шешiмдi (X*) есептiң (7.1)-(7.4) бүтiн санды жоспарынан «кесiп тастайды» делiнедi.

Гипержазықтық (7.1)-(7.4) есептiң шартына қосылады да, бүтiн санды - сызықтық бағдарламалау есебi алынады. Есеп жоғарыдағы келтiрiлген амалдармен қайтадан шығарылады.

Осы есептi шығаруға сызықтық бағдарламалау аппаратын қолданатын басқа да жолдар бар. Бiрақ барлық жағдайларда қосымша сызықтық шектеулер тұрғызылады. Есептеу жұмысының аяқталуы қамтамасыз етiледi, қосымша сызықты шектеулер көбейiп кетпеуi үшiн, әртүрлi амалдар жасалынады. Сөйтiп, осы мәселелер әр алгоритмде әртүрлi шешiледi. Айталық, алынған бүтiн санды оптималдық шешiмде: Х_опт =(b₁,b₂,...,b_r, 0,...,0) симплекс кесте мына түрде болсын:

мұндағы r - шектеулер жүйесiнiң рангi;

а_i,r+1 – і-жолымен (r+1) - бағанасының қиылысатын жерiндегi симплекс кестенiң коэффициентi;

b_i - i-жолының бос мүшесi.

Айталық, b_і және a_ij (і=1,...,r; j= r+1,...,n) кем дегенде бiреуi - бөлшек сан.

Осы b_i және а_ij сандарының бүтiн бөлiктерiн былай [b_i] және [a_ij] белгiлейiк.

Анықтама. b_і - санның бүтiн бөлiгi деп, өзiнен аспайтын ең үлкен бүтiн санды [b_i] айтады.

Егер b_і және а_ij сандарының бөлшек бөлiмiн {b_і} және {а_ij} арқылы белгiлесек, онда оларды былай анықтауға болады:

{b_і} = b_і - [b_i] және {а_ij} = а_ij- [а_ij]

Мысал. Мына сандардың бүтiн және бөлшек бөлiмдерiн жазайық: 4/5; 8/3; -4/5 және -8/3.

Егер b_і және а_ij сандарының кем дегенде бiреуi бөлшек сан болса, онда санның бүтiн және бөлшек бөлiгiнiң жоғарыдағы қабылданған белгiлерiн ескере отырып, бүтiн сандық қосымша шектеудi былай көрсетуге болады:

{а_i,r+1}Х_r+1+ {а_i,r+2}Х_r+2+ ... + {а_in}Х_n ≥ {b_i}.

Ескерту: 1) Егер b_i - бөлшек сан, ал барлық а_ij - бүтiн сандар болса, онда есептiң бүтiн сандык шешiмi болмайды.

2) Бүтiнсандық шектеулер барлық айнымалыларға койылмай, тек бiр бөлiктерiне қойылуы мүмкiн. Мұндай кезде есеп толық емес бүтiнсанды деп аталады.

Есептi графиктiк әдiспен шешу

Бүтiнсанды бағдарламалау есебiн графиктiк әдiспен шешу алгоритмi сызықтық бағдарламалау есебiн шешу алгоритмiне ұқсас.

Х₁ОХ₂ координаттар жүйесiнен шешiмi бола алатын аймақты тапқаннан кейiн, деңгей сызығын және С векторын тұрғызады. Максимумға iзделiнетiн есеп үшiн деңгей сызығын С векторының бағытымен жылжыта отырып, координат жүйесiнiң бас өсiнен ең қашықта орналасқан нүктенi тауып, оның координаттарын анықтайды.

Осы нүктенiң координаттары бүтiн сандар болмаған жағдайда, шешiмi бола алатын аймақта бүтiнсанды тор құрылады және одан, мақсат функциясының мәнi бүтiнсандық емес шешiмдегi экстремалдық мәнiне ең жақын және шектеулер жүйесiн қанағаттандыратын бүтiнсанды төбелердi, яғни тордың бұрыштарының координаттарын анықтайды. Осы бұрыштардың координаттары бүтiн санды шешiмдердi бередi.

Минимумге iзделiнетiн есептiң де геометриялық тәсiлмен шығарылу жолы осылай жүргiзiледi. Бiр есеп карастырайық.

Есеп. Өзiнiң финанстiк жағдайын жақсарту үшiн, фирма бәсекелесуге қабiлеттi өнiмдi өндiрудi көбейтуге шешiм қабылдады.

Ол үшiн цехтардың бiреуiнен қосымша жабдықтар орнатуға ауданы 19/3 м² орын бөлiндi және қосымша жабдықтарды сатып алуға фирма 10 мың доллар қаражат жұмсамақшы.

Фирманың екi түрлi жабдық сатып алуға мүмкiншiлiгi бар. 1-шi түрлi жабдықтың 1 комплектiсi 1.0 мың доллар, ал 2-шi түрi - 3 мың доллар. 1-шi түрлi жабдықтың 1 комплектiсi сатып алынса, бiр тәулiкте өнiмдi 2 дана өсiруi мүмкiн, ал 2-шi түрiнiң 1 комплектiсi -4 данаға өсiредi. 1-шi жабдықтың 1 комплектiсiне 2 м² орын, ал 2-шi жабдықтың 1 комплектiсiне 1 м² орын керек.

Фирма өнiмдi максималды өндiруге мүмкiншiлiк жасау үшiн қандай құрамда және қанша комплект жабдықтардың түрлерiн сатып алуы қажет?

Шешiмi. Есептiң математикалық моделiн құрайық. Айталық, фирма 1-шi түрлi жабдықтың Х₁ комплектiсiн, ал 2-шi түрлi жабдықтың Х₁ комплектiсiн сатып алмақшы. Олай болса, есептiң математикалық моделi:

Z(х) = 2х₁ + 4х₂ → mах

мына шектеулерде:

Екi белгiсiзi бар бүтiнсанды бағдарламалау есебiн алдық. Есептiң шешiмiн графиктiк тәсiлмен табайық (7.1-сурет).

ОАВС - шешiм бола алмайтын аймақ (ШБА). Есеп В(27/15; 41/15) нүктесiнде оптималды шешiмге жетедi. Бұл нүктеде мақсат функциясының мәнi Z=218/15 бiрлiк. Алынған оптималдық шешiм бүтiн санды емес. Берiлген есептiң шешiмiн анықтау үшiн, ОАВС көпбұрышты ОКЕМNF көпбұрышымен ауыстырамыз. Бұл көпбұрыш берiлген есептiң шешiмi бола алатындай барлық нүктелердi қамтыған.

С(2;4) векторын құрайық. Деңгей сызығын осы вектордың бағытымен жылжытып отырып, Е (1; 3) нүктесiн алдық. Бұл нүктеде мақсат функциясының оптималды мәнi:

Z (Х_6үm)_mах=2.1 +4.3 = 14 бiрлiгi

Сонымен фирма 1-шi түрлi жабдықтың бiр комплектiсiн, 2-шi түрлi жабдықтың үш комплектiсiн сатып алғанда, бiр тәулiкте өндiретiн өнiмiнiң ең максималды мәнi 14 бiрлiгiне жетедi.

Гомори әдiсiнiң алгоритмi

1. Белгiсiздердiң бүтiнсандық болу талабы қарастырылмай, симплекс әдiсiмен оптималды жоспар табылады.

2. Егер табылған оптималды жоспар бүтiнсанды болса, онда есептеу тоқтатылады.

Егер симплекс кестеде кем дегенде бiр бөлшек сан болса (яғни кем дегенде бiр айнымалының мәнi бөлшек сан болса), онда бүтiнсандық талапқа қосымша шектеу енгiзiледi.

Қосымша шектеу (теңсiздiк) кiргiзу ережесi

а) бөлiм бөлiгi ең үлкен айнымалы таңдап алынады (яғни бөлшек санның бөлiмi ең үлкен бос мүше орналасқан симплекс кестедегi жол анықталынады);

б) осы жолдың әр коэффициентiнен өзiнен аспайтын ең үлкен бүтiн сан алынып тасталады (осы алынған санды d_ij деп белгiлейдi);

в) табылған сандар d_ij жаңа қосымша шектеудiң өздерiне сэйкес айнымалылардың коэффициенттерi болып есептелiнедi, ал d_i0 саны - осы шектеудiң бос мүшесi, ягни теңсiздiктiң оң жағындағы сан;

г) жаңа шектеудiң түрi « ≥» (кем емес);

д) қосымша (теңсiздiк) шектеу теңдiкке айналдырылады және теңдiктiң екi жағы да (-1)-ге көбейтiледi, осы шектеуге енгiзiлген айнымалы симплекс кестенiң базистiк баганасына және түрлендiрiлген шектеудiң барлық коэффициенттерi кестеге жазылады.

3. Кестедегi жаңа жол бағыттаушы жол ретiнде қабылданады да, осы жол үшiн қосалқы симплекстiк қатынас есептелiнедi, яғни терiс емес бағалардың (∆_j) мiндеттi түрде терiс коэффициенттерге қатынасы есептелiнедi. Оның абсолюттiк шамасы, яғни ең кiшi қатынас бойынша бағыттаушы бағана таңдап алынады.

4. Таңдап алынған бас элемент бойынша (симплекс әдiсi сияқты) түрлендiру бiр ретте орындарын ауыстыру жүргiзiледi.

Әрi карай алгоритм 2-пункттен бүтiнсанды оптималды жоспар алынғанша қайталана бередi. Сонымен Гомори алгоритмi аяқталды.

Дәріс 8. Тақырып: Графтар теориясының әдістері және модельдері.

Графтар теориясының әдістері және модельдері. Графтар және графтарда типтік есептер.

Назарыңызға. Егер бағыттаушы жолда айнымалылардың бiрде-бiр терiс таңбалы коэффициентi болмаса, онда есептiң шектеулер жүйесi бүтiнсанды шешiм аймағында бiрiкпеген, есептiң шешiмi жоқ.

Мысал.Z = х₁ + 3х₂ → mах мына шектеулерде

Шешiмi. Бүтiнсандық шартты ескермей, есептi симплекс әдiсiмен шығарамыз. Ол үшiн есептiң моделiн канондық түрге және М-есебiне ауыстырайық:

Есептi симплекс кестесiне жазамыз (7.1-кесте). Кестенiң ∆_j жолындағы элементтер мына формула бойынша анықталды:

∆_j = ∑а_ijс_i - с_j

∆₁= 1∙(-М)+4∙0 + 2∙0-0 = -М-0 және т.б. с.с.

7.1-кесте

№1	Сi	0	1	3	0
Сi	Ба	bi	X1	Х2	Хз
-М	У1	1	1	1	-1	1:1 = 1 
0	Х4	4	1	2	0	4:2 = 2
0	Х5	2	-1	2	0	2:2=1
z	∆j	0 -М	-1 -M	-3 -M	0 M

№4-шi симплекс кестеде есептiң оптималды шешiмi алынды (7.2-кесте).

№4	Сi	0	0	-М	0
Сi	Ба	bi	Х4	У1	X5
3	Х2	3/2	1/4	0	1/4
1	X1	1	1/2	0	-1/2
0	Хз	3/2	3/4	-1	-1/4
Z	∆j	11/2	5/4	M	1/4

Жалған айнымалы У₁=0 болуына байланысты оны кестеден алып тастап, келесi есептеулерде ескермеймiз.

Х₂ және Хз айнымалылар бөлшек сандар, яғни бүтінсанды шарт орындалмаған. Ендi осы екi айнымалының бiреуiнiң жолына бүтiнсандық шектеу енгiземiз (себебi екеуiнiң де бөлшек сандары бiрдей, кез келгенiн алуға болады).

Х₂ айнымалының жолына қосымша шектеу енгiзейiк, онда мынадай коэффициенттер болуы керек: d₁₀=b₁=3/2-1=1/2, мұндағы 1-осы санның b_i=3/2-ден асып кетпейтiн ең максималды бүтiн бөлiгi.

Олай болса, қосымша шектеу: 1/4Х₄ + 1/4 Х₅≥ ½

Канондық түрге келтiрейiк: 1\4Х₄+1/4Х₅-Х₆=1/2 (-1)-ге көбейткеннен кейiн: -1/4Х₄-1/4Х₅+Х₆=-1/2, кестеге жазамыз (7.3-кесте). 7.3-кесте

№5	Сi	0	0	0
Сi	Ба	bi	Х4	Х5
3	Х2	3/2	1/4	1/4
1	Х1	1	1/2	-1/2
0	Хз	3/2	3/4	-1/4
0	Х6	-1/2	-1/4	-1/4	r 
Z	∆j	11/2	5/4	1/4
қск			-5	-1
↑ k

№5 симплекс кесте өзiнiң оптималды жағдайын жоғалтты, себебi терiс таңбалы бос мүше пайда болды.

Жаңа жолды бағыттаушы жол ретiнде кабылдап, ∆j жолындағы терiс емес элементтердiң бағыттаушы жолындағы мiндеттi түрде терiс элементтерге қатынасын есептеймiз де, қосалқы симплекс қатынасын анықтаймыз, яғни:

Абсолюттiк шамасы ең кiшi ҚСҚ х_і бойынша бағыттаушы бағананы таңдаймыз. Есепте ол Х₅ - бағанасы. Кестенi бiр рет орнын ауыстырып түрлендiрудiң нәтижесiнде мынадай 7.4-кесте алынды: 7.4-кесте

№6	Сj	0	0	0
Сi	Ба	bi	Х1	Х6
3	Х2	1	0	1
1	Х1	2	1	-2
0	Х3	1	1/2	-1
0	Х5	2	1	-4
z	∆j	5	3/2	1

Кестеде барлық ∆j>0 және айнымалылардың коэффициенттерi бүтiн сандар, демек жаңа оптималды шешiм табылды.

Оптималды жоспар: Х(2; 1; 1; 0; 2; 0) және Z=5 (немесе х₁₌2; х₂=1 ; х₃=1; x₄=0; х₅=2 және х₆=0).

Есептiң графиктiк шешiмi де симплекс әдiсіпен алынған шешiмнiң дұрыстығын дәлелдейдi (7.2-сурет).

Шешiмi бола алатын аймақ құрайтын көпбұрыштың төбелерiнiң координаттары: А(0; 1), В(3/2; 1), С(4; 0) және Д(l; 0). Оптималдық шешiмдi В'(2, 1) төбесiнiң координаттары бередi.

Дәріс 9. Тақырып: Қысқа жолы мен Дейкстра әдісі.

Қысқа жолы мен Дейкстра әдісін құрылыс міндеті. Желілер мен сақтау принциптері қозғалысы.

Желілік модель желінің өзгеше түрінде берілген кейбір өзара байланысқан жұмыстар кешенің орындалу жоспарын ұсынады. Графикалық түрде бейнеленуін желілік графигі деп атаймыз. Желілік моделдің өзгешелігі алда болатын жұмыстардың барлық уақытша өзарабайланысын айқын аңықтау болып табылады.

Желілік моделдің негізгі элементтері ол жағдай және жұмыс.

ЖЖБ-да жұмыс термині кең мағынада қолданылады. Біріншіден, бұл нағыз жұмыс — қордың шығының талап ететін ұзына бойы уақыт бойынша процесс (мысалы, бұйымды жинау, және т.с.с.). Әрбір нағыз жұмыс нақты, дәл сипатталған және жауапты орындаушы болу керек.

Екіншіден, бұл тосу — еңбек шығының талап етпейтін ұзына бойы уақыт бойынша процесс (мысалы, сырлағаннан кейінгі кептіру процессі, металлдың ескіруі және т.с.с).

Үшіншіден, бұл тәуелділік немесе жалған жұмыс — еңбек шығының, материалдық қорды немесе уақытты талап етпейтін екі немесе бірнеше жұмыстар арасындағы логикалық байланыс. Ол бір жұмыстың мүмкіншілігі екінші жұмыстың нәтижесіне байланысты екенін көрсетеді. Әрине, жалған жұмыстың ұзақтылығы тең нөлге деп қабылданады.

Жағдай — жоба орындалуының жеке кезеңін көрсететін қандай да бір процестің аяқталу сәті. Жағдай жеке жұмыстың жеке нәтижесі немесе бірнеше жұмыстың қосындылар нәтижесі болуы мүмкін. Жағдай оның алдындағы барлық жұмыстар біткенен кейін аяқталуы мүмкін. Келесі жұмыстар тек жағдай аяқталғаннан кейін басталуы мүмкін. Осыдан жағдайдың қосалқы сипаты: барлық тура бұрынғы жұмыстар үшін – соңғы, ал барлық келесілерө бастапқы. Жағдайда жалғасы жоқ деп жорамалданады және тез арада аяқталады. Сондықтан желілік моделге кіретін әрбір жағдай толық, дәл және жан-жақты аңықталған, оның тұжырымдамасы өзіне барлық тікелей оған бұрынғы жұмыстардың нәтижесін енгізу керек.

Желілік моделдің жағдайлар арасында алғашқы және аяқтайтын жағдайларды бөледі. Алғашқы жағдайда ұсынылған жұмыс кешенінің моделіне жататын бұрынғы жұмыстар мен жағдайлар жоқ. Аяқтайтын жағдайда келесі жұмыстар мен жағдайлар жоқ.

Желілік графикте жағдайлар –дөңгелек (графтың төбелері) түрінде, ал жұмыстар — жұмыстар арасындағы байланыстарды көрсететін стрел­камен (бағытталған доға). Желілік графиктін фрагменттері 1. суретте көрсетілген.

Сурет1

Сурет 2

Сурет 2, а суретте кейбір экономикалық объектінің тиімді жоспарын құру және үлгілеу есебінің желілік графигі көрсетілген. Бұл есепті шешу үшін келесі жұмыстарды орындау керек: А — зерттеу проблемасын тұжырымдау; Б — зерттелетін объектінің математикалық моделін құру; В — ақпарат жинау; Г — есепті шешу әдісін таңдау; Д — ЭЕМ үшін программаны құру және түзету; Е — тиімді жоспарын есептеу; Ж — тапсырыс берушіге есептің нәтижесін беру. Графикте циф­рлармен осы сәйкес жұмыстардыңорындалуына әкеп соқтыратын жағдай нөмірлері белгіленген.

Желілік моделде сандық бағалар жоқ. Мұндай желіні құрылымдық деп атайды. Бірақта тәжірибеде жұмыстың ұзақтылығының бағасы берілген желілер қолданылады (сәйкес стрелкалардың қасында сағат, апта ай т.б. түрінде), сонымен бірге басқа параметрлердің бағасы, мысалыкөп еңбекті, бағасын және т.с.с. Осындай түрдегі желілерді біз болашақта қарастырамыз.

Желілерді құрудың басқа принципі болу мүмкін- ол жағдайсыз. Мұндай желіде граф төбелері (мысалы, тіктөртбұрыш түрінде бейнеленген) нақты жұмыстарды білдіреді, ал стрелкалар — орындалу ретін анықтайтын осы жұмыстар арасындағы тәуелділік. Мысал ретінде кейбір экономикалық объектінің тиімді жоспарын үлгілеу және құру есебінің "жағдай — жұмыс" желілік графигі, 14.2 а, суретінде келтірілген "жұмыс — байланыс" желі түрінде көрсетілген сурет 14.2 б.

Дәріс 10. Тақырып: Желілік модельдеу есебі.

Ең үлкен ағымдар және ең кішкентай кесіктер. Желілік модельдеу есебі. Тармақтар және шекаралар есебі.

ЖЖБның қолдану саласы мен міндеті

Күрделі процестерді жоспарлаудың ең тиімді тәсілдерін іздеу желілік жоспарлау мен басқарудың жаңа әдістеріне әкелді (ЖЖБ).

ЖЖБ әдістердің жүйесі — ірі халықшаруашылық кешеннің, ғылыми зерттеудің, конструкторлық және технологиялық өндірісті дайындығын, жаңа бұйымның түрлерін, құрылыс пен қайта құру, желілік графиктерді қолданып негізгі қорларда ремонт жасаудың өндеуін басқару және жоспарлау әдістер жүйесі.

Желілік графиктерді қолданатын алғашқы жүйелер, 50-ші жылдың соңында АҚШ-та қолданды және CPМ (ағылшыннан, қиын-қыстау жолының әдісі білдіреді) және PERT {программаны бағалау және шолу әдісі) деп аталды. СРМ жүйесі алғашқы рет құрылыс жұмыстарын басқару кезінде, ал PERT жүйесі— "Поларис" жүйесін өндеу қолданды.

Желілік жоспарлау бойынша жұмыстар Ресейде 60-шы жылдарда басталды. Онда ЖЖБ әдістері құрылыс пен ғылыми өндеулерді қолданыс тапты. Келешекте желілік әдістер халық шаруашылығының басқа салаларында да кең қолдана бастады.

ЖЖБ желілік график арқылы процесті үлгілеуге негізделген және жұмыс кешенін басқару және жоспарлау бойынша ұйымдастырушылық және бақылау шаралар, есептеу әдістерінің жиынтығы болып саналады.

ЖЖБ жүйесі мынаған мүмкіндік береді

• Кейбір жұмыс кешеннің іске асыру календарлық жоспарын қалыптастыру;

• Уақыт резервін, еңбек, материалдық және ақшалық қорларды айқындау және жасақ жию;

• Жұмыс жүрісі кезінде мүмкіншілік кедергілерді ескерту және болжауымен "жетекші түйін" принципі бойынша кешендермен басқаруды жүзеге асыру;

• әртүрлі деңгейдегі және жетекшілер және жұмысты орындаушылар арасында жауапкершілікті дәл бөлу кезінд басқару тиімділігін көтеру.

ЖЖБ қолдану аралығы кеңірек: жүздеген ұйымдар мен мындаған адамдар қатысатын жеке тұлғалардың қызметіне қатысты есептерден бастап жобаларға дейін .

Жұмыс кешені деп оны орындау үшін үлкенсанды әртүрлі жұмыстарды жүзеге асыру керек әртүрлі есептерді түсінеміз. Ол бір ғимараттың, ұшақтын немесе басқа күрделі объектінің құрлысы болуы мүмкін.

Мындаған жеке зерттеулер мен операциялардан тұратын үлкен және күрделі жобалардың жүзеге асыруының жұмыс жоспарын құру үшін оны кейбір математикалық модель арқылы суреттеу керек.Жобаны суреттеудің мұндай тәсілі желілік модель деп аталады.

Желілік графиктерді құру ережесі мен реті

Желілік график жоспарлаудың бастапқы кезеңінде құрылады. Ең алдымен жоспарланған процесс жеке жұмыстарға бөлінеді, жұмыс пен жағдайдың тізімі құрылады, олардың логикалық байланысы мен орындалу тізбегі ойластырылады, жұмыстар жауапты орындаушыларға бекітіледі. Олардың көмегімен әрбір жұмыстың ұзақтылығы бағаланады. Содан кейін желілік график құрылады. Желілік графикті реттегеннен кейін жағдай мен жұмыстың параметрлері есептелінеді, уақыт резерві және қиын-қыстау жолы анықталады. Және ең соңғысы желілік графиктің талдауы мен оптимизациясы жүргізіледі, қажет жағдай кезінде жағдай мен жұмыстың параметрлерін қайта есептей отыра басынан бастап сызады.

Желілік графикті құру кезінде келесі ережелерді сақтау керек.

1. Желілік моделде "тұйықталған" жағдайлар болмау керек, яғни аяқталатын жағдайдан басқа бір де бір жұмыс шықпайтын жағдайлар (сур. 14.3 а)

2. Желілік графикте бір жұмыс алдыңда болмайтын "құйрықты" жағдайлар болмау керек {алғашқыдан басқа) (жағдай 3 — сурет 14.3 б).

3. Желіде тұйық контурлар мен жіптер болмау керек, яғни кейбр жағдайларды өздерімен біріктіретін жолдар (сур. 14.3 в, г)

4. Кез келген екі жағдай бірден кем емес жұмыс- стрелкамен байланысу керек (сур. 14.3 д, е)

5. Желіде бір алғашқы және бір аяқтайтын жағдай болу керек (сур 14.3 з)

Желілік графикті реттеу. Жолдар туралы түсінік

Бір жобаны құру үшін 12 жағдай бөлінді: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 және 24 олардың жұмысын байланыстыратын: (О, I), (0, 2), (О, 3), (1, 2), (1, 4), (1, 5), (2, 3), (2, 5), (2, 7), (3, б), (3, 7), (3, 10), (4, 8), (5, 8), (5, 7), (б, 10), (7, б), (7, 8), (7, 9), (7, 10), (8, 9), {9, 11), (Ю, 9), {10, 11). Желілік графикті құрып және реттеу керек. Желілік графиктін алғашқы жағдайы 0 (ему не предшествуют никакие рабо­ты), ал аяқтайтын жағдай 11 (за ним не следует ни однаработа). Желілік графиктерде сол жақтан он жаққа қарай уақыт өзгеруін ескере отырып, 0 жағдайын графиктін сол жағына орналастырамыз, ал 11 жағдайын — оң жаққа , олардың араларында ағымдағы жағдайларды олардың нөмірлеріне сәйкес бір реттпен орналастырамыз (рис. 14.4). Жағдайларды жұмыс тізімімен сәйкес жұмыс-стрелкалармен байланыстырамыз

Құрылған желілік график оның құрылуына қойылған тұжырымдалған ережелерге сәйкес келеді . Бірақ график реттелмеген.

Желілік графиктін реттелуі жағдай мен жұмыстарды мына түрде орналастыратын кез келген жұмыс үшін алдындағы жағдай сол жаққа қарай орналастырылған және осы жұмысты аяқтайтын жағдаймен салыстырғанда ең кіші нөмірі бар. Басқа сөзбен айтқанда, реттелген желілік графикте барлық жұмыс –стрелкалар сол жақтан оң жаққа қарай бағытталады: кіші нөмірі бар жағдайдан бастап үлкен нөмірлі жағдайға дейін.

Графикте орналастырумен сәйкес жағдай нөмірлерін өзгертеміз және реттелген желілік графикті аламыз (сур. 14.6), онда стрелкалар астында сәйкес жұмыстың ұзақтылығы көрсетілген (тәулікте).

Желілік графиктін ең негізгі түсінігі — ол жол. Жол — әрбір жұмыстың соңғы жағдайы одан кейінгі келесі жұмыстың бастапқы жағдайымен сәйкес келетін кез келген жұмыстар тізбегі. Желілік графиктін әртүрлі жолдар арасында толық жол L бар — басы желінің алғашқы жағдайымен, соңы- соңғысымен сәйкес келетін кез келген жол.

Желілік графиктегі ең ұзына бойы толық жолды қиын-қыстау деп атаймыз. Осы жолда орналасқан жағдай мен жұмыстарды да қиын -қыстау деп аталады.

Мысалы , қарастырылып отырған желілік графиктін толық жолдары мыналар болады 0→1→2→7→10→11 ұзына бойы 8+9+3+5+13=38 тәулік, жол 0→1→3→4→6→10→11 ұзына бойы 8+4+10+3+5+13=43 тәулікпен, жол 0→5→8→9→11 ұзына бойы 9+10+4+17=40 тәулікпен, жол 0→3→5→6→9→10→11 ұзына бойы 13+7+9+13+6+13=61 тәулікпен және т.с.с.

Қиын-қыстау жолдың ұзына бойы 61 тәулікті құрайды, яғни жұмыс кешенің өткізу үшін 61 тәулік қажет. Кешенді тез орындауға болмайды, өйткені жағдайды аяқтайтын жетістігіне жеті үшін міндетті түрде қиын- қыстау жолды өту керек.

Қиын- қыстау аңықтап, біз желінің қиын- қыстау жағдайлары 0, 3, 5, 6, 9, 10 және 11 мене қиын- қыстау жұмысын (0_>3)_>(3,5),(5,6),(6,9),(9,10)ЛЮ,11) орнаттық

Дәріс 11. Тақырып: Ойындар теориясы.

Ойындар теориясы. Ойында стратегиялар. Шығындар функциясы. Ойының бағасы. S-ойыны. Минимакс туралы теорема. 2х2 ойындар. 2хN ойындар. Графикалық түрде шешу.

Негізгі түсініктер.

Ойын теориясы, зерттеу пәні дау жағдайда шешімдерді қабылдау әдістері болып табылатын математикалық пәнді ұсынады

Практикада көптеген тапсырмалар кездеседі, оларға анықталмаған шарттарда шешім қабылдау қажет, яғни, екі жақ әртүрлі мақсаттарды көздейтін, ал нәтижелері әрбір серіктесінің әрекетіне байланысты болатын жағдайлар кездеседі. Шахмат, шашки, домино және т.б. ойын кезінде пайда болатын жағдайлар дау жағдайлар деп аталады: ойыншының жүрісі серіктесінің қадамына байланысты, ойын мақсаты- серіктестерінің біреуінің жеңісі. Экономикада дау жағдайлар жие кездеседі және оның әртүрлі сипатталуы бар. Оларға мысалы, жабдықтаушы мен тұтынушының арасындағы, сатушы мен сатып алушы арасындағы, банк пен клиенттің арасындағы қатынастар кіреді. Барлық осы жағдайларда дау серіктестерінің өз талаптарын орындауға, әрбіреуінің өзіне тиімді мақсатқа жеткізетін шешім қабылдаудан пайда болады. Және де әрбіреуіне тек өзінің мақсатымен ғана емес, сондай-ақ, серіктесінің мақсатымен есептесу, серіктестерінің шешімдерін алдын ала еске алу қажет.

Дау жағдайларда шешімді сауатты шешу үшін ғылыми негізделген әдістер қажет. Мұндай әдістер дау жағдайлардың математикалық теориясымен өңделген және ойындар теориясы деп аталады.

Ойындар теориясының негізгі түсініктерімен танысайық. Дау жағдайының математикалық моделі ойын деп аталады, дауда қатысатын жақтар –ойыншылар деп аталады, ал ойынның негізі-ұтыс болып келеді. Әрбір ойын үшін ережелер қалыптасады, яғни, шарттар жүйесі, олар мынаны анықтайды: 1) ойыншылар әрекеттерінің нұсқаларын; 2) әрбір ойыншының серіктесі туралы көлемді ақпараттың болуы; 3) әрбір әрекеттер жиыны әкелетін ұтыстары. Ереже бойынша, ұтыс (немесе ұтылыс) санаулы тәсілмен беруге болады; мысалы, ұтылысты-нөлмен, ұтысты-бірмен, ал тепе-теңдікті-1/2.

Ойын ойыншылар тәртібін сипаттайтын ережелер жиынтығын құрайды. Басынан бастап соңына дейін кейбір нақты түрмен ойынның ойыналуының әрбір жағдайы ойын партиясы деп аталады.

Таңдалған және іске асырылған ережемен қарастырылған әрекеттер ойыншының жүрісі деп аталады. Қадамдар жеке және кездейсоқ болу мүмкін. Жеке қадам-бұл ойыншының мүмкін әрекеттерден біреуін саналы таңдауы (мысалы, шахмат ойынында). Кездейсоқ жүріс –бұл ойыншының кездейсоқ таңдалған әрекеті (мысалы, араластырылған карттардың ішінен карт таңдау күмісті лақтыру арқылы).

Ойындар теориясының мақсаты әрбір ойыншы үшін тиімді стратегияны анықтау болып табылады.

Ойындарды топтастыру

Ойынды ойыншылар саны, стратегия саны, ойыншылардың өзараәрекеттестік сипаты, ұтыс сипаты, жүріс саны, ақпараттың жағдайы және т.б. бойынша топтастыруға болады.

1. Ойыншының саныны байланысты ойынды мыналар бойынша айрады:

• қос, егер екі ойыншы қатысса

• көпшілік, егер ойыншының саны екіден көп болса

Олардың біріншіші кең зерттелген. Үш және одан да көп ойыншылардың ойыны шешімді алудың техникалық мүмкіншілігі мен пайда болатын қиыншылықтан аз зерттелген. Ойыншы көп болса – проблемада сондай-ақ көп.

2. Ойынның стратегия саны бойынша:

• соңғы, егер ойыншыда соңғы стратегия саны болса

• шексіз, егер кем дегенде бір ойыншыда мүмкіншілік стратегияның шексіз саны болса.

3. Ойынның өзараәрекеттестік сипаты бойынша:

• коалициондық емес – ойыншылар келісімге өтуге, коалиция құруға рұқсаты жоқ;

• коалициондық (кооперативті) – кооперативті ойындарда коалиция алдын ала аңықталған.

4.Ойын ұтысының сипаты бойынша :

• нөлдік қосынды ойындары (немесе антагонистикалық) – ойыншылардың жалпы капиталы өзгермейді, ол ойыншылар арасында бөлінеді, барлық ойыншылардың ұтыс қосындысы нөлге тең (яғни бір ойыншының ұтысы басқа ойыншының ұтылымына тең)

• нөлдік емес қосынды ойындары.

5.Ұтыстың функцияларының түрі бойынша ойындар матрицалық, биматрицалық, үздіксіз, дөнес, сепарабельді, дуэль түрлеріне бөлінеді және т.б..

• Матрицалық ойын – бұл екі ойыншының нөлдік қосындысы бар соңғы ойыны, онда 1 ойыншының ұтысы матрица түрінде беріледі (матрица қатары 2 ойыншының қолданылатын стратегиясының нөміріне сәйкес келеді, бағанасы – 2 ойыншының қолданылатын стратегиясының нөміріне; матрицаның қатар мен бағана қиылысында қолданылатын стратегияларға сәйкес 1 ойыншының ұтысы жатады). Матрицалық ойындар үшін мына дәлелденді: кез келгенде шешімі бар және ол сызықтық программалау есебіне келтіру арқылы оңай табылады.

• Биматрицалық ойындар – бұл екі ойыншының нөлдік емес қосындысы бар соңғы ойыны, онда әрбір ойыншының ұтысы матрица түрінде сәйкес ойындар үшін жеке беріледі (әрбір матрицада қатар 1 ойыншының стратегиясына сәйкес келеді , бағанасы – 2 ойыншының стратегиясына, бірінші матрицаның қатар мен бағана қиылысында 1 ойыншының ұтысы жатыр, ал екінші матрицада- 2 ойыншының ұтысы). Биматрицалық ойындар үшін ойыншылардың тиімді тәртібінің теориясы өнделген , бірақта мұндай түрдегі ойындарды матрицалық ойындарға қарағанда шешуге қиындырақ.

• Үздіксіз деп әрбір ойыншы үшін ұтыс функциясы стратегияға байланысты үздіксіз болып табылатын ойынды есептейді. Бұл кластағы ойындарда шешімі бар екені дәлелденді, бірақта оларды табудың тиімді тәсілдері табылған жоқ.

• Дөнес деп егер ұтыс функциясы дөнес болып табылатын ойынды есептейді. Оларды шешу үшін бір ойыншы үшін таза тиімді стратегияны табудан тұратын тиімді тәсілдер өнделген. Мұндай есеп оңай шешіледі.

Ойын стратегиясы. Нөлдік қосындысы және нөлдік емес қосындысы ойындары.

Ойыншының стратегиясы деп пайда болған жағдайға байланысты әрбір жеке жүрісі кезінде оның іс әрекеттерінің таңдауынy аңытайтын ережелер жиынтығы. Әдетте, ойыншы ойын процессінде жеке жүріс кезінде қалыптасқан жағдайға байланысты таңдауын жасайды. Бірақ, ойыншының алдын ала шешім қабылдауы да мүмкін. Бұл ойыншының өзіне кесте түрінде берілген немесе программа түрінде анық бір стратегияны тандағанын білдіреді.

Егер ойын жеке жүрістерден тұратын болса, онда ойынның шығысы аңықталған, егер әрбір ойыншы өз стратегиясын таңдаса. Бірақта егер ойында кездесойық жүрістер болса, онда ойын ықтималдық ситатта болады және ойыншылардығ таңдау стратегиясы әлі ойынның шығысы аңықтамайды.

Ойынды шешу үшін немесе ойынның шешімін табу үшін әрбір ойыншы үшін тиімділік шартын қанағаттандыратын стратегияны таңдау керек, яғни екіншісі өз стратегиясына ұсталынған кезде ойыншының біреуі максималды ұтыс алуы керек. Сол уақытта екінші ойыншы минималды ұтылымы болу керек, бірінші өз стратегиясын қолданғанда. Ондай стратегияларды тиімді деп атайды.

Ойын ұтысының сипаты бойынша :

• нөлдік қосынды ойындары (немесе антагонистикалық) – ойыншылардың жалпы капиталы өзгермейді, ол ойыншылар арасында бөлінеді, барлық ойыншылардың ұтыс қосындысы нөлге тең (яғни бір ойыншының ұтысы басқа ойыншының ұтылымына тең)

• нөлдік емес қосынды ойындары.

Төлем матрицасы. Ұтып алу матрицасы.

Қос соңғы ойынды қарастырайық.

А ойыншыда m А_1, А₂, …, А_m жеке стратегиялары болсын

В ойыншыда n B₁, B₂, …, B_n жеке стратегиялары болсын

Онда ойынның m x n өлшемі бар деп айтады.

Ойыншылардың кез келген A_i және B_j (i=1,2,…,m; j=1,2,..n) қос стратегияларын таңдау нәтижесінде ойынның шығысы анықталады, яғни А ойыншының ұтысы және В.ойыншының ( ) ұтылымы

(A_i, B_j) кез келген қос стратегиялар үшін мәндері белгілі деп болжайық. матрицасы элементтері. Элементтері A_i және B_j стратегияларына сәйкес келетін Р( ) матрицасының ұтысы төлем матрицасы немесе ойынның матрицасы деп аталады. Мұндай түрдегі матрицаның жалпы түрі кестеде көрсетілген.

 

Bj Ai	B1	B2	…	Bn
A1			…
A2			…
…	…	…	…	…
Am			…

А_1, А₂, …, А_m.стратегиялар арасында ең жақсысың аңықтайық

A_i стратегиясын таңдай отыра, А ойыншы В ойыншы B_j стратегиясынан жауап береді деп есептеу керек, А ойыншы үшін ұтыс аз . В ойыншының барлық мүмкіншілік стратегиялары үшін A_i стратегиясын таңдау кезінде А ойыншының ең аз ұтысы :

Барлық сандар (i=1,2, …, m) арасынан ең үлкенін таңдаймыз:

- ойынның төменгі бағасы немесе максималды ұтыс (максимин) деп атайды Бұл B ойыншының кез келген стратегиясы кезінде А ойыншының кепілдік ұтысы .

Сондықтан,

Максиминге сәйкес келетін стратегияны максимин стратегиясы деп аталады.

В ойыншы А ойыншының ұтысын азайтуға қызығуда; B_j стратегиясын таңдай отыра ол А үшін максималды мүмкіншілікті ескереді. Белгілейік

Барлық сандар арасында ең кішісін табамыз .

- ойынның жоғағарғы бағасы деп атайды немесе минималды ұтыс (минимакс). Бұл В ойыншы үшін кепілдік ұтылымы. Минимаксқа сәйкес келетін стратегия минимаксті стратегиясы деп аталады.

 

Мысал 1. "Іздеу" ойыны.

А ойыншы екі баспананың біріеуінде тығылып қалу мүмкін (I және II); B ойыншы А ойыншыны іздейді, және егер тапсы , онда А ойыншыдан 1 ақша бірлігімен айыппұл алады, керсінше жағдайда А ойыншыға 1 ақша бірлігін төлейді. Ойынның төлем матрицасын құрып,, ойынның төменгі және жоғарғы бағасы мен сәйкес стратегияларын аңықтаңыз.

шешімі.

А ойыншы I баспанада тығылып қалуы мүмкін - бұл стратегияны А₁ арқылы белгілейміз немесе II баспанада - А₂ стратегиясы. В ойыншы бірініші ойыншыны I баспанада іздеуі мүмкін - В₁ стратегиясы, немесе II баспанадан - В₂ стратегиясы.

Егер А ойыншы I баспанада болса және оны одан В ойыншы тауып алса, онда қос стратегия (А₁,В₁) іске асырылады, А ойыншы айыппұл төлейді, яғни . Соған сәйкес (А₂,В₂) деп аламыз. (А₁,В₂) және (А₂,В₁) стратегиялары А ойыншыға 1 ұтысты береді , сондықтан .Сөйтіп төлем матрицасын аламыз

А₁ стратегиясын таңдау кезінде минималды ұтысы тен және В ойыншының стратегиясына сәйкес келеді. А₂ стратегиясын таңдау кезінде минималды ұтысы тең, ол В₂ стратегия кезінде пайда болады.

В ойыншының кез стратегиясы кезінде өзіне максималды ұтысқа кепілдік бере отыра, яғни ойынның төменгі бағасын , А ойыншы кез келген стратегияны таңдай алады: А₁ немесе А₂, яғни кез келген оның стратегиясы максимин болып табылады.

В₁ (1 бағана) таңдай отыра, В ойыншы А ойыншы өз ұтысын көбейту үшін А₂ стратегиясымен жауап беретінін түсінеді.. Сондықтан, В₁ стратегиясын таңдау кезінде В ойыншының максималды ұтылымы тең.

Осыған сәйкес В₂ стратегиясын таңдау кезінде (столбец 2) В ойыншының максималды ұтылымы тең.

Сөйтіп, А ойыншының кез келген стратегиясы кезінде В ойыншының кепілдік минималды ұтылымы тең- ойынның жоғары бағасына.

В ойыншының кез келген стратегиясы минимаксты болып табылады.

 

Bj Ai	B1	B2
А1	-1	1	-1
А2	1	-1	-1
	1	1

Бұл мысалда ойынның төменгі және жоғарғы бағасы әртүрлі: .

 

Егер ойынның жоғарғы және төменгі бағасы сәйкес келсе, онда ойынның төменгі және жоғарғы бағасының жалпы мәні ойынның таза бағасы деп аталады немесе ойынның бағасы. Ойынның бағасына сәйкес келетін минимаксты стратегиялары тиімді стратегиялары, ал олардың жиынтығы - тиімді шешімі немесе ойынның шешімі болып табылады. Бұл жағдайда А ойыншы максималды кепілдік ұтысты алады, ал В ойыншы минималды кепілдік ұтылымды талап етеді.

Ойын шешімі тұрақтылыққа ие деп айтады, яғни егер ойыншының біреуі өзінің тиімді стратегиясына ұсталынса, онда басқасы үшін өзінің тиімді стратегиясынан бас тартуға пайдалы емес.

A_i және B_j қос таза стратегиялар ойынның тиімді шешімін береді тек және тек мына жағдайда ғана , егер оған сәйкес келетін элементі біруақытта өз бағанасында ең үлкен және қатарында ең кіші болса. Мұндай жағдай бар болса қайқы ер нүктесі деп аталады.

Мысал 2. Төлем матрицасымен берілген ойынның төменгі және жоғарғы бағасын анықтаңыз.

 

Ойынның қайқы ер нүктесі бар ма?

Шешім.

Матрицаның қатарларын талдай отыра ( А ойыншының стратегиясы), бағанасын толтырамыз . осыған сәйкес.

 

	В1	В2	В3
А1	0,5	0,6	0,8	0,5
А2	0,9	0,7	0,8	0,7
А3	0,7	0,6	0,6	0,6
	0,9	0,7	0,8

 

Ойынның төменгі бағасы және ойынның жоғарғы бағасы . Бұл мәндер тең, яғни , және қос стратегияның бірінде (А₂,В₂) жетеді. Сондықтан, ойынның қайқы ер нүктесі (А₂, В₂) және ойынның бағасы .

Дәріс 12. Тақырып: Модельдің ұғымы және модельді сипаттау тәсілдері.

Модельдің ұғымы және модельді сипаттау тәсілдері. Регрессионды модельдер.

XX ғасырда модель түсінігі нақты және идеалдык модельдерді қатар камтитындай болып жалпыланды. Абстрактылы модель түсінігі математикалык модельдер щенберінен шығып, әлем туралы білімдер мен танымдардың барлығына катысты болды. Модель түсінігінін айналасындағы кең талқылаудың қазіргі кезде де жалғасып отырғандығын естен шыгармау қажет. Бастапқыда акпараттык, кибернетикалық бағыттардағы ғылыми пәндер аясында, содан соң ғылымның басқа да салаларында түрлі тәсілдермен іске асырылатын модель ретінде танылды. Негізінде модель білімнің мәнін нақтылау тәсілі ретінде карастырылады.

Модель - 1) касиеттері белгілі бір мағынадағы жүйенін немесе процестің касиеттеріне ұқсас объектілер немесе процестер жүйесі; 2) сериялы бұйымдарды жаппай ендіруге арналған үлгі, эталон; кез-келген бір объекті жұмысы, мыс, процессордын жұмыс істеуін модельдейтін программа немесс кұрылғы. Ол материалдық объект түрінде, математикалық байланыстар жүйесі ретінде немесе құрылымды имитациялайтын программа күйінде құрастырылады да, қарастырылатын объектінің жұмыс істеуін зерттеу үшін қолданылады. Модельге қойылатын негізгі талап - оның қасиеттерінің негізгі объектіге сейкес келуі, яғни барабарлығы.

Модельдеу - кез-келген құбылыстардың, процестердің немесе объект жүйелерінің қасиеттері мен сипаттамаларын зерттеу үшін олардын үлгісін күру (жасау) және талдау; бар немесе жаңадан кұрастырьшған объектілердің сипатын аныктау немесе айқындау үшін олардың аналогтарында (моделінде) объектілердің әр түрлі табиғатын зерттеу әдісі.

Модель төрт деңгейде түпнұсканың гносеологиялық орынбасары бола алады: 1-элементтер деңгейінде, 2-кұрылым дейгейінде, 3- қалып-күй немесе қызметтік денгейін, 4-нәтижелер дейгейінде. Сипаты бойынша модельдеу материалдык және идеалдық болып бөлінеді. Материалдык модельдеу объектінің геометриялық, физикалық, динамикалық және кызметтік сипатын нақты дәл береді. Идеалдык модельдеуге объектінің ойдағы бейнесі жатады. Ойша модельдеу тіл көмегімен іске асырылады.

"Модель" түсінігі кибернетикада бакыланатын объектілер класын сипаттайтын теорияның моделін белгілеуде жиі қолданылады. Демек, кибернетикада берілген нақты объектінің моделі осы объект туралы теорияның моделі болып табылады. Компьютерлік модельдеу - бұл да оқып үйренетін объекті теориясының модельденуі.

Модельдеуші (модель субъектісі) тек адам бола алады. Модельдеу объектісі табиги (өсімдік, күн системасы) және адамның ыклалымен қүрылып жасанды болуы мүмкін (1-сурет).