
Образец выполнения
Задача 1.
Даны координаты точек
![]() .Требуется:
.Требуется:
Найти координаты векторов .
Найти вектор , если .
Выяснить, будут ли векторы и перпендикулярны.
Найти вектор выяснить, будут ли векторы и коллинеарны.
Решение:
1. Чтобы найти
координаты вектора
![]() ,
заданного координатами начала и конца
,
заданного координатами начала и конца
![]() ,
необходимо из координат конца вектора
вычесть координаты начала, то есть
,
необходимо из координат конца вектора
вычесть координаты начала, то есть
![]() .
В нашем случае
.
В нашем случае
![]() ,
,
![]()
![]()
2. Если векторы
перпендикулярны, то их скалярное
произведение равно нулю, то есть
![]() .
Длина вектора, заданного своими
координатами, вычисляется по формуле:
.
Длина вектора, заданного своими
координатами, вычисляется по формуле:
![]() .
.
Пусть искомый
вектор имеет координаты
![]() .
Так как
,
то
.
Так как
,
то
![]() ,
,
![]() и
и
![]() .
Составим из полученных равенств систему:
.
Составим из полученных равенств систему:

Из последнего
уравнения системы находим
![]() ,
подставляя в первые два уравнения
системы получаем:
,
подставляя в первые два уравнения
системы получаем:
![]() и
и
![]()
3. Найдем скалярное произведение векторов и .
![]() ;
;
![]() .
.
Следовательно,
векторы
![]() и
и
![]() .
.
4. Векторным
произведением векторов
![]() называется
вектор
,
координаты которого в ортонормированном
базисе
называется
вектор
,
координаты которого в ортонормированном
базисе
![]() можно вычислить следующим образом:
можно вычислить следующим образом:

Векторы коллинеарны,
если их координаты пропорциональны:
![]()
В нашем случае имеем:

![]() Итак,
Итак,
![]()
Составим отношение
координат векторов
и
![]() :
:
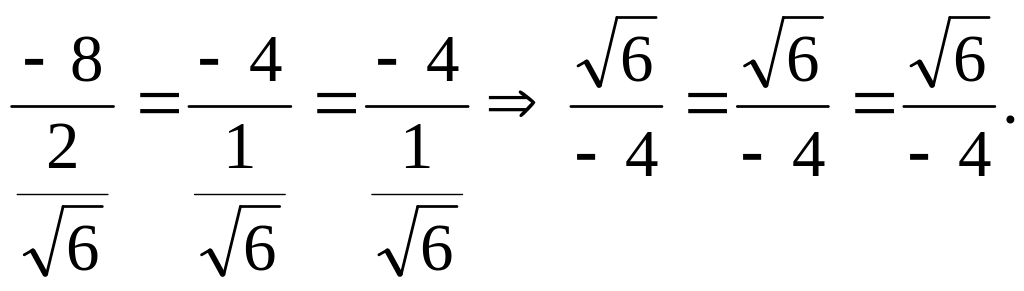
Составим отношение
координат векторов
и
![]() :
:

Следовательно, векторы и коллинеарны и векторы и коллинеарны.
Ответ:
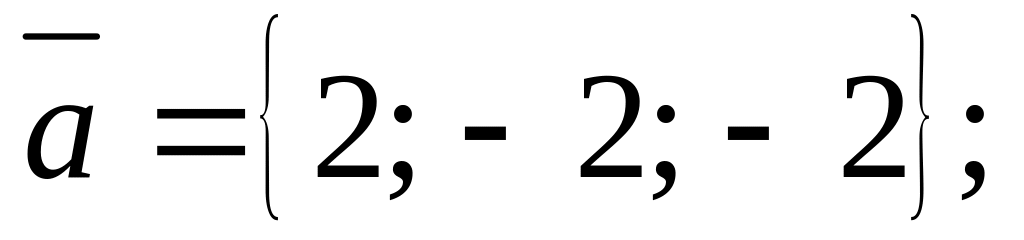


 .
.
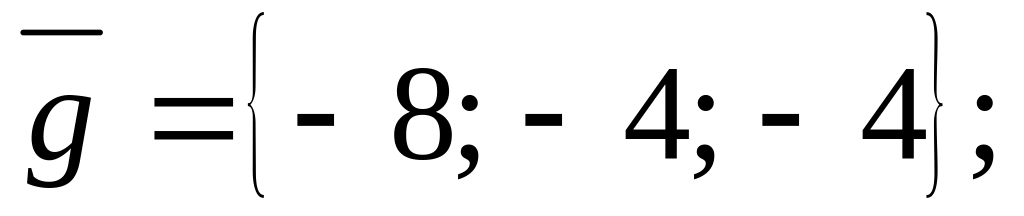 и
коллинеарны.
и
коллинеарны.
Задача 2.
Дан треугольник
АВС,
в котором
![]() ,
точки
- середины сторон треугольника, лежащие
напротив соответствующих вершин, О
– точка пересечения медиан. Выразить
векторы
,
точки
- середины сторон треугольника, лежащие
напротив соответствующих вершин, О
– точка пересечения медиан. Выразить
векторы
![]() через векторы
и
,
указать их координаты в этом базисе.
через векторы
и
,
указать их координаты в этом базисе.
Решение:
Неколлинеарные векторы
![]() и
и
![]() образуют
базис пространства
образуют
базис пространства
![]() ,
следовательно, любой вектор этого
пространства можно разложить по базисным
векторам, т. е. представить в виде
комбинации базисных векторов. Коэффициенты
этого разложения будут являться
координатами вектора в указанном базисе.
,
следовательно, любой вектор этого
пространства можно разложить по базисным
векторам, т. е. представить в виде
комбинации базисных векторов. Коэффициенты
этого разложения будут являться
координатами вектора в указанном базисе.

При решении задачи используем свойство медиан треугольника: медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины (рис.1), т. е.
![]() и т.п.
и т.п.
рис. 1
Середины сторон треугольника – точки делят стороны пополам.
Используя правила сложения векторов выразим искомые векторы и укажем их координаты в данном базисе. Итак, имеем:
![]() то есть
то есть
![]()
![]() то есть
то есть
![]()
![]()
![]() то есть
то есть
![]()
Замечание:
Если в задаче задан правильный шестиугольник, то используют тот факт, что в нем имеется три пары параллельных сторон (каждая из пар параллельна одной из диагоналей), их можно выразить коллинеарными векторами.
Если в задаче задана равнобокая трапеция, то в ней имеется пара подобных треугольников, основания которых совпадают с основаниями трапеции, а две другие в сумме составляют диагонали. При заданном соотношении между основаниями (равном коэффициенту подобия) легко выражаются отрезки диагоналей трапеции.
Ответ:
Задача 3.
Даны четыре вектора
![]() .
Построить из данных векторов базис и
выразить в нем небазисный вектор.
.
Построить из данных векторов базис и
выразить в нем небазисный вектор.
Решение: известно,
что любые три некомпланарных вектора
образуют базис пространства
![]() ,
и любой четвертый вектор единственным
образом разлагается по базису. Признак
компланарности векторов: смешанное
произведение равно нулю.
,
и любой четвертый вектор единственным
образом разлагается по базису. Признак
компланарности векторов: смешанное
произведение равно нулю.
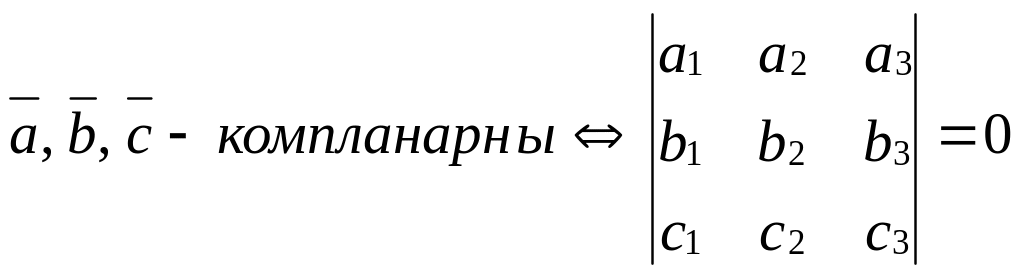 .
.
Найдем смешанные произведения, вычислив определители разложением по строке или столбцу:

![]()

![]()
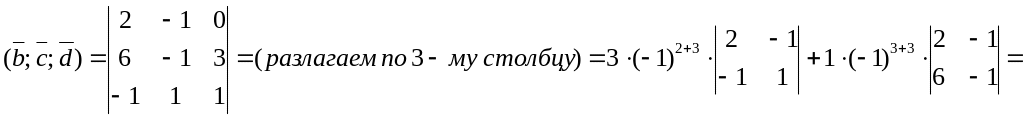
![]()

![]()
Следовательно,
любая из троек векторов образует базис
пространства
![]()
Рассмотрим в
качестве базиса, например, систему
векторов
![]() ,
а вектор
разложим по этому базису в виде
,
а вектор
разложим по этому базису в виде
![]() ,
где
,
где
![]() -
координаты вектора
в
базисе
.
-
координаты вектора
в
базисе
.
![]()
![]()
![]()
Равенство векторов означает равенство соответствующих координат этих векторов.
Получим систему:
 Решая эту систему
любым из методов (например, Крамера или
Гаусса), найдем новые координаты вектора
в
базисе
.
Решая эту систему
любым из методов (например, Крамера или
Гаусса), найдем новые координаты вектора
в
базисе
.
Определитель
 .
Так как определитель
.
Так как определитель
![]() основной
матрицы системы уравнений отличен от
нуля, значит, по теореме Крамера данная
система имеет единственное решение,
которое можно найти, например, по формулам
Крамера:
основной
матрицы системы уравнений отличен от
нуля, значит, по теореме Крамера данная
система имеет единственное решение,
которое можно найти, например, по формулам
Крамера:
![]()
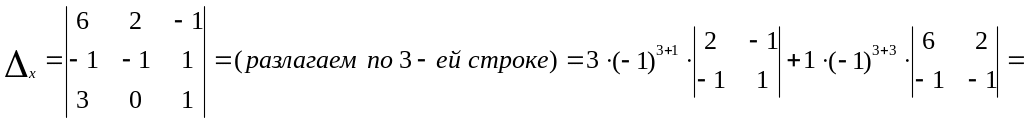
![]()
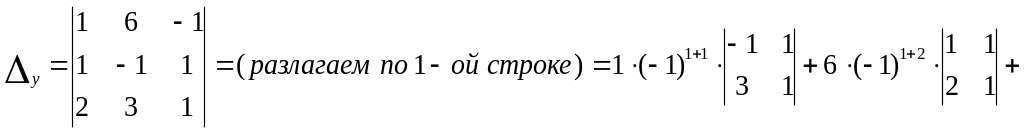
![]()

![]()
![]()
Итак, вектор
![]() -
искомое разложение вектора
в базисе
.
-
искомое разложение вектора
в базисе
.
Ответ: .
Задача 4. Даны
координаты вершин пирамиды
:
![]() .
Средствами векторной алгебры найти:
.
Средствами векторной алгебры найти:
угол между ребрами и ;
площадь грани ;
точку пересечения медиан треугольника , используя формулы координат точки, делящей отрезок в данном отношении;
объем пирамиды;
длину высоты, опущенной из вершины на грань .
Решение:
1 .Угол
между ребрами
и
равен
углу между векторами
.Угол
между ребрами
и
равен
углу между векторами![]() и
и
![]() (рис.2), этот угол вычисляется по формуле:
(рис.2), этот угол вычисляется по формуле:
![]()
Найдем координаты векторов и .
![]()
рис.2
![]()
![]()
![]()
Найдем скалярное
произведение:
![]()
Итак,
![]() т.е.
т.е.
![]()
2. Площадь S
грани
найдем,
используя геометрический смысл векторного
произведения:
![]() где
где
![]()

![]()
Итак,
![]()
3 .
Найдем точку пересечения медиан
треугольника
.
.
Найдем точку пересечения медиан
треугольника
.
Рассмотрим одну
из медиан (рис.3), например, медиану
![]()
![]() - середина стороны
- середина стороны
![]() Используем
формулы координат середины отрезка:
Используем
формулы координат середины отрезка:
![]()
рис.3
где
![]()
![]()
![]()
Известно, что в
треугольнике медианы пересекаются в
одной точке и делятся ею в отношении
2:1, считая от вершины. Точку пересечения
медиан треугольника
![]() найдем, используя формулы координат
точки, делящей направленный отрезок
(вектор
найдем, используя формулы координат
точки, делящей направленный отрезок
(вектор
![]() )
в данном отношении:
)
в данном отношении:
![]()
Итак,

4. Объем V пирамиды найдем, используя геометрический смысл смешанного произведения векторов, совпадающих с ребрами пирамиды:
![]() где
где
![]()
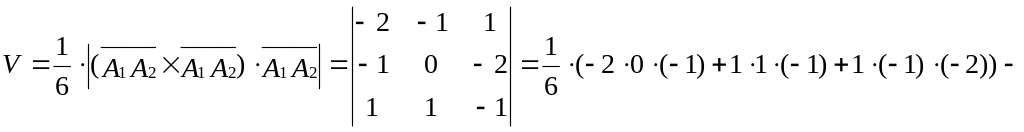
![]()
![]()
![]()
5. Длину высоты, опущенной из вершины на грань , можно найти
![]() .
.

Ответ:
1.
![]()
2.
![]()
3.
![]() -
точка пересечения медиан;
-
точка пересечения медиан;
4.
![]()
5.
![]()
