Индивидуальное домашнее задание № 2 Тема: Векторная алгебра
Индивидуальное домашнее задание № 2 состоит из четырех задач, для каждой из которых приведено 30 вариантов. Номер варианта, сроки выполнения и защиты типового расчета устанавливаются преподавателем, ведущим в группе практические занятия, в соответствии с учебным планом.
Решению задач должно предшествовать условие, которое формулируется применительно к варианту, по которому работает студент.
При защите работы студент должен уметь отвечать на теоретические вопросы, объяснять решение каждой задачи своего варианта и решать подобные задачи.
Теоретические вопросы
Понятие вектора, сонаправленные, противоположно направленные векторы.
Длина вектора, нулевой вектор, единичный вектор.
Коллинеарные векторы. Признак коллинеарности векторов.
Равные, противоположные векторы.
Компланарные векторы. Признак компланарности векторов.
Сложение векторов (правило треугольника, параллелограмма, многоугольника). Разность векторов.
Умножение вектора на число.
Свойства линейных операций с векторами.
Проекция вектора на ось.
Линейная зависимость и линейная независимость векторов.
Свойства линейной независимости векторов.
Базис и размерность линейного векторного пространства.
Разложение вектора пространства через базисные векторы.
Разложение вектора по ортам координатных осей.
Координаты и модуль вектора, заданного координатами начала и конца.
Направляющие косинусы вектора.
Действия над векторами, заданными своими координатами (линейные операции, равенство, коллинеарность).
Скалярное произведение и его свойства.
Выражение скалярного произведения через координаты.
Угол между векторами.
Признак перпендикулярности векторов.
Векторное произведение векторов и его свойства.
Выражение векторного произведения через координаты.
Геометрические приложения векторного произведения.
Смешанное произведение векторов и его свойства.
Выражение смешанного произведения через координаты.
Геометрические приложения смешанного произведения.
Типовые задачи
Задача 1.
Даны координаты точек
.Требуется:
Найти координаты векторов
.Найти вектор
,
если
.Выяснить, будут ли векторы
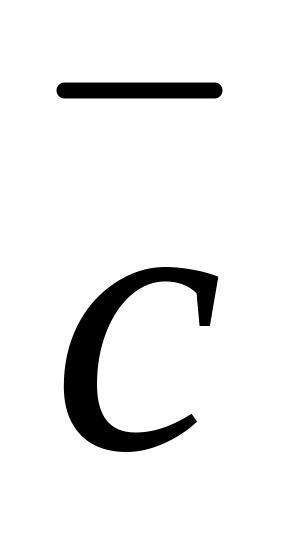и
перпендикулярны.Найти вектор
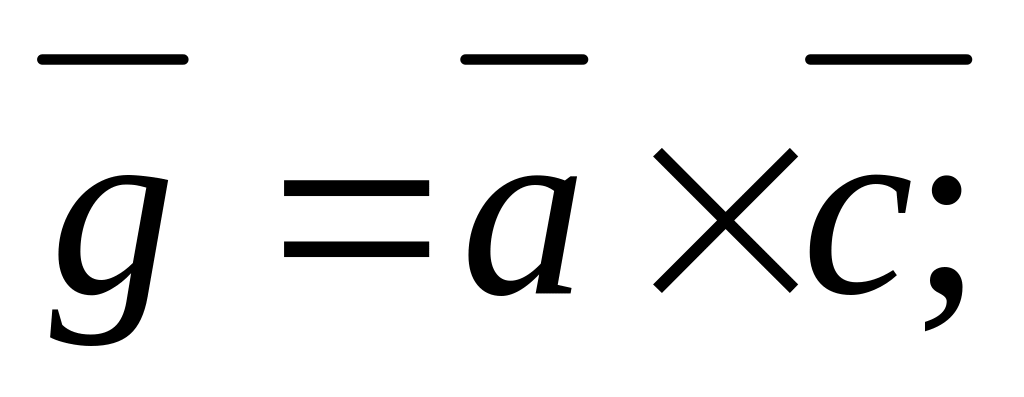выяснить, будут ли векторы
и
коллинеарны.
№ |
А |
В |
С |
1 |
(2;-3;1) |
(-3;2;2) |
(0;-1;-2) |
2 |
(1;-2;1) |
(2;1;2) |
(-2;-1;3) |
3 |
(3;1;-1) |
(-2;2;0) |
(1;-2;2) |
4 |
(-2;0;2) |
(3;-2;-1) |
(1;1;3) |
5 |
(0;-1;-2) |
(-2;3;1) |
(3;-2;2) |
6 |
(2;3;-1) |
(3;-2;2) |
(0;1;-2) |
7 |
(0;2;-1) |
(-2;3;2) |
(1;-2;1) |
8 |
(2;0;-2) |
(-2;2;1) |
(1;-1;3) |
9 |
(2;2;2) |
(1;-3;-2) |
(-1;-1;2) |
10 |
(-3;1;2) |
(2;2;-3) |
(-1;-2;0) |
11 |
(2;-1;1) |
(2;2;-2) |
(-2;1;3) |
12 |
(-2;1;1) |
(1;2;2) |
(-1;-2;3) |
13 |
(-1;0;-2) |
(-2;3;2) |
(1;0;-2) |
14 |
(-2;0;2) |
(3;-1;1) |
(1;2;-2) |
15 |
(-1;2;2) |
(3;1;0) |
(2;-2;1) |
16 |
(1;1;-2) |
(2;2;1) |
(-2;3;-1) |
17 |
(2;-1;0) |
(3;2;-2) |
(-2;1;1) |
18 |
(1;-3;0) |
(-2;-2;1) |
(-2;-1;2) |
19 |
(-3;-2;1) |
(-1;2;-1) |
(2;2;2) |
20 |
(1;2;-3) |
(2;-3;2) |
(-2;0;-1) |
21 |
(-2;-1;3) |
(1;3;1) |
(0;2;-2) |
22 |
(1;3;1) |
(3;-1;-2) |
(-2;2;0) |
23 |
(1;0;3) |
(-2;1;2) |
(2;2;-1) |
24 |
(2;0;-2) |
(-3;2;1) |
(-1;-1;-3) |
25 |
(-2;2;1) |
(1;3;0) |
(2;-1;2) |
26 |
(2;0;1) |
(0;2;3) |
(1;3;0) |
27 |
(-2;1;0) |
(2;-1;-1) |
(-3;-2;2) |
28 |
(0;3;-2) |
(1;0;-3) |
(2;1;0) |
29 |
(2;-1;-1) |
(-2;-3;1) |
(2;2;2) |
30 |
(2;1;-3) |
(-3;2;2) |
(0;-2;-1) |
№ |
А |
В |
С |