
- •Вища та прикладна математика
- •Методичні рекомендації щодо роботи з опорним конспектом лекцій
- •Тема 1. Системи лінійних рівнянь. Метод гауса План:
- •Поняття про системи лінійних рівнянь. Сумісні і несумісні системи рівнянь. Визначені і невизначені системи рівнянь
- •1.2. Розв'язування системи лінійних рівнянь методом послідовного виключення невідомих (метод Гауса)
- •Питання для самоконтролю:
- •Тема 2. Визначники, їх властивості. Правило крамера План:
- •2.1. Визначники другого і третього порядків. Визначники п- го порядку
- •Тема 3. Матриці. Дії з матрицями План:
- •3.1. Матриці. Види матриць. Елементарні перетворення матриці
- •3.2. Ранг матриці. Теорема Кронекера-Капеллі
- •3.3. Множення матриць. Додавання матриць. Множення матриць на число
- •3.5. Застосування матричної алгебри в економіці
- •Питання для самоконтролю:
- •Тема 4. Вектори, лінійні операції над векторами. Скалярний, векторний та мішаний добутки План:
- •Скалярні та векторні величини. Вектори, лінійні операції над ними. Лінійна залежність векторів. Умови колінеарності та компланарності векторів
- •Визначення положення точки радіусом-вектором. Координати на прямій. Координати на площині. Координати у просторі
- •Координати точки поділу. Координати вектора, що заданий двома точками. Ознака колінерності двох векторів. Ознака компланарності трьох векторів
- •Координати середини відрізка :
- •Скалярний, векторний добутки двох векторів, мішаний добуток трьох векторів та їх властивості
- •Питання для самоконтролю:
- •Тема 5. Пряма на площині План:
- •Пряма як лінія першого порядку. Загальне рівняння
- •Рівняння прямої у відрізках на осях. Параметричні і канонічні рівняння прямої. Рівняння прямої, що проходить через дві задані точки. Рівняння прямої з кутовим коефіцієнтом
- •Рівняння прямої, що проходить через дві задані точки:
- •Параметричні рівняння прямої:
- •Рівняння прямої у відрізках на осях:
- •Кут між двома прямими. Умови перпендикулярності і паралельності двох прямих
- •Нормальне рівняння прямої. Відстань точки від прямої Питання для самоконтролю:
- •Тема 6. Графічний метод розвязування задач лінійного програмування План:
- •Основи лінійного опуклого програмування
- •Загальна економіко-математична модель задачі лінійного програмування (злп)
- •Основні поняття
- •Форми запису задач лінійного програмування
- •Побудова опуклості допустимих розв’язків
- •Пошук оптимального плану Алгоритм пошуку оптимального плану злп графічним методом
- •При розв’язуванні злп можливі такі випадки:
- •Питання для самоконтролю:
- •Тема 7. Симплекс-метод знаходження розв'язку основної задачі лінійного програмування План:
- •7.1. Початковий опорний план
- •7.2. Перехід від одного опорного плану до іншого
- •7.3. Оптимальний розв’язок. Критерій оптимальності плану
- •7.4. Розв’язування задачі лінійного програмування симплексним методом Алгоритм розв’язування
- •Питання для самоконтролю:
- •Тема 8. Спряженість у лінійному програмуванні (двоїстість)
- •8.1. Економічна інтерпретація прямої та двоїстої задач лінійного програмування
- •8.2. Правила побудови двоїстих задач
- •8.3. Основні теореми двоїстості та їх економічний зміст
- •Теорема (друга теорема двоїстості для симетричних задач)
- •4. Приклад побудови двоїстої задачі
- •Питання для самоконтролю:
- •Тема 9. Транспортна задача План:
- •9.1. Транспортна задача, як задача лінійного програмування. Постановка транспортної задачі за критерієм мінімальних витрат на перевезення.
- •9.2. Необхідна і достатня умови існування розв’язку транспортної задачі. Знаходження опорного розв’язку задачі методом північно-західного кута та методом мінімального елемента.
- •Метод потенціалів. Потенціальність – ознака оптимальності плану перевезень.
- •Алгоритм методу потенціалів:
- •Визначення типу транспортної задачі (відкрита чи закрита). За необхідності слід звести задачу до закритого типу.
- •Побудова першого опорного плану транспортної задачі одним із методів.
- •Перевірка опорного плану задачі на виродженість. За необхідності вводять нульові постачання.
- •Перевірка плану транспортної задачі на оптимальність.
- •Питання для самоконтролю:
- •Тема 10. Теорія границь. Неперервність функції План:
- •10.1. Поняття про функцію. Область визначення функції. Способи задання функції. Властивості функції
- •Нескінченно малі і нескінченно великі величини, зв'язок між ними
- •Питання для самоконтролю:
- •Тема 11. Похідна функції однієї змінної План:
- •11.1. Означення похідної. Геометричний та механічний зміст похідної. Зв’язок між неперервністю та диференційованістю функції
- •11.2. Похідна складної функції. Основні правила диференціювання. Таблиця похідних елементарних функцій
- •11.3. Похідна оберненої функції. Похідна неявної, степенево-показникової та параметричної функцій. Похідні вищих порядків
- •Питання для самоконтролю:
- •Тема 12. Диференціал функції однієї змінної
- •Тема 13. Основні теореми диференціального числення
- •Правило Лопіталля. Формула Тейлора
- •Питання для самоконтролю:
- •Тема 14. Дослідження функцій за допомогою похідних План:
- •14.1. Умови зростання і спадання функції. Екстремум функції. Необхідна та достатні умови екстремуму функції. Найбільше та найменше значення функції на проміжку
- •Тема 15. Застосування похідної в економічних розрахунках План:
- •Властивості еластичності функції
- •Питання для самоконтролю:
- •Тема 16. Невизначений інтеграл План:
- •Властивості невизначеного інтеграла. Таблиця інтегралів
- •Тема 17. Визначений інтеграл
- •Тема 18. Наближене обчислення та застосування визначеного інтеграла
- •18.1 Наближене обчислення визначеного інтеграла: формули прямокутників, трапецій, парабол
- •Формула прямокутників
- •Формула трапецій
- •Метод парабол (Сімпсона)
- •18.2 Геометричні застосування визначеного інтеграла: обчислення довжин дуг кривих, об‘ємів та площ поверхонь тіл обертання
- •Розрахунок Об’єму тіла обертання
- •Обчислення довжини дуги плоскою кривої
- •18.3 Поняття про невласні інтеграли та їх обчислення
- •Економічний зміст визначеного інтеграла
- •Питання для самоконтролю:
- •Тема 19. Диференціальні рівняння першого порядку План:
- •Тема 20. Диференціальні рівняння другого порядку План:
- •Основні поняття. Загальний розв’язок та загальний інтеграл диференціального рівняння другого порядку. Частинний розв’язок та частинний інтеграл диференціального рівняння другого порядку
- •Диференціальні рівняння другого порядку, що дозволяють знизити порядок Диференціальні рівняння другого порядку:
- •Лінійні диференціальні рівняння другого порядку
- •Питання для самоконтролю:
- •Тема 21. Числові ряди План:
- •Числовий ряд. Частинні суми ряду. Сума ряду. Збіжні та розбіжні ряди. Геометрична прогресія
- •Ряди з доданими членами. Умова збіжності доданого ряду. Теореми порівняння рядів з додатними членами
- •Достатні ознаки збіжності рядів з додатним членами: д’Аламбера, Коші, інтегральна ознака Маклорена-Коші
- •Знакозмінні ряди. Абсолютна та умовна збіжність знакозмінних рядів. Знакопереміжні ряди. Теорема Лейбниця
- •Питання для самоконтролю:
- •Тема 22. Степеневі ряди План:
- •Степеневі ряди. Теорема Абеля. Радіус та інтервал збіжності степеневого ряду
- •Властивості степеневих рядів
- •Ряди Тейлора та Маклорена
- •Ряд Тейлора:
- •Список рекомендованих джерел
Основи лінійного опуклого програмування
Математична
модель
економічного об’єкту (системи) – це
його спрощений образ поданий у вигляді
сукупності математичних співвідношень
(рівнянь, нерівностей, логічних
співвідношень, графіків тощо).

Загальна економіко-математична модель задачі лінійного програмування (злп)
Цільова
функція
Система
обмежень:

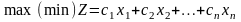 (1)
(1)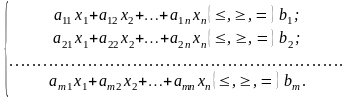 (2)
(2)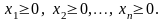 (3)
(3)
Основні поняття
Вектор
Х
= (х1,
х2,
…, хn),
координати якого задовольняють систему
обмежень (2) та умови невід’ємності
змінних (3), називається допустимим
розв’язком (планом) задачі лінійного
програмування.

Допустимий
план Х = (х1, х2, …, хn) називається опорним
планом задачі лінійного програмування,
якщо він задовольняє не менше, ніж m
лінійно незалежних обмежень системи
(2) у вигляді рівностей, а також обмеження
(3) щодо невід’ємності змінних.

Опорний
план

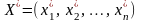 ,
за якого цільова функція (1) досягає
масимального (чи мінімального) значення,
називається оптимальним
розв’язком (планом) задачі лінійного
програмування.
,
за якого цільова функція (1) досягає
масимального (чи мінімального) значення,
називається оптимальним
розв’язком (планом) задачі лінійного
програмування.
Форми запису задач лінійного програмування
max(min)
Z
= CX
за
умов: АХ
= А0; (4)
Х
≥
0,
Векторно-матрична форма:
Де
 матриця коефіцієнтів при змінних;
матриця коефіцієнтів при змінних;
 — вектор
змінних;
— вектор
змінних;
 — вектор вільних членів;
— вектор вільних членів;
С = (с1, с2, …, сп) — вектор коефіцієнтів при змінних у цільовій функції.
max(min)Z
= CX
за
умов:
A1x1
+ A2x2
+ … +
Anxn
= A0; (5)
X
≥0,
Векторна форма:
де
 вектори коефіцієнтів при змінних.
вектори коефіцієнтів при змінних.

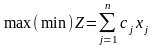
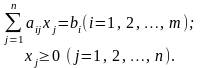 (6)
(6)
Форма у вигляді суми:
Побудова опуклості допустимих розв’язків

Розглянемо на площині х1Оx2 сумісну систему лінійних нерівностей:
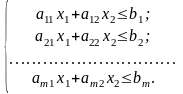

Кожна нерівність системи геометрично визначає півплощину з граничною прямою ai1x1 + ai2x2 = bi (i=1,2, ..., т). Умови невід’ємності змінних визначають півплощини з граничними прямими х1 = 0 та х2 = 0. Система сумісна, тому півплощини, перетинаючись, утворюють спільну частину, що являє собою сукупність точок, координати кожної з яких є розв’язком даної системи.


Сукупність
цих точок (розв’язків) називають
багатокутником
розв’язків,
або областю
допустимих планів (розв’язків) ЗЛП
Пошук оптимального плану Алгоритм пошуку оптимального плану злп графічним методом

1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях задачі знаків нерівностей на знаки рівностей.
2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.
3. Знаходимо багатокутник розв’язків задачі лінійного програмування.
4.
Будуємо напрямний вектор
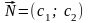 .
.
5.
Будуємо пряму с1х1+с2х2=const,
перпендикулярну до вектора
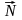 .
.
6.Рухаючи
пряму с1х1+с2х2=const
в напрямку вектора
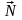 (для задачі максимізації) або в
протилежному напрямі
(для задачі
мінімізації), знаходимо вершину
багатокутника розв’язків, де цільова
функція набирає екстремального значення.
(для задачі максимізації) або в
протилежному напрямі
(для задачі
мінімізації), знаходимо вершину
багатокутника розв’язків, де цільова
функція набирає екстремального значення.
7. Визначаємо координати точки, в якій цільова функція набирає екстремального значення, і обчислюємо його.
