
- •Вища та прикладна математика
- •Методичні рекомендації щодо роботи з опорним конспектом лекцій
- •Тема 1. Системи лінійних рівнянь. Метод гауса План:
- •Поняття про системи лінійних рівнянь. Сумісні і несумісні системи рівнянь. Визначені і невизначені системи рівнянь
- •1.2. Розв'язування системи лінійних рівнянь методом послідовного виключення невідомих (метод Гауса)
- •Питання для самоконтролю:
- •Тема 2. Визначники, їх властивості. Правило крамера План:
- •2.1. Визначники другого і третього порядків. Визначники п- го порядку
- •Тема 3. Матриці. Дії з матрицями План:
- •3.1. Матриці. Види матриць. Елементарні перетворення матриці
- •3.2. Ранг матриці. Теорема Кронекера-Капеллі
- •3.3. Множення матриць. Додавання матриць. Множення матриць на число
- •3.5. Застосування матричної алгебри в економіці
- •Питання для самоконтролю:
- •Тема 4. Вектори, лінійні операції над векторами. Скалярний, векторний та мішаний добутки План:
- •Скалярні та векторні величини. Вектори, лінійні операції над ними. Лінійна залежність векторів. Умови колінеарності та компланарності векторів
- •Визначення положення точки радіусом-вектором. Координати на прямій. Координати на площині. Координати у просторі
- •Координати точки поділу. Координати вектора, що заданий двома точками. Ознака колінерності двох векторів. Ознака компланарності трьох векторів
- •Координати середини відрізка :
- •Скалярний, векторний добутки двох векторів, мішаний добуток трьох векторів та їх властивості
- •Питання для самоконтролю:
- •Тема 5. Пряма на площині План:
- •Пряма як лінія першого порядку. Загальне рівняння
- •Рівняння прямої у відрізках на осях. Параметричні і канонічні рівняння прямої. Рівняння прямої, що проходить через дві задані точки. Рівняння прямої з кутовим коефіцієнтом
- •Рівняння прямої, що проходить через дві задані точки:
- •Параметричні рівняння прямої:
- •Рівняння прямої у відрізках на осях:
- •Кут між двома прямими. Умови перпендикулярності і паралельності двох прямих
- •Нормальне рівняння прямої. Відстань точки від прямої Питання для самоконтролю:
- •Тема 6. Графічний метод розвязування задач лінійного програмування План:
- •Основи лінійного опуклого програмування
- •Загальна економіко-математична модель задачі лінійного програмування (злп)
- •Основні поняття
- •Форми запису задач лінійного програмування
- •Побудова опуклості допустимих розв’язків
- •Пошук оптимального плану Алгоритм пошуку оптимального плану злп графічним методом
- •При розв’язуванні злп можливі такі випадки:
- •Питання для самоконтролю:
- •Тема 7. Симплекс-метод знаходження розв'язку основної задачі лінійного програмування План:
- •7.1. Початковий опорний план
- •7.2. Перехід від одного опорного плану до іншого
- •7.3. Оптимальний розв’язок. Критерій оптимальності плану
- •7.4. Розв’язування задачі лінійного програмування симплексним методом Алгоритм розв’язування
- •Питання для самоконтролю:
- •Тема 8. Спряженість у лінійному програмуванні (двоїстість)
- •8.1. Економічна інтерпретація прямої та двоїстої задач лінійного програмування
- •8.2. Правила побудови двоїстих задач
- •8.3. Основні теореми двоїстості та їх економічний зміст
- •Теорема (друга теорема двоїстості для симетричних задач)
- •4. Приклад побудови двоїстої задачі
- •Питання для самоконтролю:
- •Тема 9. Транспортна задача План:
- •9.1. Транспортна задача, як задача лінійного програмування. Постановка транспортної задачі за критерієм мінімальних витрат на перевезення.
- •9.2. Необхідна і достатня умови існування розв’язку транспортної задачі. Знаходження опорного розв’язку задачі методом північно-західного кута та методом мінімального елемента.
- •Метод потенціалів. Потенціальність – ознака оптимальності плану перевезень.
- •Алгоритм методу потенціалів:
- •Визначення типу транспортної задачі (відкрита чи закрита). За необхідності слід звести задачу до закритого типу.
- •Побудова першого опорного плану транспортної задачі одним із методів.
- •Перевірка опорного плану задачі на виродженість. За необхідності вводять нульові постачання.
- •Перевірка плану транспортної задачі на оптимальність.
- •Питання для самоконтролю:
- •Тема 10. Теорія границь. Неперервність функції План:
- •10.1. Поняття про функцію. Область визначення функції. Способи задання функції. Властивості функції
- •Нескінченно малі і нескінченно великі величини, зв'язок між ними
- •Питання для самоконтролю:
- •Тема 11. Похідна функції однієї змінної План:
- •11.1. Означення похідної. Геометричний та механічний зміст похідної. Зв’язок між неперервністю та диференційованістю функції
- •11.2. Похідна складної функції. Основні правила диференціювання. Таблиця похідних елементарних функцій
- •11.3. Похідна оберненої функції. Похідна неявної, степенево-показникової та параметричної функцій. Похідні вищих порядків
- •Питання для самоконтролю:
- •Тема 12. Диференціал функції однієї змінної
- •Тема 13. Основні теореми диференціального числення
- •Правило Лопіталля. Формула Тейлора
- •Питання для самоконтролю:
- •Тема 14. Дослідження функцій за допомогою похідних План:
- •14.1. Умови зростання і спадання функції. Екстремум функції. Необхідна та достатні умови екстремуму функції. Найбільше та найменше значення функції на проміжку
- •Тема 15. Застосування похідної в економічних розрахунках План:
- •Властивості еластичності функції
- •Питання для самоконтролю:
- •Тема 16. Невизначений інтеграл План:
- •Властивості невизначеного інтеграла. Таблиця інтегралів
- •Тема 17. Визначений інтеграл
- •Тема 18. Наближене обчислення та застосування визначеного інтеграла
- •18.1 Наближене обчислення визначеного інтеграла: формули прямокутників, трапецій, парабол
- •Формула прямокутників
- •Формула трапецій
- •Метод парабол (Сімпсона)
- •18.2 Геометричні застосування визначеного інтеграла: обчислення довжин дуг кривих, об‘ємів та площ поверхонь тіл обертання
- •Розрахунок Об’єму тіла обертання
- •Обчислення довжини дуги плоскою кривої
- •18.3 Поняття про невласні інтеграли та їх обчислення
- •Економічний зміст визначеного інтеграла
- •Питання для самоконтролю:
- •Тема 19. Диференціальні рівняння першого порядку План:
- •Тема 20. Диференціальні рівняння другого порядку План:
- •Основні поняття. Загальний розв’язок та загальний інтеграл диференціального рівняння другого порядку. Частинний розв’язок та частинний інтеграл диференціального рівняння другого порядку
- •Диференціальні рівняння другого порядку, що дозволяють знизити порядок Диференціальні рівняння другого порядку:
- •Лінійні диференціальні рівняння другого порядку
- •Питання для самоконтролю:
- •Тема 21. Числові ряди План:
- •Числовий ряд. Частинні суми ряду. Сума ряду. Збіжні та розбіжні ряди. Геометрична прогресія
- •Ряди з доданими членами. Умова збіжності доданого ряду. Теореми порівняння рядів з додатними членами
- •Достатні ознаки збіжності рядів з додатним членами: д’Аламбера, Коші, інтегральна ознака Маклорена-Коші
- •Знакозмінні ряди. Абсолютна та умовна збіжність знакозмінних рядів. Знакопереміжні ряди. Теорема Лейбниця
- •Питання для самоконтролю:
- •Тема 22. Степеневі ряди План:
- •Степеневі ряди. Теорема Абеля. Радіус та інтервал збіжності степеневого ряду
- •Властивості степеневих рядів
- •Ряди Тейлора та Маклорена
- •Ряд Тейлора:
- •Список рекомендованих джерел
Властивості невизначеного інтеграла. Таблиця інтегралів
Функцію
F(x)
називають первісною
для функції f(x)
на проміжку X,
якщо в усіх точках цього проміжку
функція F(x)
диференційована і виконується рівність
F´(x)=f(x),
або dF(x)=f(x)dx.


Таблиця інтегралів
1.
|
10.
|
2.
|
11.
|
3.
|
12.
|
4.
|
13.
|
5.
|
14.
|
6.
|
15.
|
7.
|
16.
|
8.
|
17.
|
9.
|
18.
|
Приклад
Знайти невизначений інтеграл:
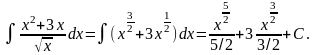
 16.2.
Метод безпосереднього інтегрування.
Заміна змінної (або підстановка) у
невизначеному інтегралі. Інтегрування
частинами
16.2.
Метод безпосереднього інтегрування.
Заміна змінної (або підстановка) у
невизначеному інтегралі. Інтегрування
частинами

Питання для самоконтролю:
Дайте означення первісної функції.
Що називається невизначеним інтегралом.
Охарактеризуйте основні властивості невизначеного інтегралу.
У чому суть безпосереднього інтегрування?
У чому суть заміни змінної у невизначеному інтегралі?
У чому суть інтегрування частинами у невизначеному інтегралі?
Тема 17. Визначений інтеграл
План:
Означення визначеного інтеграла. Формула Ньютона-Лейбниця. Заміна змінної у визначеному інтегралі. Інтегрування частинами визначеного інтеграла.
Невласні інтеграли.
Обчислення площ плоских фігур.
Джерела:6, 15, 22, 27, 31, 34, 35, 40, 50.
Міні-лексикон: визначений інтеграл, формула Ньютона-Лейбниця невласний інтеграл, збіжний та розбіжний інтеграли.
 17.1.
Означення визначеного інтеграла. Формула
Ньютона-Лейбниця. Заміна змінної у
визначеному інтегралі. Інтегрування
частинами визначеного інтеграла
17.1.
Означення визначеного інтеграла. Формула
Ньютона-Лейбниця. Заміна змінної у
визначеному інтегралі. Інтегрування
частинами визначеного інтеграла
Інтегрування
частинами визначеного інтеграла:
Якщо
функції u(x)
таv(x)
неперервно
диференційовані на відрізку [a,b],
тоді:
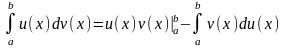 .
.
Приклад
Обчислити
інтеграл
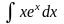
Розв’язання.
Припустивши
 ,
,
 ,
тоді
,
тоді 
Звідси
матимемо .
.
17.2. Невласні інтеграли
Існує
скінчена
границя

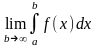 ,
яку
називають
невласним
інтегралом
від
функції
f(x)
в
інтервалі
,
яку
називають
невласним
інтегралом
від
функції
f(x)
в
інтервалі і позначають:
і позначають:
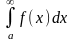 .
.


 17.3.
Обчислення площ плоских фігур
17.3.
Обчислення площ плоских фігур
Питання для самоконтролю:
Що називають визначеним інтегралом?
Запишіть формулу Ньютона-Лейбниця.
У чому суть заміни змінної у визначеному інтегралі?
У чому суть інтегрування частини у визначеному інтегралі?
Що таке інтеграли з нескінченними межами інтегрування?
Що таке інтеграли від необмежених функцій?
Як обчислити площі фігур, використовуючи визначений інтеграл?
Тема 18. Наближене обчислення та застосування визначеного інтеграла
План
18.1. Наближене обчислення визначеного інтеграла: формули прямокутників, трапецій, парабол.
18.2. Геометричні застосування визначеного інтеграла: обчислення довжин дуг кривих, об‘ємів та площ поверхонь тіл обертання.
18.3. Поняття про невласні інтеграли та їх обчислення.
18.4. Деякі застосування інтегрального числення в задачах економіки.
Джерела:6, 15, 22, 27, 31, 34, 35, 40, 50.
Міні-лексикон: інтеграл, площа фігури, наближене обчислення.


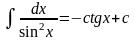


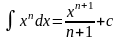 (n≠-1)
(n≠-1)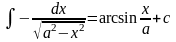
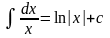




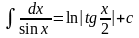
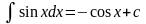
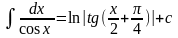
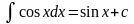
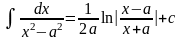
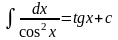
 .
.