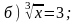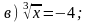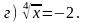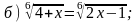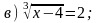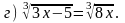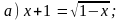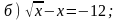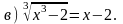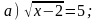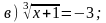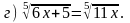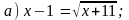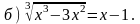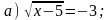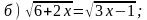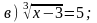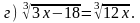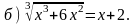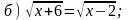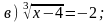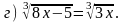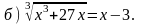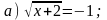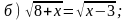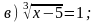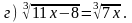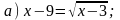- •Содержание
- •Перечень практических работ
- •Практическая работа № 1 Выполнение действий с рациональными числами. Решение рациональных уравнений, неравенств, систем уравнений и неравенств первой степени.
- •Средства обучения:
- •Практическая работа № 2 Решение рациональных уравнений, неравенств, систем уравнений и неравенств второй степени
- •Средства обучения:
- •Практическая работа № 3 Вычисление приближенных значений.
- •Средства обучения:
- •Практическая работа № 4 Преобразование и вычисление числовых значений алгебраических выражений, содержащих степени с рациональными показателями
- •Средства обучения:
- •Практическая работа № 5 Преобразование и вычисление числовых значений алгебраических выражений, содержащих корни n-ой степени ( )
- •Средства обучения:
- •Практическая работа № 6 Преобразование и вычисление числовых значений алгебраических выражений, содержащих степени и корни
- •Средства обучения:
- •Практическая работа № 7 Решение иррациональных уравнений.
- •Практическая работа № 8 Вычисление логарифма числа с произвольным основанием
- •Средства обучения:
- •Практическая работа № 9 Вычисления логарифма числа с произвольным основанием
- •Средства обучения:
- •Практическая работа № 10 Преобразование и вычисление значений показательных и логарифмических выражений.
- •Средства обучения:
- •Практическая работа № 11 Решение показательных и логарифмических уравнений
- •Средства обучения:
Практическая работа № 6 Преобразование и вычисление числовых значений алгебраических выражений, содержащих степени и корни
Цель: научиться применять свойства степени и корня для преобразования алгебраических выражений.
Средства обучения:
методические рекомендации к практической работе № 6.
Виды самостоятельной работы:
сравнение выражений;
вычисление значения выражения с применением свойств степени и корня;
упрощение буквенных выражений с применением свойств степени и корня;
решение уравнений графическим способом;
решение уравнений путем введения новой переменной.
Краткая теоретическая справка
Если
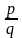 - обыкновенная дробь (
- обыкновенная дробь (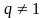 )
и
)
и
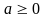 ,
то под
,
то под
 понимают
понимают
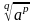 :
:
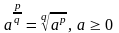 .
.
Если
- обыкновенная дробь (
)
и
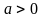 ,
то под
,
то под
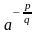 понимают
понимают
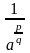 :
:
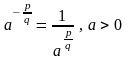 .
.
Для степени с рациональным показателем справедливы те же свойства, что и для степени с целым показателем.
Пусть a > 0, b > 0, r, s − любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.
ar · as = ar + s.
ar : as = ar – s.
(ar)s = ars.
(ab)r = ar · br .
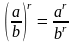 .
.
Практические задания
1. Расположить числа в порядке возрастания.
2. Найти значение выражения.
3. Упростить выражение.
Для аудиторной работы
1.
а)
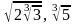 и
и
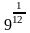 ; б)
; б)
 и
и
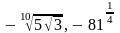 .
.
2.
а)
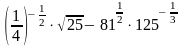 ; б)
; б)
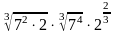 ; в)
; в)
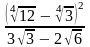 .
.
3.
а)
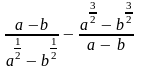 ; б)
; б)
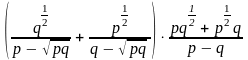 .
.
Для самостоятельной работы
Вариант 1
1.
а)
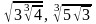 и
и
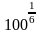 ; б)
; б)
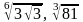 и
и
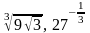 .
.
2.
а)
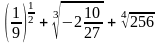 ; б)
; б)
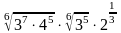 ; в)
; в)
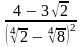 .
.
3.
а)
 ; б)
; б)
 .
.
Вариант 2
1.
а)
 и
и
 ; б)
; б)
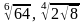 и
и
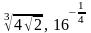 .
.
2.
а)
 ; б)
; б)
 ; в)
; в)
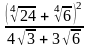 .
.
3.
а)
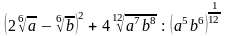 ; б)
; б)
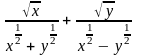 .
.
Вариант 3
1.
а)
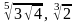 и
и
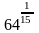 ; б)
; б)
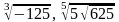 и
и
 .
.
2.
а)
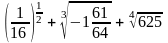 ; б)
; б)
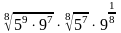 ; в)
; в)
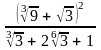 .
.
3.
а)
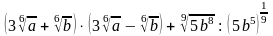 ;
б)
;
б)
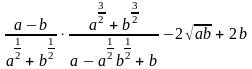 .
.
Вариант 4
1.
а)
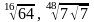 и
и
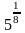 ; б)
; б)
 и
и
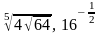 .
.
2.
а)
 ; б)
; б)
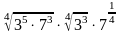 ; в)
; в)
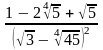 .
.
3.
а)
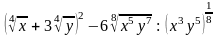 ; б)
; б)
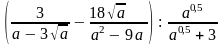 .
.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания 1-3.
2. Предоставить отчёт о выполненной работе, содержащей:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы;
- вывод о выполненном задании.
Контрольные вопросы
1. Что называют корнем n-й степени из действительного числа?
2. Свойства корня n-й степени.
3. Что понимают под , где n – натуральное число?
4. Что понимают под степенью с дробным показателем?
5. Что понимают под , где ?
6. Свойства степени с действительным показателем.
Сделайте вывод о том, какие математические навыки вы приобрели на этом занятии.
Практическая работа № 7 Решение иррациональных уравнений.
Цель: научиться применять на практике различные приемы и методы решения уравнений содержащих переменную под знаком радикала.
Средства обучения:
− методические рекомендации к практической работе № 7.
Виды самостоятельной работы.
− решение иррациональных уравнений;
− решение уравнений путем введения новой переменной.
− решение уравнений графическим способом.
Краткая теоретическая справка.
Уравнение, содержащее переменную под знаком корня, называются иррациональным.
Решение иррационального уравнения основано на преобразовании его к рациональному уравнению, что достигается возведением обеих его частей в одну и ту же степень (иногда несколько раз).
При возведении обеих частей иррационального уравнения в четвертую степень получается уравнение, являющееся следствием исходного. Уравнению – следствию удовлетворяют все корни исходного уравнения, но могут появиться и корни, которые не являются корнями исходного уравнения («посторонние» корни). Чтобы выявить «посторонние» корни, все найденные корни уравнения следствия проверяют подстановкой в исходное уравнение и «посторонние» корни отбрасывают.
Исходное иррациональное уравнение равносильно смешанной системе, состоящей из уравнения – следствия и ограничений, определяемых областью допустимых значений переменной. В этом случае «посторонние» корни не будут входить в область допустимых значений переменной, и проверять их подстановкой в исходное уравнение не требуется.
При возведении обеих частей иррационального уравнения в нечетную степень получается уравнение, равносильное исходному.
Практические задания для аудиторной работы.
1. Решите уравнение.
|
|
|
|
2. Решите уравнение.
|
|
|
|
3. Решите уравнение.
|
|
|
|
4. Решите уравнение.
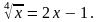
Для самостоятельной работы.
Вариант 1.
1. Решите уравнение.
|
|
|
|
2. Решите уравнение.
|
|
3. Решите уравнение.
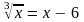
Вариант 2.
1. Решите уравнение.
|
|
|
|
2. Решите уравнение.
|
|
3. Решите уравнение.
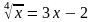
Вариант 3.
1. Решите уравнение.
|
|
|
|
2. Решите уравнение.
|
|
3. Решите уравнение.
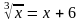
Вариант 4.
1. Решите уравнение.
|
|
|
|
2. Решите уравнение.
|
|
3. Решите уравнение.
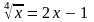
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания 1-3.
2. Предоставить отчёт о выполненной работе, содержащей:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы;
- вывод о выполненном задании.
Контрольные вопросы
1. Какие уравнения называются иррациональными?.
2. Как избавиться от иррациональности в уравнении?
3. Когда появляются «посторонние» корни?
Сделайте вывод о том, какие математические навыки вы приобрели на этом занятии.