
- •Содержание
- •Перечень практических работ
- •Практическая работа № 1 Выполнение действий с рациональными числами. Решение рациональных уравнений, неравенств, систем уравнений и неравенств первой степени.
- •Средства обучения:
- •Практическая работа № 2 Решение рациональных уравнений, неравенств, систем уравнений и неравенств второй степени
- •Средства обучения:
- •Практическая работа № 3 Вычисление приближенных значений.
- •Средства обучения:
- •Практическая работа № 4 Преобразование и вычисление числовых значений алгебраических выражений, содержащих степени с рациональными показателями
- •Средства обучения:
- •Практическая работа № 5 Преобразование и вычисление числовых значений алгебраических выражений, содержащих корни n-ой степени ( )
- •Средства обучения:
- •Практическая работа № 6 Преобразование и вычисление числовых значений алгебраических выражений, содержащих степени и корни
- •Средства обучения:
- •Практическая работа № 7 Решение иррациональных уравнений.
- •Практическая работа № 8 Вычисление логарифма числа с произвольным основанием
- •Средства обучения:
- •Практическая работа № 9 Вычисления логарифма числа с произвольным основанием
- •Средства обучения:
- •Практическая работа № 10 Преобразование и вычисление значений показательных и логарифмических выражений.
- •Средства обучения:
- •Практическая работа № 11 Решение показательных и логарифмических уравнений
- •Средства обучения:
Средства обучения:
методические рекомендации к практической работе № 3.
Виды самостоятельной работы:
нахождение погрешности приближения;
вычисление абсолютной и относительной погрешности приближения;
нахождение границ погрешностей приближений;
нахождение суммы, разности приближенных значений с учетом границ погрешностей;
нахождение произведения, частного приближенных значений с учетом границ погрешностей;
выполнение арифметический действий над приближенными значениями без учета границ погрешностей.
Краткая теоретическая справка
Если
результат измерения или вычисления
величины x
с некоторой точностью равен
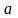 ,
то
называют приближенным
значением
(приближением) величины x.
,
то
называют приближенным
значением
(приближением) величины x.
Разность
между точным и приближенным значениями
величины называется погрешностью
приближения
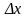 .
.
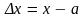
Модуль
разности между точным и приближенным
значениями величины называется абсолютной
погрешностью приближения
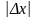 .
.
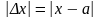
В случаях, когда неизвестно точное значение величины и из-за этого нельзя найти абсолютную погрешность приближения, указывают положительное число, больше которого абсолютная погрешность быть не может. Это число называют границей абсолютной погрешности.
Если
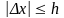 ,
то
,
то
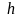 есть
граница абсолютной погрешности.
есть
граница абсолютной погрешности.
Тогда
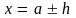 ,
т.е.
истинное значение величины x
заключается
в пределах
,
т.е.
истинное значение величины x
заключается
в пределах
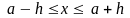 .
.
Для характеристики качества измерения используют понятие относительной погрешности. Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения.
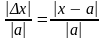
Любое положительное число, которое больше или равно относительной погрешности, называется границей относительной погрешности.
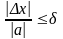 ,
где
,
где
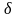 -
граница относительной погрешности.
-
граница относительной погрешности.
Если - граница абсолютной погрешности, то граница относительной погрешности равна
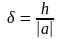 .
.
Если
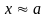 с точностью до
с точностью до
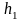 ,
,
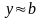 с точностью до
с точностью до
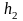 ,
то
,
то
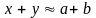 с
точностью до
с
точностью до
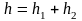 и
и
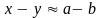 с точностью до
с точностью до
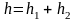 .
.
Если
с относительной точностью до
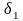 ,
с относительной точностью до
,
с относительной точностью до
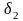 ,
то
,
то
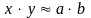 с
относительной точностью до
с
относительной точностью до
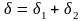 и
и
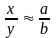 с относительной точностью до
.
с относительной точностью до
.
Если
с относительной точностью до
,
то относительная точность приближенного
равенства
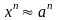 есть
есть
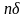 .
.
Граница относительной погрешности корня n-й степени в n раз меньше границы относительной погрешности подкоренного числа.
Практические задания для аудиторной работы
1.
Найти погрешность, абсолютную и
относительную погрешность приближенного
значения
величины
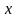 .
.
2. Определить точность приближенного равенства .
1.,2.
а)
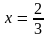 ;
;
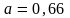 ;
б)
;
б)
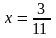 ;
;
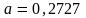 .
.
3. Определить относительную точность приближенного равенства .
а)
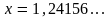 ;
;
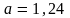 ;
б)
;
б)
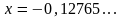 ;
;
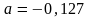 .
.
4.
Найти периметр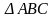 ,
если
,
если
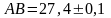 ,
,
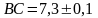 ,
,
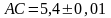 .
.
5.
Вычислить чему равна площадь прямоугольника
шириной
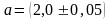 м
и длиной
м
и длиной
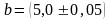 м.
м.
6.
Вычислить периметр четырехугольника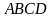 ,
если
,
если
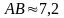 ,
,
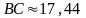 ,
,
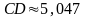 ,
,
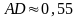 .
.
Практические задания для самостоятельной работы
Вариант 1
1.,2.
а)
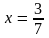 ;
;
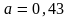 ;
б)
;
б)
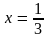 ;
;
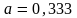 .
.
3.
а)
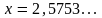 ;
;
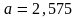 ;
б)
;
б)
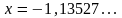 ;
;
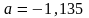 .
.
4.
Найти разность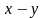 ,
если
,
если
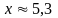 с точностью до 1%,
с точностью до 1%,
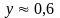 с
точностью до 2%.
с
точностью до 2%.
5.
Вычислить
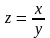 ,
если
,
если
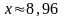 и
и
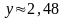 с точностью до 1%.
с точностью до 1%.
6.
Найти произведение чисел
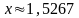 и
и
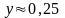 .
.
Вариант 2
1.,2.
а)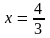 ;
;
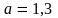 ;
б)
;
б)
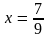 ;
;
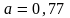 .
.
3.
а)
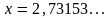 ;
;
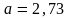 ;
б)
;
б)
 ;
;
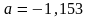 .
.
4.
Найти периметр прямоугольника
,
если
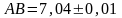 ,
,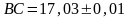 .
.
5.
Вычислить площадь ромба
,
если его диагонали равны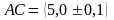 см,
см,
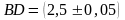 см.
см.
6.
Вычислить периметр
,
если
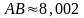 ,
,
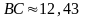 ,
,
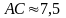 .
.
Вариант 3
1.,2.
а)
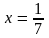 ;
;
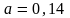 ;
б)
;
б)
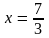 ;
;
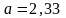 .
.
3.
а)
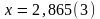 ;
;
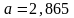 ;
б)
;
б)
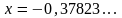 ;
;
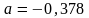 .
.
4.
Найти разность
,
если
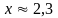 с точностью до 0,1%,
с точностью до 0,1%,
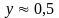 с
точностью до 1%.
с
точностью до 1%.
5.
Вычислить чему равна площадь прямоугольника
шириной
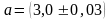 м
и длиной
м
и длиной
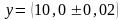 м.
м.
6.
Найти произведение чисел
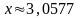 и
и
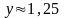 .
.
Вариант 4
1.,2.
а)
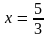 ;
;
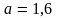 ;
б)
;
;
б)
;
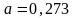 .
.
3.
а)
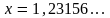 ;
;
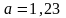 ;
б)
;
.
;
б)
;
.
4.
Найти периметр прямоугольника
,
если
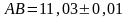 ,
,
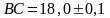 .
.
5.
Вычислить площадь ромба
,
если его диагонали равны
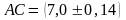 см,
см,
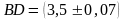 см.
см.
6.
Вычислить периметр
,
если
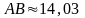 ,
,
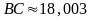 ,
,
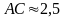 .
.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания.
2. Предоставить отчёт о выполненной работе, содержащей:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы;
- вывод о выполненном задании.
Контрольные вопросы
1. Что называют погрешностью приближения?
2. Что такое абсолютная погрешность приближения?
3. Какую погрешность называют относительной?
4. Что называют границами абсолютной и относительной погрешностей?
5. Какая существует связь между абсолютной и относительной погрешностями?
6. Чему равна погрешность суммы и разности приближенных значений?
7. Как вычислить погрешность произведения и частного приближенных значений?
8. Что такое верные и строго верные числа в записи приближенных значений?
9. Какие цифры в записи приближенного значения называют значащими?
10. Какими правилами пользуются при вычислениях без учета границ погрешностей?
Сделайте вывод о том, какие математические навыки вы приобрели на этом занятии.
