Контрольная работа состоит из десяти вариантов. Каждый вариант контрольной работы содержит 5 задач по темам «Множество» и «Комбинаторика».

Вариант контрольной работы определяется по списку группы 1-1, 2-1, 3-3, 4-4, 5-5, 6-6, 7-7, 8-8, 9-9, 10-10, 11-1, 12-2, 13-3, 14-4, 15-5 и т.д.

При выполнении контрольной работы необходимо соблюдать следующие требования:

1. в контрольную работу записывать контрольные вопросы и условия задач;

2. содержание ответов должно быть четким и кратким;

3. решение задач следует сопровождать пояснениями.

Выполненная работа должна содержать:

1. первый лист – титульный лист (ФИО, группа, вариант) ;

2. следующий лист – решенные задания.

Вариант 1

1.  Принадлежит ли число числовому множеству N, Z?

 0; 102; -1050.

2.  Приведите примеры: а) конечного множества; б) бесконечного множества.

3.  Даны множества: N= {1; 2; 3;…}, R={0; 0,5; 1; 1,5; 2}, 

A={-0,5; 0;0,5}, B={1; 2; 3; 4; 5}, D= {…-1; -0,5; 0; 0,5; 1,…}.

Выясните:

1) Какое из двух множеств является подмножеством другого: а) N или D; б) D или А; в) В или N.

2) а) N ∩ R=?; N ∩ А=?; N ∩ В=?; N ∩ D=?; A ∩ B=?; A ∩ D=?; B ∩ R=?;

 б) A ⋃ B; R ⋃ N; R ⋃ B.

4.  Сколько четырехзначных чисел можно составить из цифр 0, 1, 4,5, если цифры в записи числа не повторяются?

5.  Сколько существует трехзначных чисел, которые можно составить из цифр 6, 8, 1, используя каждую из них только один раз? Какие из полученных чисел делятся: а) на 2; б) на 4; в) на 3; г) на 6.

Вариант 2

1. Дано множество С={-4 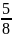; -3; 0; 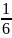; 8,3; 9; 12}. Выделите его подмножество, элементами которого являются: а) натуральные числа; б) целые числа; в) четные натуральные числа; г) целые неотрицательные числа; д) целые числа, кратные 3; е) положительные числа.

2.  Пусть М- множество чисел, кратных 2, а Р- множество чисел, кратных 3.

Найдите М ∩ Р, М ⋃ Р.

3. В классе 15 девочек. Из них 10 человек занимаются в музыкальной школе и 9- бальными танцами. Только одна из девочек не ходит ни в какую из данных секций. Сколько девочек занимаются в музыкальной школе и занимаются бальными танцами?

Подсказка. Начертите круги Эйлера.

4.  Танцевальная студия объявила дополнительных набор девочек от 10 до 12 лет. На просмотр пришли 4 девочки. Сколько есть вариантов отбора новеньких у руководителей студии?

5.  Сколькими способами можно разложить три разные по достоинству монеты в два кармана?

Подсказка. Достаточно учитывать только один карман.

Вариант 3

1. Известно, что D – множество деревьев в саду, F – множество фруктовых деревьев в этом саду, K – множество яблонь в этом саду. Установите, каковы отношения между парами этих множеств, если все они непусты. Изобразите множества D, F, K при помощи кругов Эйлера.

2. . Даны множества А={a,b,c,d} и В={a,d,r,l,m}.

Найдите множества A  B , A B, А\В, В\А.

3. Перечислите элементы декартова произведения множеств А={1,3,5} и В={2,4,6,8}.

4.  Сколько НЕчетных двузначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 7?

5. Сколько всего двузначных чисел можно составить из цифр 6,2 и 1 при условии, что они в записи числа не повторяются?

Вариант 4

1. А – множество натуральных чисел, кратных 7, В – множество натуральных чисел, кратных 3, С – множество четных натуральных чисел. Из каких чисел состоят множества: а) A B\ C ; б) AC \ B ;

в) A B\ C ; г) C  B \ A ;

2. Изобразите следующие множества геометрически: A B, A B, А\В, В\А, A B, A B, A B, A B, если А=(1;3], В=[-2;2).

3. Из 170 спортсменов 70 занимаются футболом, 95 – хоккеем и 80 – теннисом. 30 занимаются и футболом, и хоккеем, 35 – и футболом, и теннисом, 15 – и хоккеем, и теннисом. 5 занимаются всеми 3 видами спорта. Сколько занимаются ровно 1 видом спорта?

4. Сколько трехзначных чисел можно составить, используя цифры 3,2 и 1?

5. В финальном забеге по легкой атлетике участвуют спортсмены 9 стран. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами могут быть распределены медали между спринтерами?