Нормированное уравнение прямой.
Пусть прямая L не проходит через начало координат в ПДСК. Опустим из начала координат перпендикуляр на прямую L и пусть основанием этого перпендикуляра будет точка Р.
Обозначим
.
Вектор
всегда направлен от начала координат
к прямой. Он является единичным нормальным
вектором прямой.
– расстояние
от начала координат до прямой L.
-
угол наклона
к
оси
.
Пусть
M – текущая точка на прямой L;
- радиус-вектор точки M.
(26)
Угол
всегда острый
Тогда из (26) вытекает уравнение нормированное (нормальное) уравнение прямой.
(27)
Приведение общего уравнения прямой
к нормированному виду
(2)
Рассмотрим число (нормирующий множитель):
Умножим
уравнение (2) на
:
Обозначим:
(28)
Тогда
,
где
- расстояние от начала координат до
прямой
.
Знак
выбираем противоположно знаку
.
Отклонение точки от прямой.
Расстояние от точки до прямой
Отклонением
точки
от прямой L называется расстояние
от этой точки до прямой L, взятое со
знаком “+”, если точка
и начало координат O находятся по
разные стороны от прямой L, и со
знаком “–”, если
и O находятся по одну сторону от L.
Если O лежит на L, то знак не
определен.
Теорема 2 (об отклонении точки от прямой).
Пусть
уравнение прямой L имеет вид (27),
тогда отклонение
произвольной точки плоскости
от этой прямой равно
(29)
◄
,
,
Докажем,
что
,
- расстояние от
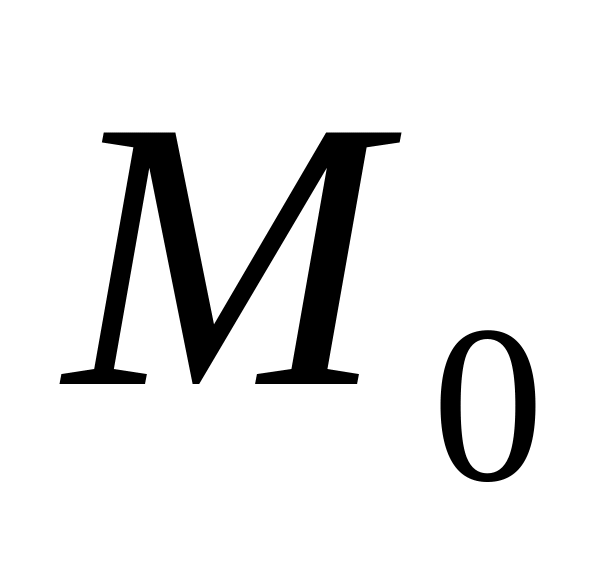до L.
Прямая
L разделяет плоскость на две
полуплоскости, а
направлен в ту полуплоскость, где
находится точка
.
Если
и O находятся по разные стороны от
L, то
сонаправлен с вектором
.
,
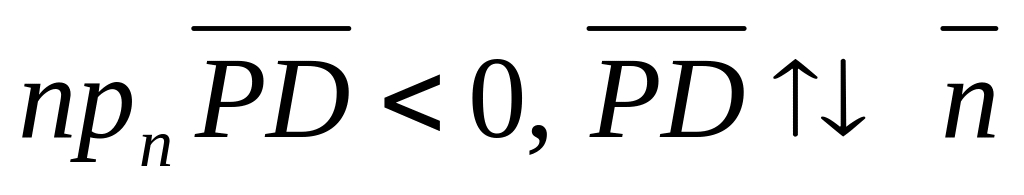тогда
направлен в ту полуплоскость, где
находится точка O, т.е.
и О находятся по одну сторону от
прямой L.
Следовательно,
по определению отклонения из п.п. 1 и 2
вытекает, что
.
Вычислим
:
►
Следствие:
Расстояние от точки
до прямой L, заданной нормированным
уравнением равно
(30)
(31)
Задача 4
Дан
треугольник с вершинами
.
Найти:
1) высоту, опущенную из вершины A;
2) уравнение биссектрисы внутреннего угла B.
Высота
- это
расстояние от точки
до прямой
.
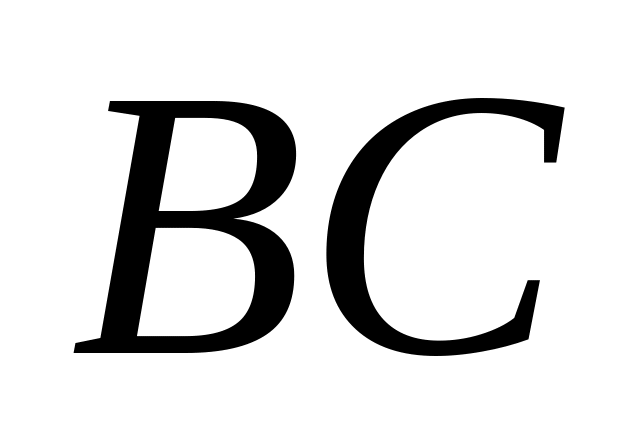Уравнение прямой
(проходящей через две точки):
.
Нормирующий
множитель:
Прямая
:
Запишем уравнение прямой
в нормированном виде:
Прямая
Если
биссектрисе,
то расстояния от т.
до прямых BA и BC равны между собой:
Два случая:
а)
б)
Подставляем в уравнение а):
Подставляем в уравнение б):
Для
уравнения б) точки находятся по разные
стороны от биссектрисы, уравнение б) –
искомая биссектриса.
Пучок прямых на плоскости
Определение
Пучком прямых на плоскости с центром в точке S называется множество всех прямых плоскости, проходящих через точку S.
Теорема 3 (о пучке прямых)
Пусть даны две прямые принадлежащие пучку прямых с центром в точке S
,
Тогда
прямая (при
)
(32)
есть уравнение некоторой прямой пучка с центром в точке S.
любая прямая пучка с центром в точке S имеет уравнение вида (32).
◄
Перегруппируем левую часть уравнения (32)
(32’)
Необходимо определить степень уравнения. Уравнение (32’) может быть:
а) первой степени;
б) нулевой степени.
Нулевая
степень будет тогда, и только тогда,
когда
и
равны одновременно нулю:
Пусть
Это
условие параллельности прямых
,
что противоречит условиям теоремы
данное уравнение имеет первую степень.
Пусть
- центр пучка.
имеется
система уравнений:
прямая
(32) принадлежит пучку с центром в точке
S.
Пусть
- произвольная точка плоскости, не
лежащая ни на одной из данных прямых.
Рассмотрим
прямую пучка L3, проходящую
через данную точку. Подставим координаты
в (32). Найдем
,
при которых данное уравнение верно для
.
Из (32):
Подставим
найденное
в
(32):
Подставим координаты точки и в уравнение, получим тождество. Данное уравнение является уравнением прямой , т.к. данному уравнению удовлетворяют координаты точек и . ►
Задача 5
Даны уравнения сторон треугольника:
Определить, не проходят ли они через одну точку (т.е., действительно ли это треугольник).
Задача 6
Найти уравнение прямой, на которой лежит высота, опущенная из вершины A.
Решение:
Составим
уравнение пучка прямых, которому
принадлежат прямые
и
Найдем угловой коэффициент:
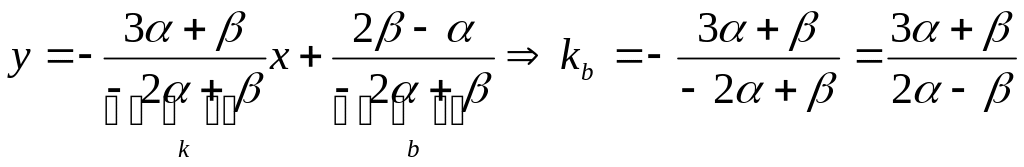
Из условия перпендикулярности прямых:
Подставляем
в уравнение пучка:
