
- •Линии на плоскости
- •Прямая линия на плоскости. Общее уравнение прямой
- •Неполные уравнения прямой.
- •Уравнение прямой в отрезках
- •Различные уравнения прямой на плоскости
- •Взаимное расположение двух прямых на плоскости
- •Условие перпендикулярности прямых
- •Нормированное уравнение прямой.
- •Пучок прямых на плоскости
Линии на плоскости
![]() (1)
(1)
Определение. Пусть на плоскости рассматривается линия L: уравнение (1) называется уравнением линии L, если любая точка на линии L имеет координаты в данной системе координат, которые удовлетворяют уравнению (1). И любая точка, не лежащая на линии L, имеет координаты, неудовлетворяющие уравнению (1).
Определение. Многочленом степени n от двух переменных (x и y) называется сумма, каждое слагаемое которой представляет произведение вида
![]() ,
,
при
этом имеется хотя бы одно слагаемое,
удовлетворяющее
![]() .
.
Определение. Уравнение (1), в котором функция представляет собой многочлен степени n от двух переменных, называется алгебраическим уравнением степени n.
Определение. Линии плоскости, описываемые алгебраическими уравнениям степени n, называются алгебраическими линиями n-го порядка.
Пример:
1.![]()
2.
![]()
Прямая линия на плоскости. Общее уравнение прямой
Лемма
Степень уравнения линии не зависит от выбора системы координат.
Общее уравнение прямой
(2)
Теорема 1
Любое уравнение первой степени от двух неизвестных (2) описывает прямую линию на плоскости. Любая прямая линия на плоскости описывается уравнением первой степени.
◄ Докажем,
что (2) уравнение прямой линии. Пусть
точки
![]() ,
,
![]() ,
,
![]() ,
где L – линия, описывающая (2).
,
где L – линия, описывающая (2).
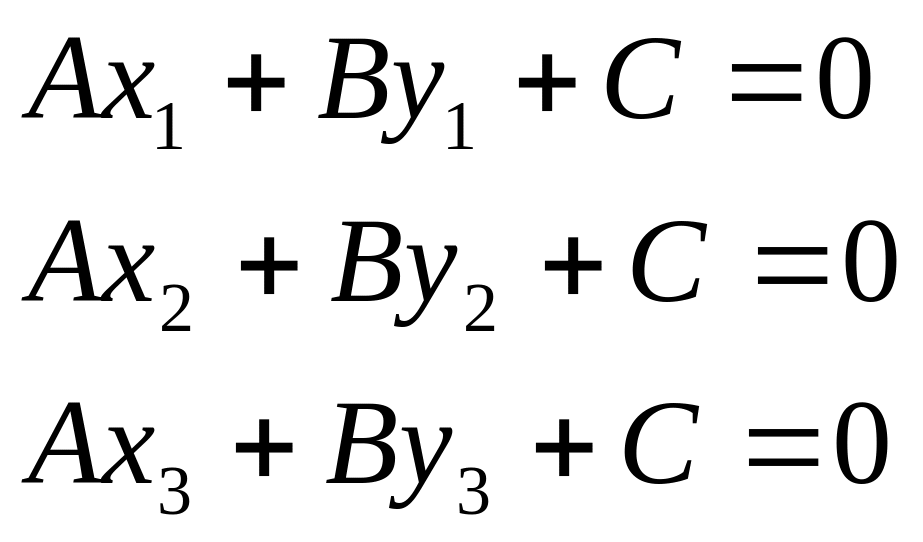
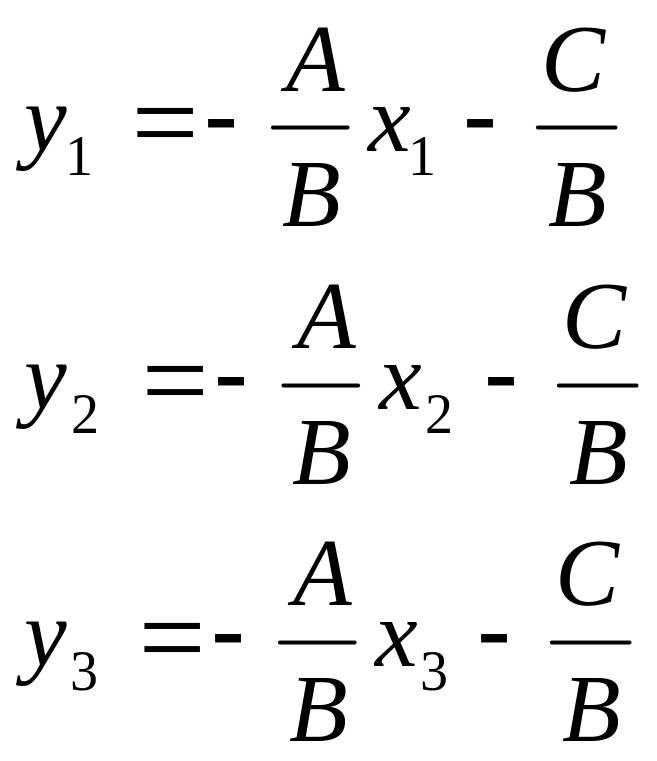

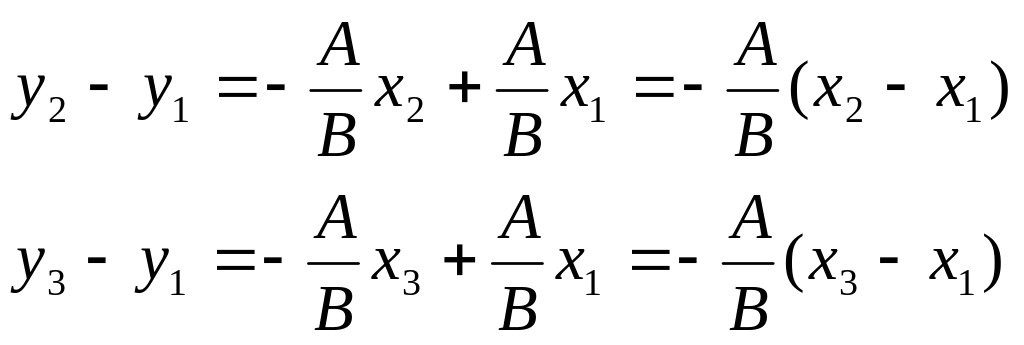

Следовательно,
три точки
![]() лежат на одной прямой. Ввиду произвольности
этих точек сделаем вывод, что (2) –
уравнение прямой.
лежат на одной прямой. Ввиду произвольности
этих точек сделаем вывод, что (2) –
уравнение прямой.
Пусть
L – прямая на плоскости. Пусть L
совпадает с осью
![]() в выбранной системе координат:
в выбранной системе координат:
![]() по определению. Это уравнение первой
степени. По лемме наша прямая описывается
уравнением первой степени в любой другой
системе координат.
по определению. Это уравнение первой
степени. По лемме наша прямая описывается
уравнением первой степени в любой другой
системе координат.
►
Уравнение прямой, проходящей через точку с данным нормальным вектором.
Пусть
![]() с уравнением (2), то есть
с уравнением (2), то есть
![]() (2’)
(2’)
Вычтем (2) – (2’):
![]() (3)
(3)
Введем обозначения
![]() ,
,
![]()
Если уравнение (2) рассматривается в прямоугольной декартовой системе координат (ПДСК) на плоскости, то условие (3) означает:
![]()
![]()
![]()
![]() .
.
- нормальный вектор прямой с уравнением (2).
Уравнение
(3) - уравнение прямой, проходящей
через точку
![]() с данным нормальным вектором.
с данным нормальным вектором.
Задача 1
Точка
![]() -
основание перпендикуляра, опущенного
из начала координат на прямую. Написать
уравнение прямой.
-
основание перпендикуляра, опущенного
из начала координат на прямую. Написать
уравнение прямой.
Нормальный
вектор
![]()


Неполные уравнения прямой.
Уравнение
(2) называется полным, если
![]() ,
т.е. ни один из коэффициентов не равен
нулю, иначе оно неполное.
,
т.е. ни один из коэффициентов не равен
нулю, иначе оно неполное.
Неполные уравнения прямой:
(прямая проходит через начало координат).
Уравнение прямой в отрезках
Полное уравнение прямой:
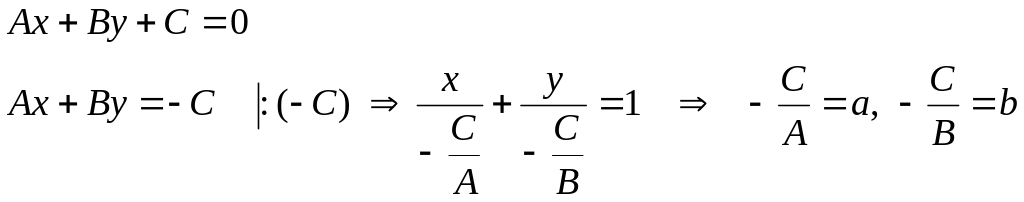
![]() (4)
(4)
Геометрический смысл коэффициентов a и b в уравнении (4)
Пересечем
![]() с
с
![]() ,
,
![]() ,
,![]() ,
,
(a; 0) – точка пересечения с .
Пересечем
с
![]() ,
,![]() ,
,![]() ,
,
(0; b) – точка пересечения с .
Уравнение
(4) называется уравнением
прямой в отрезках,
![]() и
и
![]() – координаты концов этих отрезков.
– координаты концов этих отрезков.
