Элементы комбинаторики и теории вероятностей. Элементы комбинаторики.
Группы, составленные из каких-либо элементов, называются соединениями.
Различают три основных вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различий соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся их решением, называется комбинаторикой.
Размещения. Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.
Число
размещений из n элементов
по m обозначается символом
и вычисляют по формуле:
(1.33)
Перестановки. Перестановками из n элементов называются такие соединения из всех n элементов, отличаются друг от друга порядком расположения элементов. Число перестановок из n элементов обозначается символом
.
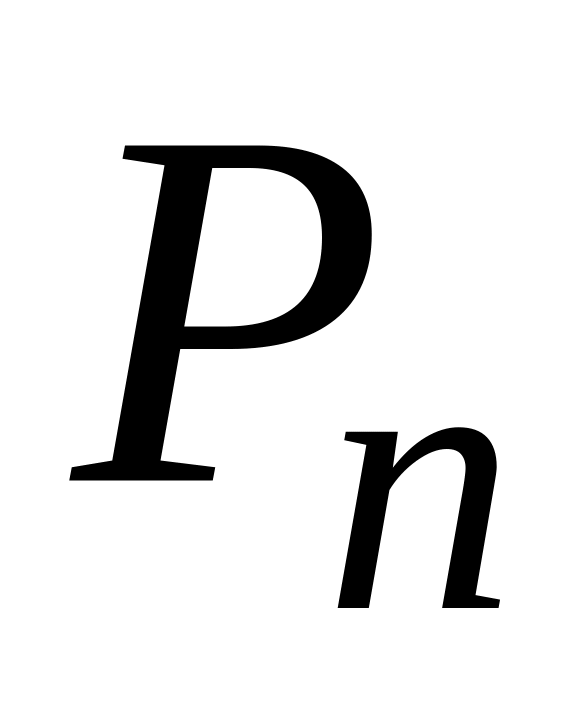(1.34)
Число всех
перестановок из n элементов
равно произведению последовательных
чисел от 1 до n включительно.
Произведение
обозначается символом n!
(читается «n – факториал»),
причем полагают 0!=1, 1!=1. Поэтому равенство
(1.34) можно переписать в виде:
(1.35)
Используя формулу (1.35), формуле (1.33) можно придать вид:
Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Число
сочетаний из n элементов
по m обозначается
.
Оно находится по формуле:
(1.36)
Которую можно записать также в виде:
(1.37)
Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:
(1.38)
(по
определению полагают
и
)
(1.39)
Найти число размещений: 1) из 10 элементов по 4; 2) из n+4 элементов по n-2.
Согласно формуле (1.33), получим:
1)
;
2)
Решить уравнение
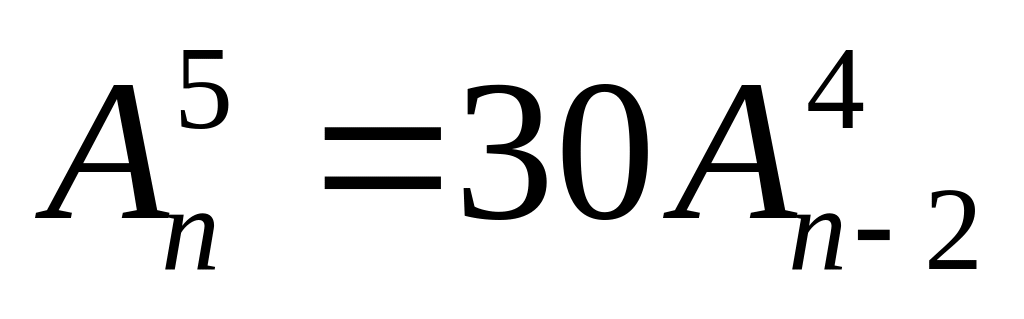
Используя
формулу (1.33), перепишем уравнение в виде
Учитывая,
что
,
разделим обе его части на
;
далее, имеем
Составить всевозможные перестановки из элементов 1) 1; 2) 5,6; 3) a,b,c.
(1);
;
2) (5,6); (6,5);
;
3) (a,b,c); (a,c,b); (b,c,a); (b,a,c); (c,b,a); (c,a,b);
Вычислить значения выражений: 1) 5!+6!; 2)
.
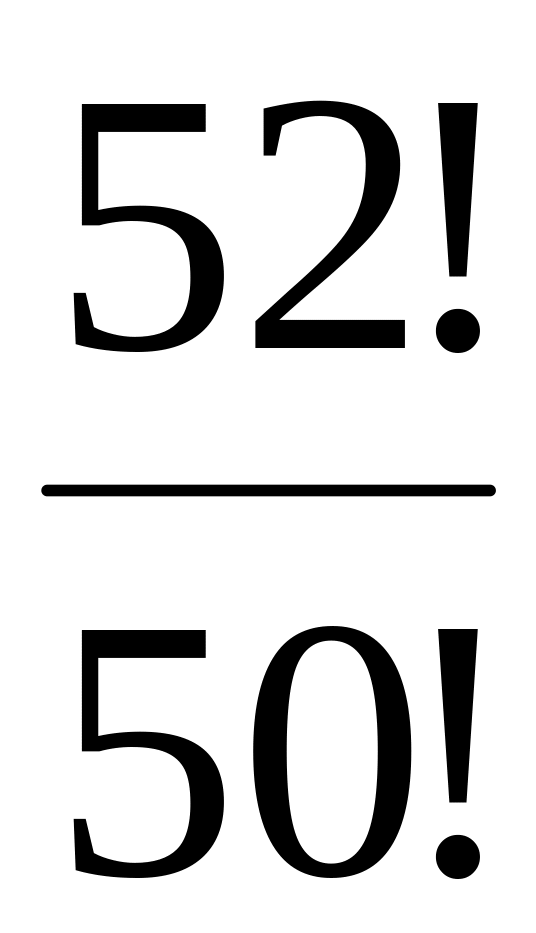1)
2)
Вычислить: 1)
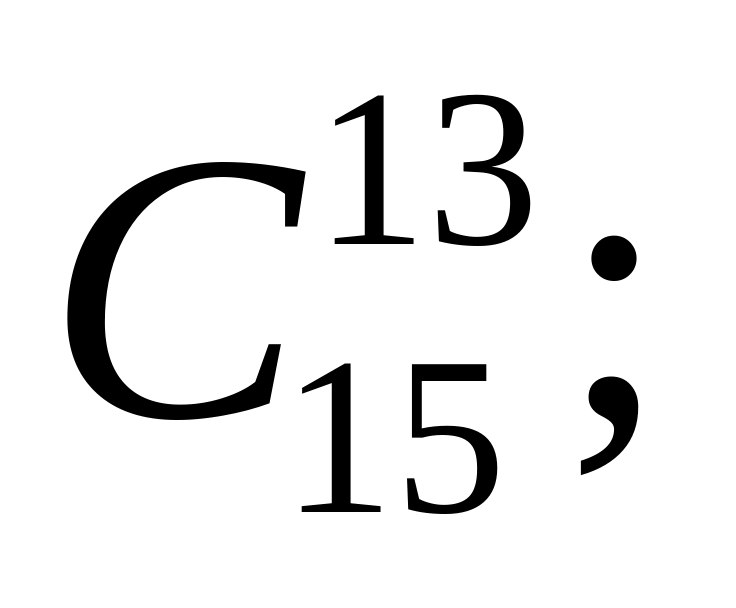2)
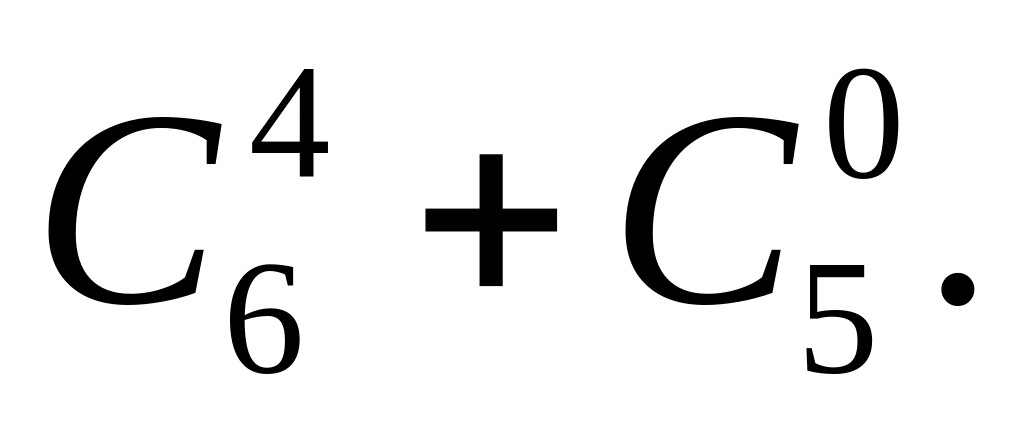
Согласно формуле (1.37), получим:
1)
2)
