
- •Аннотация
- •Введение.
- •I. Теория пределов. Вычислить предел функции:
- •II. Дифференциальное и интегральное исчисление Найти производные функции:
- •III. Вычислить интегралы
- •IV. Дифференциальные уравнения. Найти частные решения дифференциальных уравнений:
- •V. Основные понятия комбинаторики. Элементы теории вероятностей.
- •Вычисление предела функции
- •Производная. Производная сложной функции.
- •Основные правила дифференцирования. Производные степени и корня.
- •Неопределенный интеграл. Определенный интеграл. Основные формулы интегрирования. Непосредственное интегрирование.
- •1. Основные формулы интегрирования.
- •2. Непосредственное интегрирование.
- •Определенный интеграл. Определенный интеграл и его непосредственное вычисление.
- •Дифференциальные уравнения
- •Элементы комбинаторики и теории вероятностей. Элементы комбинаторики.
- •Случайные события. Вероятность события.
- •Теоремы умножения вероятностей
Определенный интеграл. Определенный интеграл и его непосредственное вычисление.
Пусть
функция
определена на отрезке
.
Разобьем этот отрезок на n
частей точками
![]() ,
выберем на каждом элементарном отрезке
,
выберем на каждом элементарном отрезке
![]() произвольную точку
произвольную точку
![]() и обозначим через
и обозначим через
![]() длину каждого такого отрезка. Интегральной
суммой для функции
на отрезке
называется сумма вида
длину каждого такого отрезка. Интегральной
суммой для функции
на отрезке
называется сумма вида
![]()
Определенным интегралом от функции , непрерывной на отрезке называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
![]()
Для
любой функции
,
непрерывной на отрезке
,
всегда существует определенный интеграл
![]() .
Для вычисления определенного интеграла
от функции
в том случае, когда можно найти
соответствующий определенный интеграл
,
служит формула Ньютона – Лейбница:
.
Для вычисления определенного интеграла
от функции
в том случае, когда можно найти
соответствующий определенный интеграл
,
служит формула Ньютона – Лейбница:
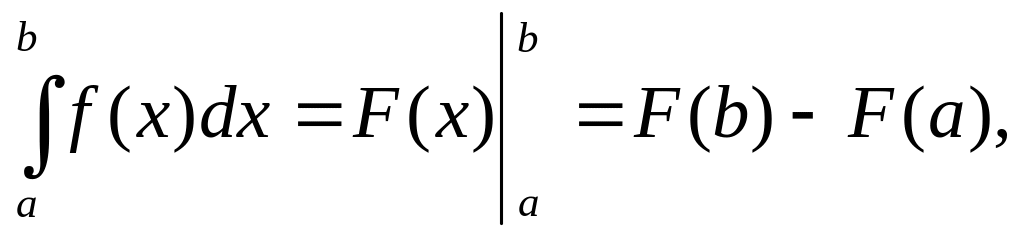
т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Вычислить следующие определенные интегралы:
1.
1)
![]() 2)
2)
![]() 3)
3)
![]()
По формуле Ньютона – Лейбница получаем:
1)
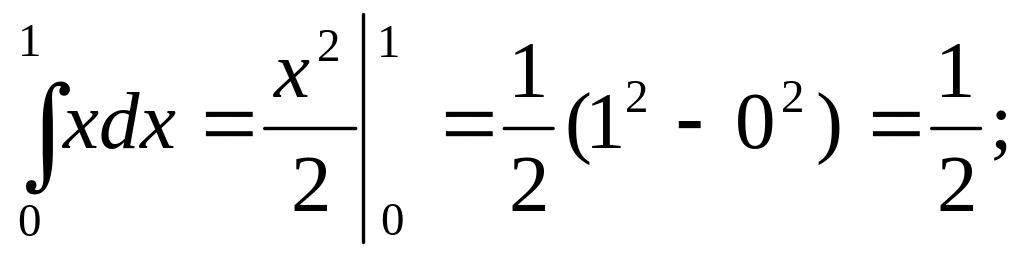
2)
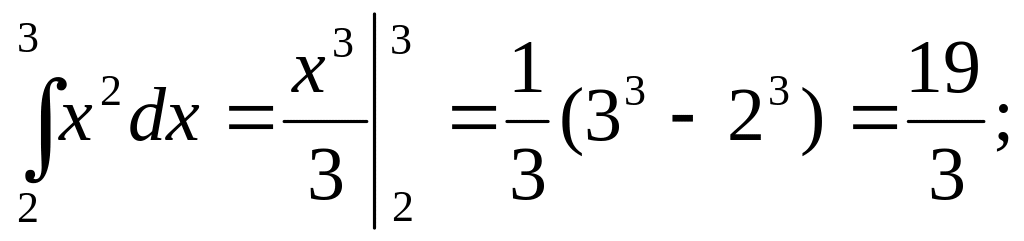
3)
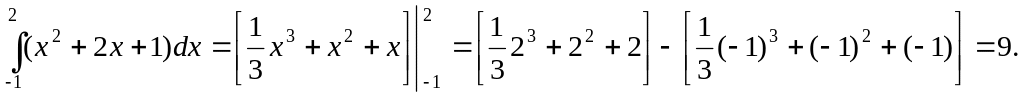
2.
1)
![]() 2)
2)
![]()
1)
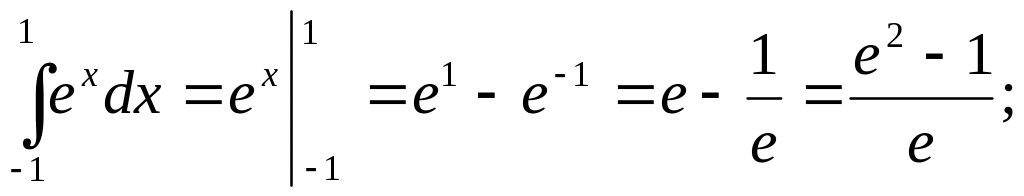
2)
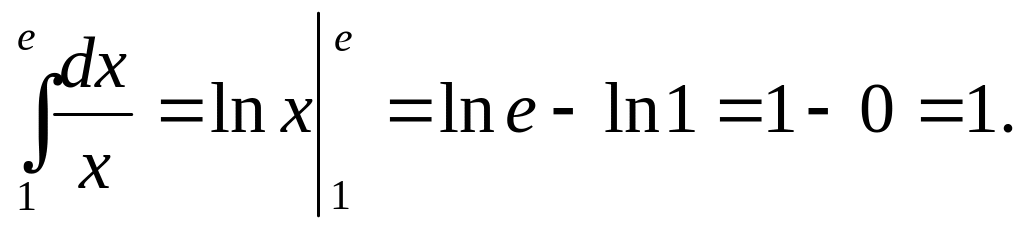
3.
1)
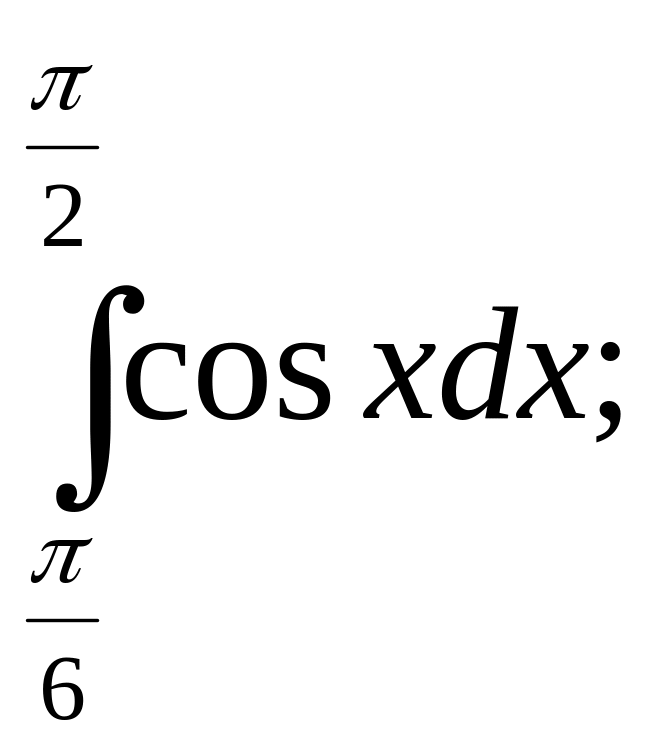 2)
2)

1)

2)

4.
1)
 2)
2)
![]()
1)
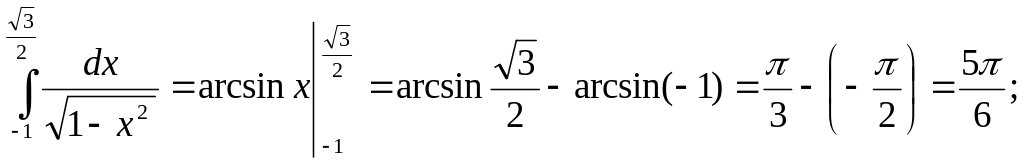
2)
Дифференциальные уравнения
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
![]()
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определённых начальных значениях аргумента и функции.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:
![]()
Для решения этого уравнения нужно сначала разделить переменные:
![]()
а затем проинтегрировать обе части полученного равенства:
![]()
1.Найти
общее решение уравнения
![]()
Разделив переменные, имеем:
![]()
Интегрируя обе части полученного уравнения:
![]()
Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо С мы написали (1/2)lnC. Потенцируя последнее равенство, получим:
![]()
Это и есть общее решение данного уравнения.
2.Найти
частное решение уравнения
![]() ,удовлетворяющее
начальным условиям
,удовлетворяющее
начальным условиям
![]() при
при
![]() .
.
Разделив переменные, имеем:
![]()
Проинтегрируем обе части полученного уравнения:
![]()
или
![]()
Это
общее решение данного уравнения .Для
нахождения значения произвольной
постоянной С подставим значения
![]() в выражение для общего решения:
в выражение для общего решения:
![]()
Следовательно,
искомое частное решение, удовлетворяющее
указанным начальным условиям, имеет
вид
![]()
