Неопределенный интеграл. Определенный интеграл. Основные формулы интегрирования. Непосредственное интегрирование.
1. Основные формулы интегрирования.
Функция
называется
первообразной для функции
в промежутке
,
если в любой точке этого промежутка ее
производная равно
:
Отыскание
первообразной функции по заданной ее
производной
или по дифференциалу
есть действие, обратное дифференцированию,
- интегрирование. Совокупность
первообразных для функции
или для дифференциала
называется неопределенным интегралом
и обозначается символом
.
Таким образом,
если
Здесь – подынтегральная функция; – подынтегральное выражение; С – произвольная постоянная.
Приведем основные свойства неопределенного интеграла.
1) Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:
2) Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
3) Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:
4) Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:
5)
Если
и
– любая известная функция, имеющая
непрерывную производную, то
Основные формулы интегрирования
(табличные интегралы).
(1.20.)
(1.21.)
(1.22.)
(1.23.)
(1.24.)
(1.25.)
(1.26.)
(1.27.)
(1.28.)
(1.29.)
(1.30.)
(1.31.)
(1.32.)
При применении формул (1.22.), (1.29.) и (1.30.) знак абсолютной величины пишется только в тех случаях, когда выражение, стоящее под знаком логарифма, может иметь отрицательное значение. Каждую из формул легко проверить. В результате дифференцирования правой части получается подынтегральное выражение.
2. Непосредственное интегрирование.
Непосредственное интегрирование основано на прямом использовании таблицы интегралов. Здесь могут представиться следующие случаи:
1) данный интеграл находится непосредственно по соответствующему табличному интегралу;
2) данный интеграл после применения свойств 3 и 4 приводится к одному или нескольким табличным интегралам;
3) данный интеграл после элементарных тождественных преобразований над подынтегральной функцией и применения свойств 3 и 4 приводится к одному или нескольким табличным интегралам.
Найти следующие интегралы:
1.
1)
2)
3)
4)
5)
1) На основании
свойства 4 постоянный множитель 5 выносим
за знак интеграла и, используя формулу
1.20., получим
2) Используя
свойство 4 и формулу 1.21., получим
Проверка:
Получили подынтегральное выражение;
следовательно, интеграл найден правильно.
3) Используя
свойства 3 и 4 и формулы 1.21. и 1.20., имеем
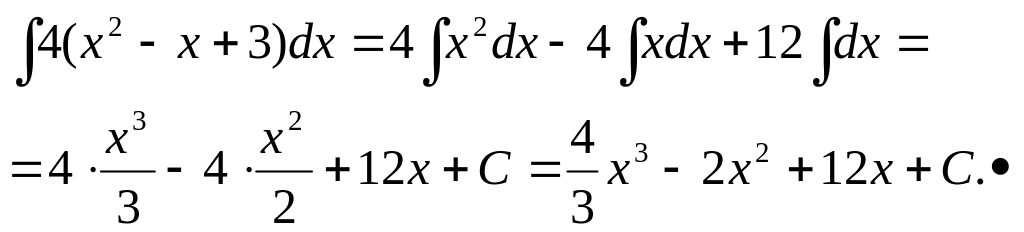
Постоянная
интегрирования С равна алгебраической
сумме трех постоянных интегрирования,
так как каждый интеграл имеет свою
произвольную постоянную
4)
5)
2.
1)
2)
.
1)
2)
3.
1)
2)
3)
1) По формуле 1.22.
находим
2) Так как
,
то
3) Так как
,
то
Знак абсолютной
величины не пишем, так как при любом
значении х выражение
4.
1)
2)
3)
1) По формуле 1.23.
при
получим
2) Так как
,
то
3) Так как
,
то
5.
1)
2)
3)
1) так как
то
Следовательно,
2) Так как
то
3) Так как
,
то
6.
1)
2)
3)
4)
1) По формуле 1.27.
находим
2) Так как
то
.
Следовательно,
3) По формуле 1.18.
находим
4) Так как
,
то
7.
1)
2)
1) По формуле 1.29.
получаем
2) По формуле 1.30.
находим
8.
1)
2)
3)
4)
1) По формуле 1.31.
находим
2)
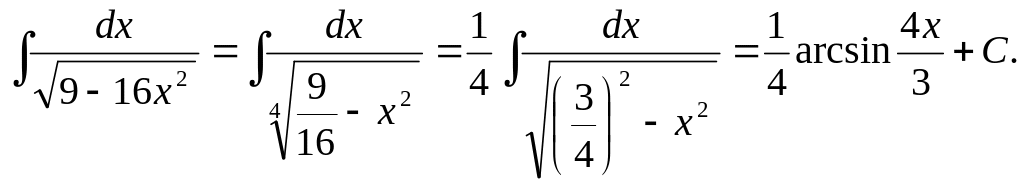
3) По формуле 1.32.
находим
4)
