Производная. Производная сложной функции.

Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента, когда последнее стремится к нулю:

Функция , имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке. Для производной функции употребляются следующие обозначения: или . Нахождение производной называется дифференцированием.

Основные правила дифференцирования. Производные степени и корня.

Основные правила дифференцирования.

Обозначения: С – постоянная; х – аргумент; u, v, w – функции от х, имеющие производные.

Производная алгебраической суммы функций

(1.1.)

Производная произведения двух функций

. (1.2.)

Производная произведения трех функций

(1.3.)

Производная произведения постоянной на функцию

(1.4.)

Производная частного (дроби)

(1.5.)

Частные случаи формулы (1.5.)

(1.6.)

(1.7.)

Если у есть функция от u: , где u, в свою очередь есть функция от аргумента х: , т.е. если у зависит от х через промежуточный аргумент u, то у называется сложной функцией от х (функцией от функции): Производная сложной функции равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:

, или

Исходя из этого соотношения, можно получить формулы дифференцирования сложных функций. При вычислении производных необходимо помнить, что (по определению)

и знать следующие правила действий со степенями и корнями:

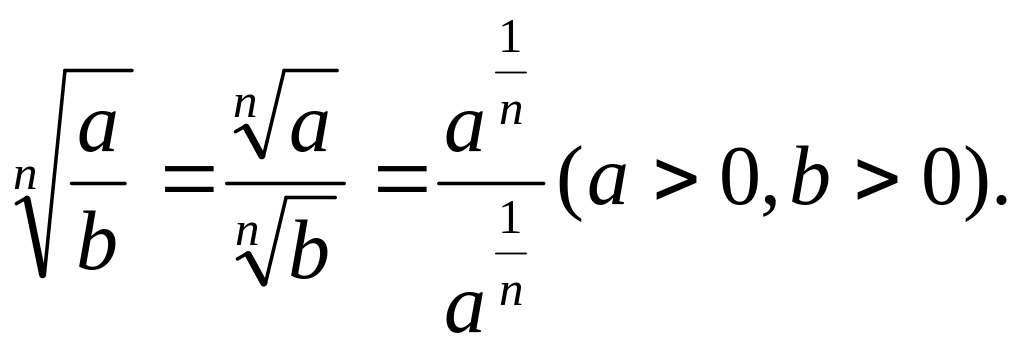
Здесь m и n – любые рациональные числа.

Формулы дифференцирования

При условии	Номер формулы	При условии	Номер формулы
			1.8.
			1.9.
где n-любое действительное число	1.10.	где n-любое действительное число	1.10.а
	1.11.		1.11.а
	1.12.		1.12.а

Найти производные следующих функций:

1. 1) ; 2) ; 3) ; 4) ; 5) .

1) Используя формулу (1.4.), вынесем постоянный множитель за знак производной, а затем применим формулу (1.10.а);



Аналогично, используя формулы (1.4.) и (1.10.а), получим:

2) 

3) 

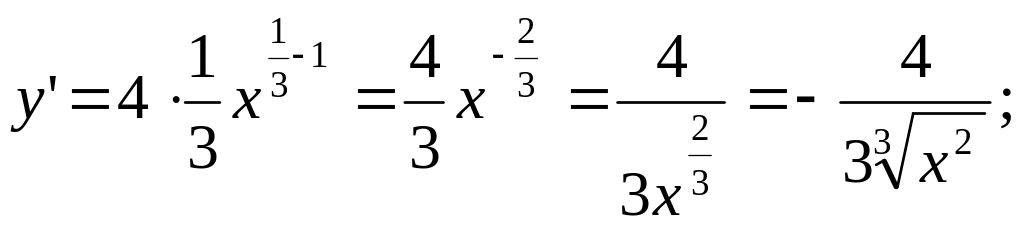
4) ;

5) 

Производная сложной функции

Найти производные следующих функций:

2.

Полагая , получим . По формуле (1.10.) находим 

Такая подробная запись производится только в процессе освоения техники дифференцирования. При навыке промежуточные вычисления производятся в уме.

3.

I способ. Применим последовательно формулы (1.11.) и (1.10.):

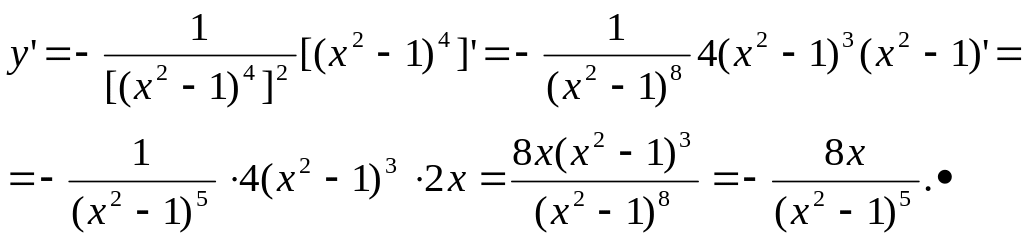
II способ. Введем отрицательный показатель и применим формулу (1.10.): 

4.

Полагая , получим . По формуле (1.12.) находим 

5.

Заменим кубический корень дробным показателем и по формуле (1.10.) найдем производную степени:



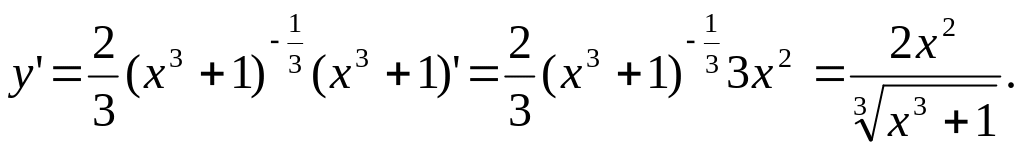
Производные логарифмических функций.

Формулы дифференцирования.

При условии	Номер формулы	При условии	Номер формулы
	1.13.		1.13.a
	1.14.		1.14.a

6.

По формуле (1.13.) получим:



Производные показательных функций.

Формулы дифференцирования.

При условии	Номер формулы	При условии	Номер формулы
	1.15.		1.15.a
	1.16.		1.16.a

7.

По формулам (1.1.), (1.15.а), (1.16.а) и (1.4.) получим:



8.

По формуле (1.15.) получим:



9. ;

По формуле (1.16.) находим:



Производные тригонометрических функций.

Формулы дифференцирования.

При условии	Номер формулы	При условии	Номер формулы
	1.17.		1.17.а
	1.18.		1.18.а
	1.19.		1.19.а
	1.20.		1.20.а

Найдите производные следующих функций:

10.

Полагая получим По формуле (1.17.) находим 

11.

Полагая , получим Применяя последовательно формулы (1.10.) и (1.17.), получим