Вычисление предела функции
1.
Число А называется пределом функции
при
,
если для любого числа
можно указать такое
,
что для любого
,
удовлетворяющего неравенству
,
выполняется неравенство
.
В этом случае пишут
.
Если число А1 (число А2)
есть предел функции
при х, стремящемся к
так, что х принимает только значения,
меньшие (большие)
,
то А1 (А2)
называется левым (правым) пределом
функции
в точке
.
При этом соответственно пишут
2.
Функция
называется бесконечно малой при
,
если
.
3.
Функция
называется
бесконечно большой при
,
если
,
или
,
или
.
Отметим свойства бесконечно малых и бесконечно больших функций.
Если функция и
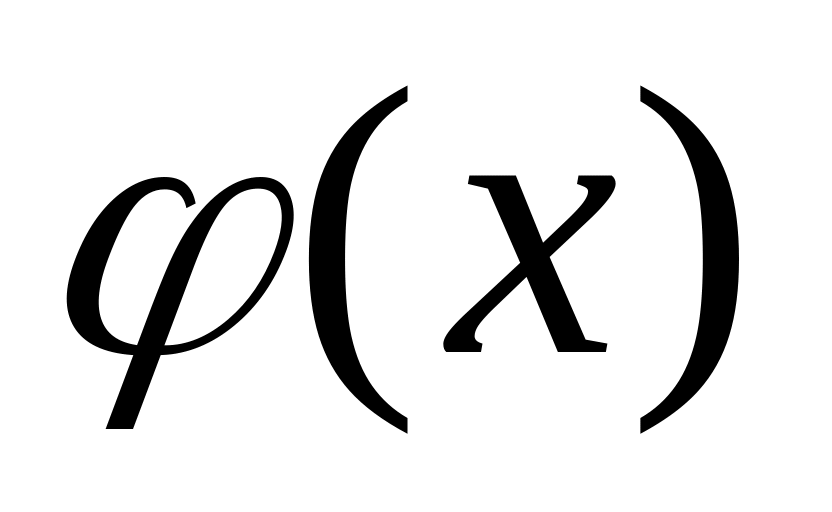– бесконечно малые при
,
то их сумма
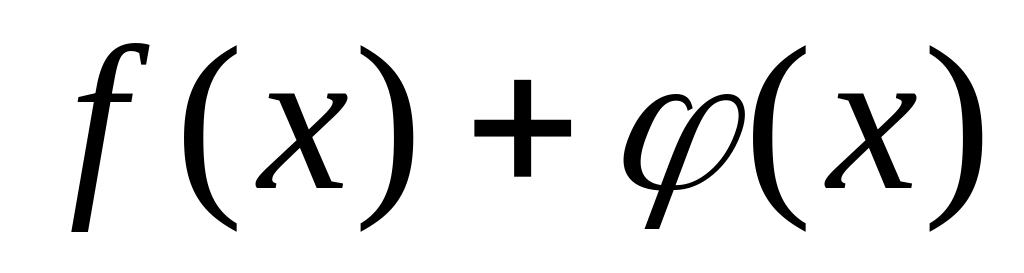при
также является бесконечно малой.Если функция – бесконечно малая при , а
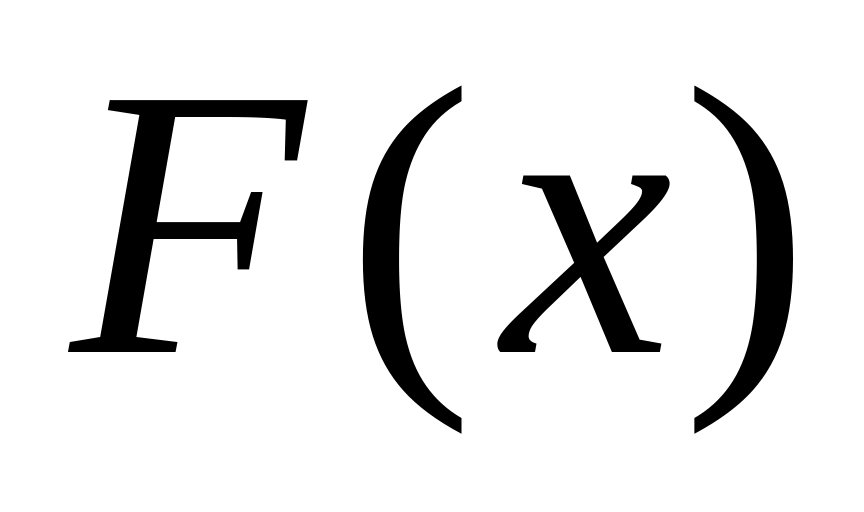– ограниченная функция, то их произведение
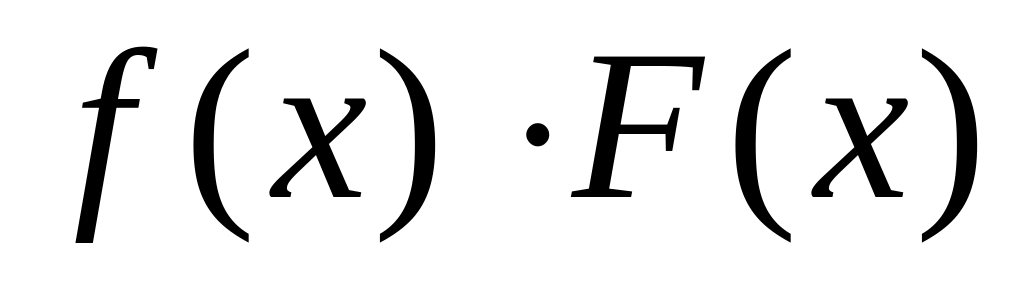есть функция бесконечно малая.
Следствие. Произведение конечного числа бесконечно малых функций есть величина бесконечно малая.
Если при функция имеет конечный предел , а функция – бесконечно большая, то
Если функция – бесконечно малая при , то функция
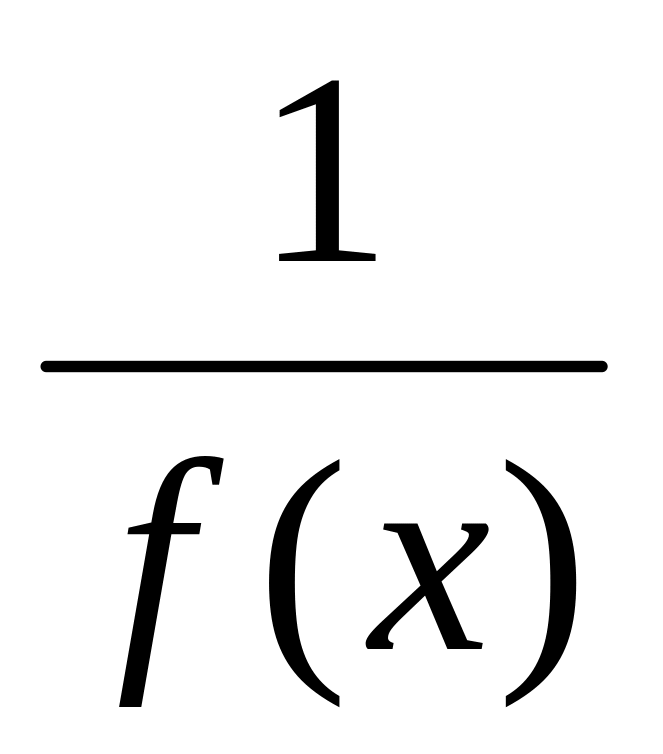– бесконечно большая, причем
предполагается, что в окрестности точки
а функция
не
обращается в нуль. Наоборот, если при
функция
– бесконечно большая, то функция
– бесконечно малая. Между бесконечно
малой функцией и функцией, имеющей
конечный предел, существует следующая
зависимость. Если функция
имеет конечный предел при
,
то ее можно представить в виде суммы
постоянной и бесконечно малой функции
при
.
Наоборот, если функция
может быть представлена в виде суммы
постоянной и бесконечно малой функции
при
,
то эта функция имеет конечный предел
при
,
который равен значению постоянной.
4. Теорема 1. Если существуют пределы функций и , то существует также и предел их суммы, равный сумме пределов функций и :
Теорема 2. Если существуют пределы функций и при , то существует также и предел их произведения, равный произведению пределов функций и :
Теорема
3. Если существуют пределы функций
и
при
и предел функции
отличен от нуля, то существует также
предел отношения
,
равный отношению пределов функций
и
:
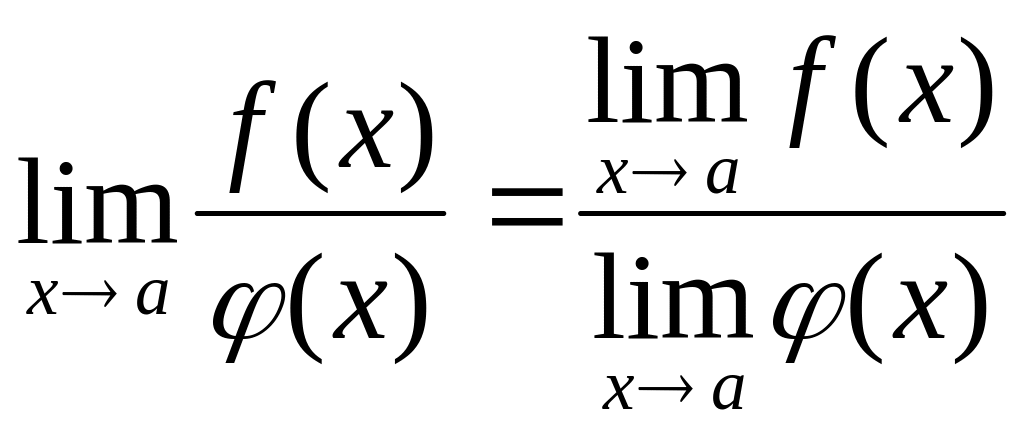
Следствия.
1.
Постоянный множитель можно вынести за
знак предела:
2.
Если n – натуральное
число, то
3.
Предел многочлена (целой рациональной
функции)
4.
Предел дробно-рациональной функции
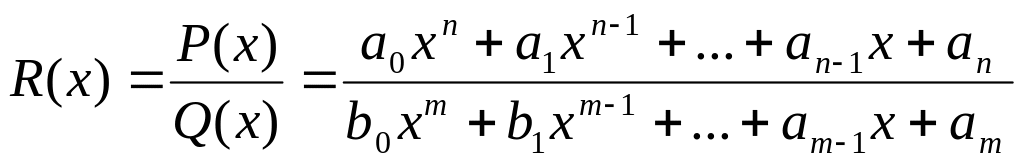при
равен значению этой функции при
,
если
принадлежит области определения функции,
т.е.
.
Вычислите пределы:
1.
1)
;
2)
.
1) По правилу нахождения предела многочлена находим
.
2) Так как при
знаменатель дроби отличен от нуля, то
по правилу нахождения предела
дробно-рациональной функции получим
2.
1)
;
2)
;
3)
.
1) Здесь предел
делителя равен нулю:
.
Следовательно, теорему о пределе частного
применить нельзя. Так как
,
то
при
есть величина бесконечно малая, а
обратная ей величина
– бесконечно большая. Поэтому при
произведение
есть величина бесконечно большая, т.е.
2) Здесь пределы
числителя и знаменателя при
равны нулю. Непосредственной подстановкой
вместо аргумента его предельного
значения вычислить предел нельзя, так
как при
получается отношение двух бесконечно
малых величин. Разложим числитель и
знаменатель на множители, чтобы сократить
дробь на общий множитель стремящийся
к нулю, и, следовательно, сделать возможным
применение теоремы 3. Нужно иметь в виду,
что здесь не производится сокращение
на нуль, что недопустимо. По определению
предела функции аргумент х стремится
к своему предельному значению, никогда
не принимая этого значения; поэтому до
перехода к пределу можно произвести
сокращение на множитель, стремящийся
к нулю. Имеем
3) Пределы числителя
и знаменателя при
равны нулю:
,
.
Разложим квадратный трехчлен в числителе
на линейные множители по формуле
,
где
и
– корни трехчлена. Разложив на множители
и знаменатель, сократим дробь на
.
Используя следствие 4, получим
3.
1)
;
2)
;
3)
.
1) При
знаменатель
неограниченно растет, т.е. является
величиной бесконечно большой, а обратная
величина
– бесконечно малой. Произведение
бесконечно малой на ограниченную
величину (постоянная – частный случай
ограниченной величины) есть величина
бесконечно малая, и предел ее при
равен нулю. Следовательно,
2) При
числитель и знаменатель – величины
бесконечно большие. Поэтому при
непосредственном применении теоремы
3 получаем выражение
,
которое представляет собой неопределенность.
Для вычисления предела этой функции
можно числитель и знаменатель разделить
на х:
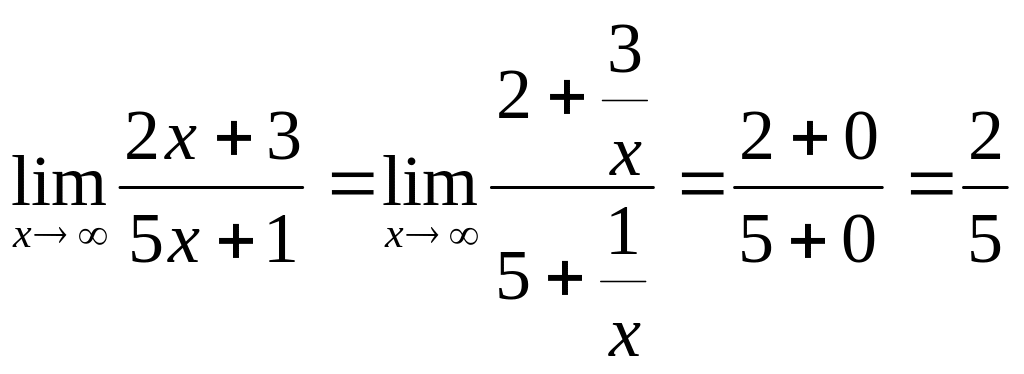
(при
слагаемые
и
– величины бесконечно малые и,
следовательно, их пределы равны нулю).
3)
Разделим числитель и знаменатель на
наивысшую степень аргумента в знаменателе,
т.е. на
:
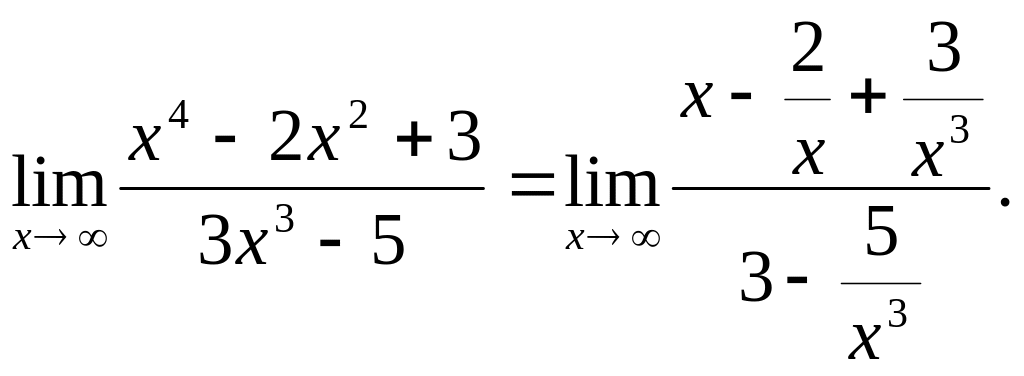
При имеем
и
Так как знаменатель есть величина ограниченная, то
