Контрольная работа №2.

Введение в математический анализ.

Дифференциальное исчичление.

41-50. Найти пределы функций.

41.

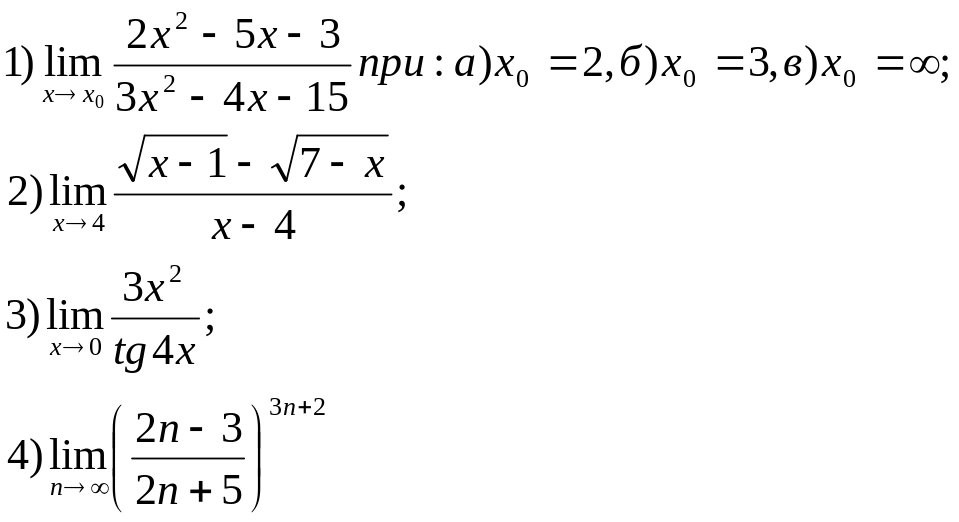
42.

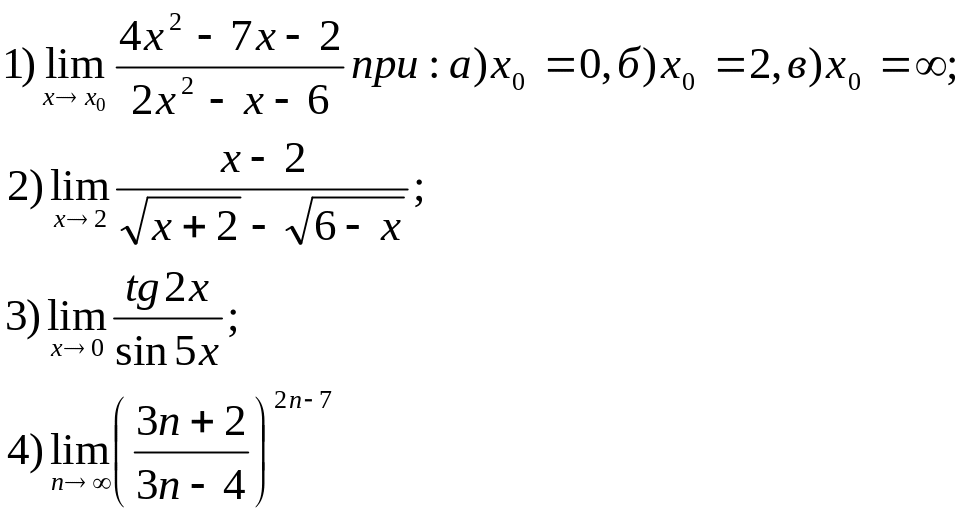
43.

44.

45.

46.

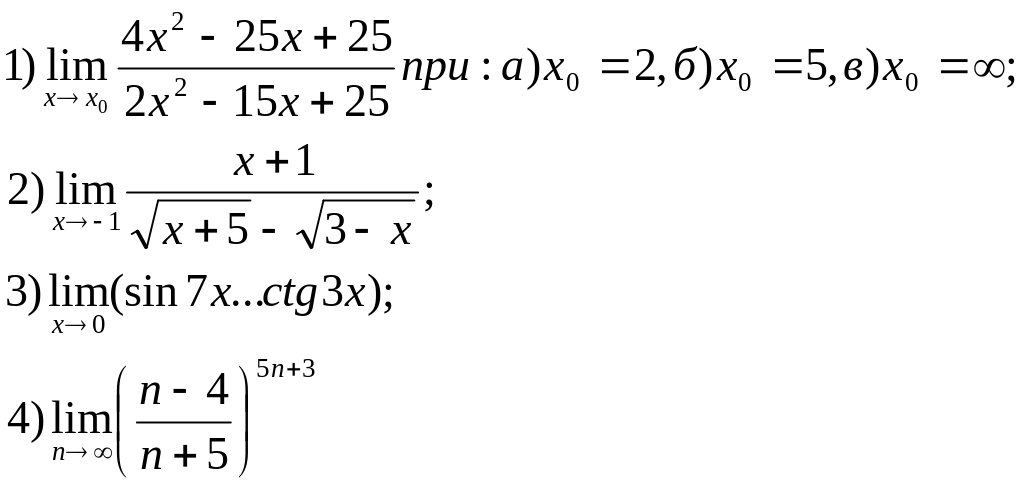
47.

48.

49.

50.

51-60. Найти производные заданных функций.

51.

52.

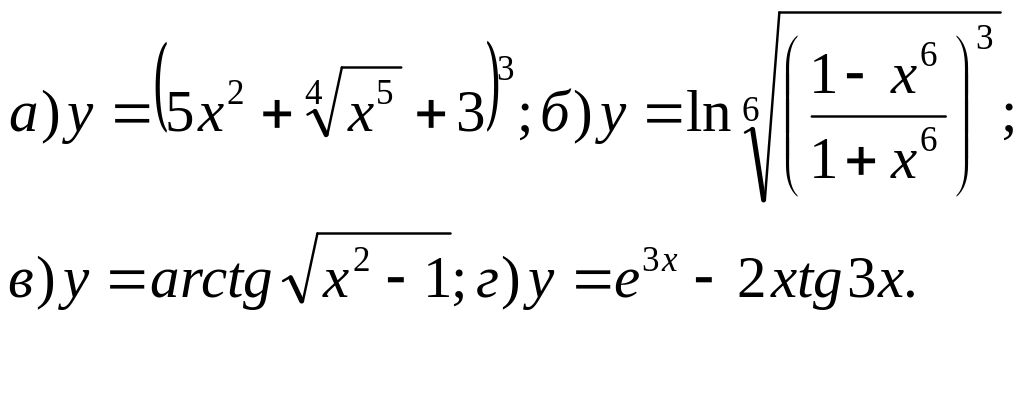
53.

54.

55.

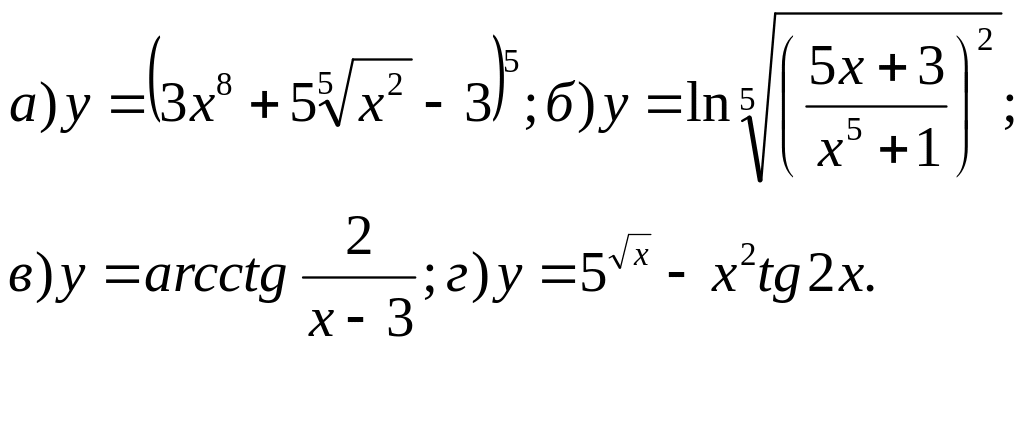
56.

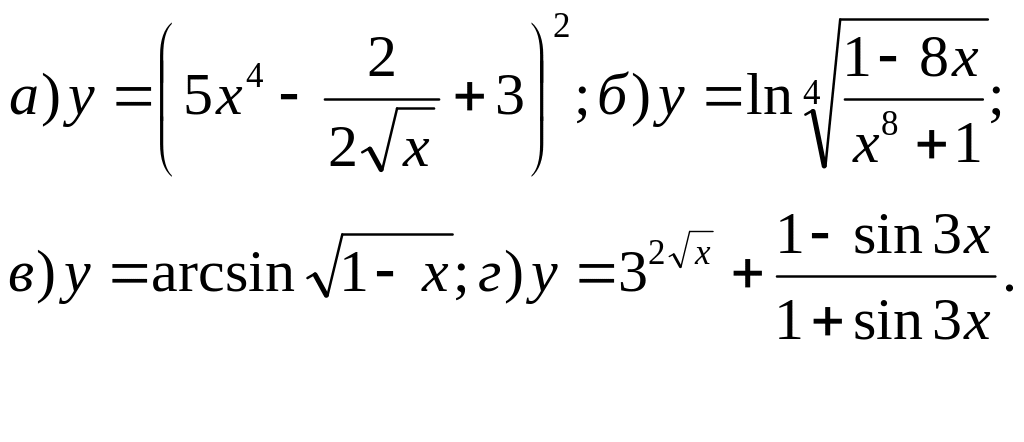
57.

58.

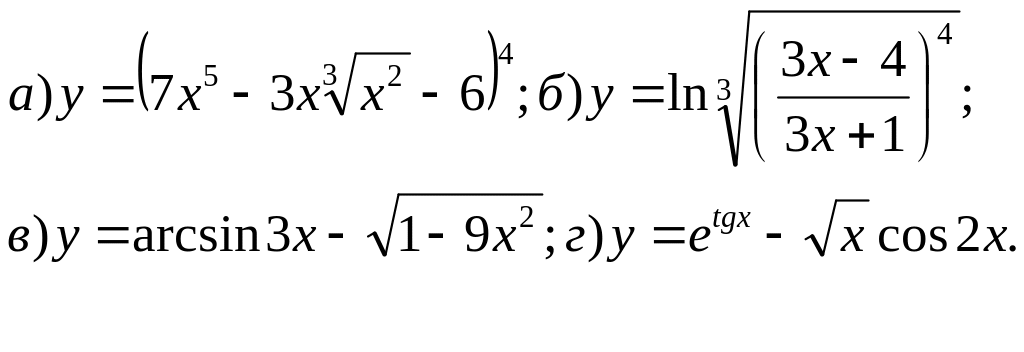
59.

60.

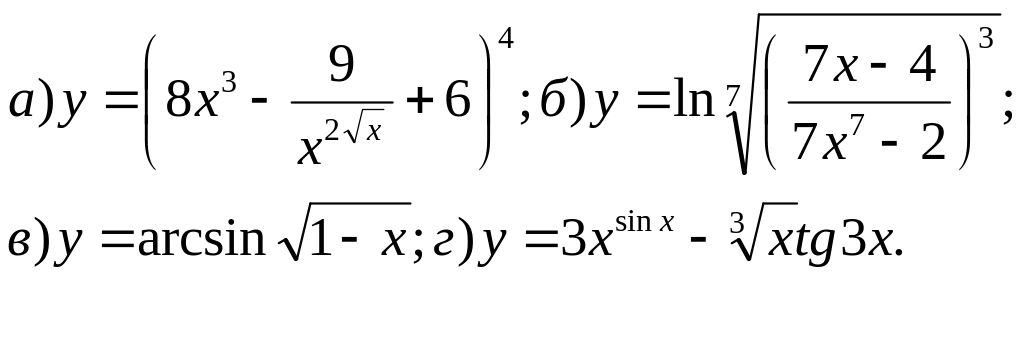
71-80. Исследовать средствами дифференциального исчисления функцию

у =f(x) и построить её график.

71.

72.

73.

74.

75.

76.

77.

78.

79.

80.

81-90. Найти полный дифференциал функции z = f(x;y).

81.

82.

83.

84.

85.

86.

87.

88.

89.

90.

Контрольная работа №3.

Интегральное исчисление.

91-100. Найти неопределённые интегралы. Результат проверить

дифференцированием.

91.

92.

93.

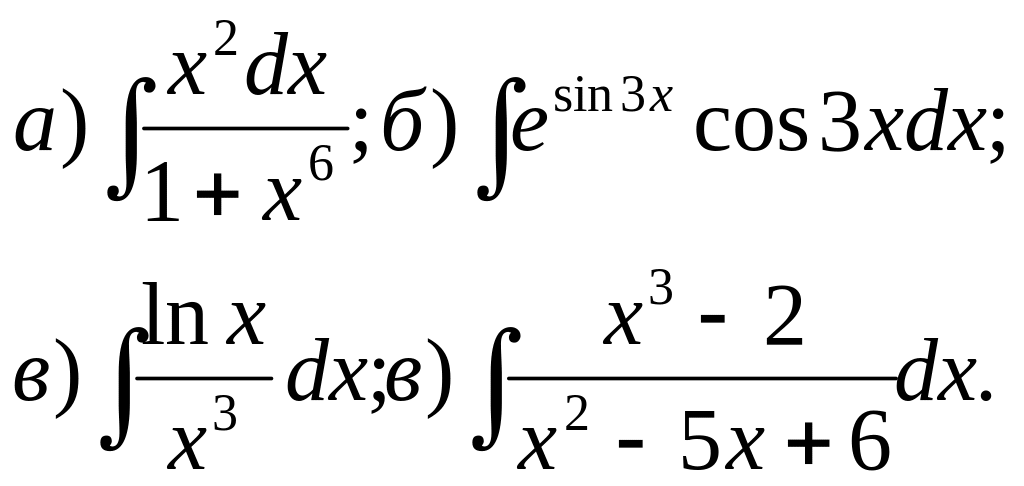
94.

95.

96.

97.

98.

99.

100.

101- 110. Вычислить по формуле Ньютона- Лейбница определенный

интеграл .

101. . 102. . 103.

104. . 105. . 106. .

107. . 108. . 109. .

110. .

111-120. Вычислить площадь фигуры, ограниченной параболой

и прямой у = кх+1. Сделать чертёж.

111. у = - х -1.

112. у = х + 1.

113. у = х - 5.

114. у = - х + 1.

115. у = - х + 1.

116. у = х + 1.

117. у = х + 1.

118. у = - х + 1.

119. у = - х -1.

120. у = х + 1.

Контрольная работа №4.

Дифференциальные уравнения. Ряды.

Теория вероятностей.

121-130. Найти общее решение дифференциального уравнения а(х)у + в(х)у= f(x)

и частное решение, удовлетворяющее начальному условию

у = у0 при х = х0.

121.

122.

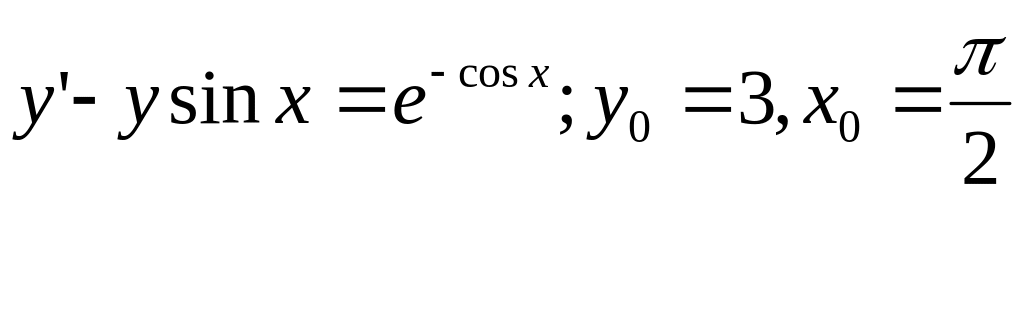
123.

124.

125.

126.

127.

128.

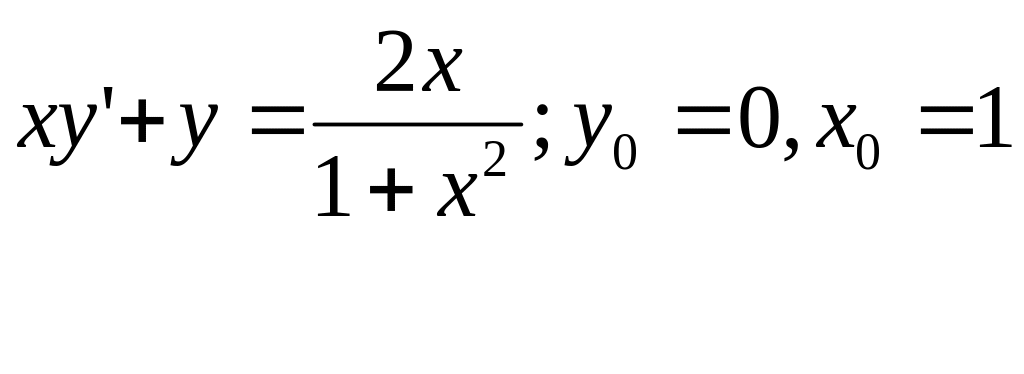
129.

130.

131-140. Найти общее решение дифференциального уравнения у" + ру' + gy = f(x)

и частное решение, удовлетворяющее начальным условиям

у = у0 при х = х0.

131.

132.

133.

134.

135.

136.

137.

138.

139.

140.

141-150. Написать три первых члена степенного ряда по заданному общему члену

; найти интервал сходимости ряда и исследовать его сходимость

на концах этого интервала.

141. 142. 143. 144.

145. 146. 147. 148.

149. 150.

151-155. Выразить определенный интеграл в виде сходящегося ряда,

используя ряд Маклорена для подынтегральной функции. Найти

приближенное значение этого интеграла с точностью до 0,001.

151. b = 0,2; k = 5. 152.b = 0,8; k = 1,25

153.b = 0,4; k = 2,5 154.b = 1,25; k = 4.

151. b = 0,5; k = 2.

156-160.Выразить определенный интеграл в виде сходящегося ряда,

используя ряд Маклорена для подынтегральной функции. Найти

приближенное значение этого интеграла с точностью до 0,001.

156. b = 0,4; k = 2,2. 157.b = 0,6; k = 0,4

158.b = 0,5; k = 0,9 159.b = 0,4; k = 1,7.

160. b = 0,6; k = 0,7.

161-170. Элементы комбинаторики. События и их вероятность. Классическое и

геометрическое определение вероятности. Формула Бернулли. Локальная

и интегральная теоремы Муавра – Лапласа.

161. На шести одинаковых карточках написаны буквы: В, А, О, С, М, К. Карточки

перемешиваются и раскладываются наугад в ряд. Какова вероятность того,

что при этом получится слово «Москва»?

162. Среди 40 деталей 3 нестандартные. Наудачу взяты 2 детали. Найти

вероятность того, что они нестандартные.

163. Найти вероятность того, что точка, брошенная в круг радиуса 1, окажется вне

вписанного в этот круг квадрата.

164. В урне 3 белых и 7 черных шаров. Какова вероятность того, что вынутые на

удачу два шара окажутся черными?

165. Среди 17 студентов группы, из которых 8 девушек, разыгрывается 7 билетов

в театр. Какова вероятность того, что среди обладателей билетов окажутся

4 девушки?

166. При наборе телефонного номера абонент забыл две последние цифры и

набрал их на удачу, помня только, что эти цифры нечетные. Найти

вероятность того, что номер набран правильно.

167. Из партии, в которой 30 деталей без дефекта и 5 с дефектом, берут наугад

три детали. Какова вероятность того, что среди них две детали без дефекта?

168. На каждой из шести карточек написана одна из следующих букв:

а, т, м, р, с, о. Карточки тщательно перемешиваются. Найти вероятность

того, что на четырех вынутых по одной и расположенных «в одну линию»

карточках можно будет прочесть слово трое.

169. Из карточек разрезанной азбуки составлено слово «вероятность», затем из 11

этих карточек по схеме случайного выбора без возвращения отобрано 6

карточек, которые разложены по мере их появления. Найти вероятность того,

что можно будет прочесть слово «ярость».

170. На плоскости начерчены две концентрические окружности, радиусы которых

5см и 7 см. Найти вероятность того, что точка, брошенная наудачу в большой

круг, попадет в кольцо, образованное построенными окружностями.

171 – 180. В первых двух пунктах (п. а и б) вычислить Рn (k)- вероятность

наступления события А ровно k раз в серии из n независимых

испытаний, если р – вероятность наступления этого события в одном

испытании; в третьем пункте (п. в) при тех же условиях найти

Рn (k1, k2 )- вероятность наступления события А не менее k1 раз и не

более k2 раз.

171. а) р = 0,7; k = 3; n = 5.

б) р = 0,01; k = 2; n = 500.

в) р = 0,3; k1 = 80; k2 = 90; n = 250.

172. а) р = 0,12; k = 45; n = 250.

б) р = 2/3; k = 2; n = 3.

в) р = 0,8; k1 = 200; k2 = 230; n = 30.

173. а) р = 0,25; k = 2; n = 4.

б) р = 0,003; k = 0; n = 100.

в) р = 0,15; k1 = 45; k2 = 70; n = 400.

174. а) р = 0,5; k = 2; n = 6.

б) р = 0,001; k = 5; n = 4000.

в) р = 0,32; k1 = 90; k2 = 100; n = 25.

175. а) р = 0,25; k = 75; n = 300.

б) р = 0,4; k =1; n = 5.

в) р = 0,55; k1 = 130; k2 = 200; n = 400.

176. а) р = 0,8; k = 3; n = 5.

б) р = 0,25; k = 85; n = 300.

в) р = 0,5; k1 = 300; k2 = 380; n = 800.

177. а) р = 0,2; k = 2; n = 6.

б) р = 0,01; k = 6; n = 200.

в) р = 0,25; k1 = 120; k2 = 230; n = 520.

178. а) р = 0,75; k = 170; n = 244.

б) р = 0,7; k = 2; n = 5.

в) р = 0,18; k1 = 55; k2 = 90; n = 250.

179. а) р = 0,2; k = 76; n = 330.

б) р = 0,01; k = 2; n = 500.

в) р = 0,3; k1 = 120; k2 = 210; n = 530.

180. а) р = 0,1; k = 1; n = 5.

б) р = 0,02; k = 4; n =200.

в) р = 0,6; k1 = 220; k2 = 235; n = 400.

Список рекомендуемой литературы.

1. Кудрявцев В.А., Демидович Б.П. «Краткий курс высшей математики.»

4-е изд. М., 1975.

2. Минорский В.П. «Сборник задач по высшей математике.»

3-12 изд.М.,1955-1977.

3. Ефимов Н.В. «Краткий курс аналитической геометрии.»

6-12 изд.М.,1962-1975.

4. Клетеник Д.В. «Сборник задач по аналитической геометрии.»

2-13 изд.М.,1954-1980.

5. Пискунов Н.С. «Дифференциальное и интегральное исчисление»

9-12 изд.М.,1970-1978, т.1,2.

6. Данко П.Е., Попов А.Г. «Высшая математика в упражнениях и задачах.»

М., 1998.

7. Гмурман В.Е. «Теория вероятностей и математическая статистика.»

М.,1998.

8. Гмурман В.Е. «Руководство к решению задач по теории вероятностей и

математической статистики.» М.,1998

Надежда Анверовна Андрюшечкина

Сергей Григорьевич Уфимцев

Анна Анатольевна Бабкина