2. Схематизация элементов технологических систем
[1] с.34-42
Для решения конкретных задач при большом разнообразии условий теплообмена в технологических системах прибегают к определенной схематизации процесса.
Реальные тела и источники (стоки) теплоты заменяют телами и источниками более простой формы, но похожими на реальные. Также схематизируют и условия взаимодействия тел с окружающей средой. Схематизация делается с целью облегчения математического описания процесса теплообмена в конкретных задачах.
2.1 Схематизация формы тел
Реальную конфигурацию тел, участвующих в теплообмене, приводят к одной из упрощенных форм. Каждая из форм кодируется (табл. 2.1)
Таблица 2.1 – Схематизированные формы тел
Форма тела |
код |
Форма тела |
код |
||
|
неограниченное пространство |
0 |
|
стержень неограниченный (любого сечения) |
4 |
|
полупространство |
1 |
|
стержень ограниченный с одной стороны |
5 |
|
пластина неограниченная |
2 |
|
стержень конечной длины |
6 |
|
пластина ограниченная (параллелепипед) |
3 |
|
цилиндр |
7 |
|
|
|
|
клин бесконечный |
8 |
|
|
|
|
шар |
9 |
Как влияет форма тела на процесс теплообмена? Влияние формы тела тем меньше, чем меньше размеры источника теплоты по отношению к размерам тела. Влияние формы тела тем меньше, чем короче период тепловыделения (времени действия источника теплоты).
На телах, участвующих в теплообмене, можно выделить пассивные граничные поверхности, температура которых изменяется незначительно, что мало влияет на температуру интересующей области. Пассивные граничные поверхности могут быть отодвинуты на любое расстояние, им можно придавать любую форму. Например, при плоском шлифовании толстой пластины (рис.2.1) можно нижнюю поверхность отодвинуть в бесконечность, т.е. вместо пластины (код3) рассматривать полупространство (код 1).
Рис. 2.1 – Схема плоского шлифования.
а – пассивная граничная поверхность.
Рис. 2.2 – Схема зоны стружкообразования
Лезвие инструмента (рис. 2.2) можно рассматривать как бесконечный клин (код 8), стружку – как стержень, ограниченный с одной стороны (код 5).
2.2 Схематизация источников и стоков теплоты
Разнообразие технологических систем и подсистем в машиностроении приводит к многообразию источников и стоков теплоты, возникающих в реальных процессах. Для систематизации решений задач теплообмена источники и стоки теплоты схематизируются по следующим признакам:
по мерности, т.е. по форме и размерам;
по виду закона распределения плотности тепловыделения;
по скорости перемещения;
по длительности функционирования.
Схематизация по мерности
Источники могут быть:
трехмерными, если тепловыделение распределено по объему тела. Эти источники имеют вид геометрических тел – параллелепипеда, цилиндра, шара и т.д.;
двумерными, если размер источника по одной из осей намного меньше, чем по двум другим. Этим размером можно пренебречь. Такие источники будут плоскими и иметь вид плоских фигур – прямоугольников, кругов, треугольников и др.;
одномерными, если размер источника по одной из осей намного превышает размеры по двум другим. Эти источники имеют вид отрезков линий – прямой, окружности и др.;
точечными, если размеры источника весьма малы по сравнению с размерами тела.
Схематизация по виду закона распределения плотности тепловыделения
Выделим в трехмерном
источнике тепловыделения точку М с
координатами
(индекс u – относится
к источнику). Если процесс теплообмена
установившийся, то элементарное
количество теплоты dQ
выделившейся за время τ в
элементарном объеме dV
будет равно
, (2.1)
где q – плотность тепловыделения в точке М.
Величина
зависит
для установившегося процесса от координат
точки М и имеет сложный вид.
Для удобства вычислений величину q можно представить следующим образом
, (2.2)
где q0 – максимальная плотность тепловыделения;
– функция, описывающая закон распределения
тепловыделения в объеме и являющаяся
безразмерной. Количество теплоты,
выделившейся в объеме V
за время τ определяем, интегрируя
выражение (2.1.)
Учитывая, что
,
имеем
Величины τ и q0 являются постоянными.
Тогда
Обозначим интеграл
В этом случае
(2.3.)
Функция U будет иметь вид:
для трехмерного источника
для двумерного источника
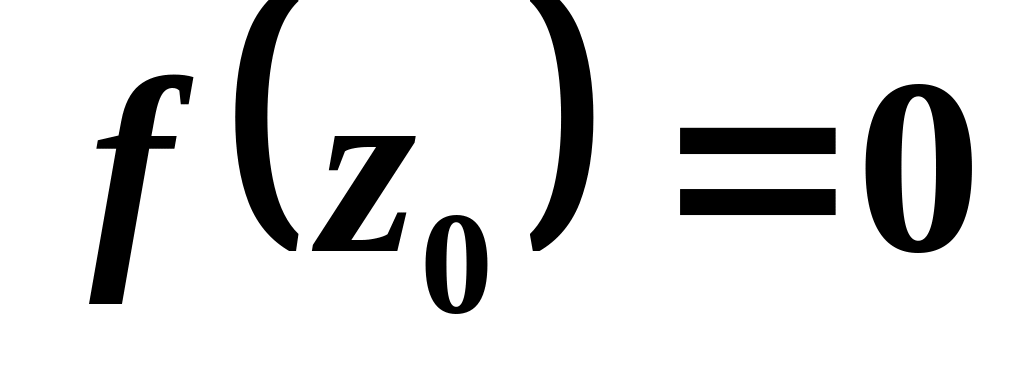
для одномерного источника
,
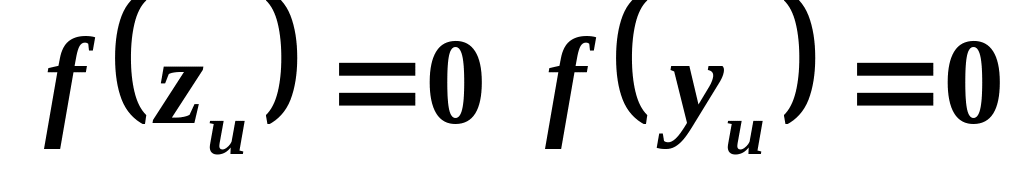Из формулы (2.3.)
(2.4)
где W – средняя мощность тепловыделения.
Максимальная плотность тепловыделения q0 имеет размерность:
для трехмерного источника Вт/м3
для двумерного источника Вт/м2
для одномерного источника Вт/м
для точечного источника Вт
Для действующих реальных источников теплоты вид зависимости достаточно сложен. Поэтому эту безразмерную функцию заменяют некоторой схематизированной.
Закон распределения плотности
тепловыделения может быть установлен
только вдоль одной оси, т.е. только для
одномерного источника
.
Двумерные и трехмерные источники представляют собой комбинации законов распределения по двум или трем осям.
Схематизированные законы распределения плотности тепловыделения источников приведены в таблице (2.2)
Таблица 2.2 – Законы распределения плотности тепловыделения.
код |
График закона распределения |
Закон |
Функция f(xu) |
1 |
|
Равномерно распределенный |
f(xu) = 1 |
2 |
|
Линейный |
f(xu) = 1 – ψu |
Продолжение таблицы 2.2
3 |
|
Линейный |
f(xu) = ψu |
4 |
|
Экспоненциальный |
f(xu) = exp[ - k0xu] |
5 |
|
Нормально распределенный несимметричный |
|
6 |
|
Нормально распределенный несимметричный |
f(xu) = exp[ – k0(l – xu)2] |
7 |
|
Нормально распределенный симметричный |
|
8 |
|
Комбинированный |
f(xu) = 1 f(xu) = exp[ – k0(ψu – 0,5)]
|
В этой таблице величины ψu и k0 – параметры распределения.
Код закона распределения плотности тепловыделения источника или стока теплоты содержит 3 цифры, т.е. определяет законы распределения по каждой из осей, что соответствует трехмерному источнику.
Для двумерных источников одна из цифр в коде будет нулем, т.к. по одной из осей распределения нет.
Если источник одномерный, то код содержит два нуля, т.к. распределение плотности тепловыделения будет только по одной оси.
Для точечного источника код содержит три нуля.
При решении теплофизических задач обычно известно количество выделившейся теплоты Q за время действия источника τ, т.е. известна тепловая мощность источника W. Требуется определить q0 – максимальную плотность тепловыделения для разных значений функции U, т.е. разных законов распределения.
В большинстве случаев при рассмотрении процессов теплообмена в элементах технологических систем, связанных с операциями механической обработки и металлорежущими станками, источники и стоки теплоты являются двумерными, т.е. представляют собой плоские фигуры. Рассмотрим некоторые примеры двумерных источников. В этом случае функция
Код распределения 101 – двумерный источник, равномерно распределенный вдоль двух осей (рис.2.3.)
Рис. 2.3 – Источник с кодом 101
По таблице (2.2.)
f(x) = 1, f(y) = 1
x изменяется от 0 до l,
y изменяется от 0 до b
,
откуда 
(2.5)
Код распределения 201 – двумерный источник распределен по линейному закону вдоль оси x и равномерно вдоль оси y (рис.2.4)
По таблице (2.2)
,
где
,
x изменяется от 0 до l,
y изменяется от 0 до b
;
(2.6)
Рис. 2.4 – Источник с кодом 201
Код распределения 501 – двумерный источник распределен по нормальному несимметричному закону по оси x и равномерно по оси y (рис.2.5)
По таблице
x изменяется от 0 до l,
y изменяется от 0 до b
,Интеграл
Рис. 2.5 – Источник с кодом 501
Интеграл
,
где
– интеграл вероятности, значения
которого табулированы (называется
«эрфект»). Таким образом
. (2.7)
Код распределения 801 – двумерный источник распределен по комбинированному закону по оси x и равномерно по оси y (рис.2.6)
После интегрирования получаем
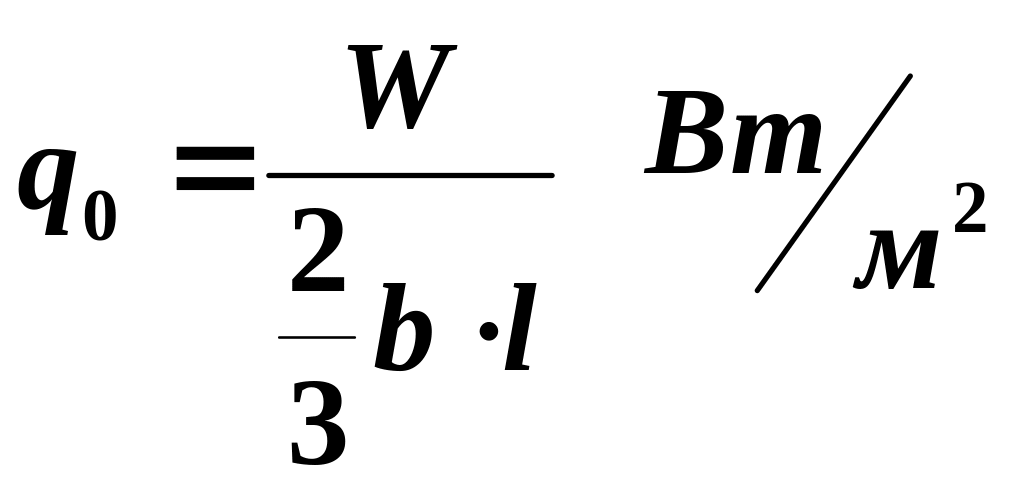(2.8)
Рис. 2.6 – Источник с кодом 801
Код распределения 101 – двумерный круговой источник с равномерным распределением (рис.2.7)
После интегрирования получаем
,
где R – радиус источника
(2.9)
Рис. 2.7 – Круговой источник с кодом 101
Код распределения 707 – двумерный круговой источник с нормальным законом распределения (рис.2.8)
После интегрирования получаем
,
где R – радиус пятна
нагрева
(2.10)
Рис. 2.8 – Источник с кодом 707
Аналогично рассчитывают величину q0 для источников с другими законами распределения.
Схематизация источников и стоков теплоты по скорости их перемещения
По скорости перемещения источники разделяются на неподвижные (V = 0), движущиеся (V > 0) и быстродвижущиеся (V > VT), т.е. такие, скорость движения которых больше скорости VT распространения теплоты в теле.
Для движущихся и быстродвижущихся источников рассчитывается безразмерный критерий Пекле
(2.11)
где V – скорость
перемещения источника,
;
l – длина источника в направлении перемещения, м;
ω – коэффициент температуропроводности
материала тела,
.
Физический смысл критерия Пекле – безразмерная скорость движения источника.
Если Pe < 10,то источник движущийся, если Pe ≥ 10, то источник быстродвижущийся.
Теплота в теле впереди быстродвижущегося источника не распространяется, а распространяется только под ним и за ним.
Схематизация источников и стоков теплоты по длительности функционирования
Длительность функционирования источника характеризуется безразмерным критерием Фурье
(2.12)
где ω – коэффициент
температуропроводности,
;
τ – время функционирования, с;
l – длина источника, м.
По длительности функционирования источники делятся на мгновенные ( при τ→0, F→0 ) ; действующие в течение некоторого конечного промежутка времени ( F0 > 0 ). При установившемся теплообмене τ→∞, F→∞.
Безразмерный критерий Фурье называется безразмерным временем.