1 Теплообмен в твердых телах

[1] c. 12-33

1.1 Температурное поле в твердом теле

Энергию частиц вещества в твердых в телах характеризует температура.

Совокупность температур в денный момент времени для всех точек твердого тела называют температурным полем.

В общем случае температура в любой точке твердого тела зависит от координат точки и времени

Q = f₃ (x, y, z,  ), (1.1)

где x,y,z – координаты точки,

 – время.

Эта формула выражает трехмерное температурное поле. На практике встречаются случаи, когда изменение температуры по одной или двум координатам незначительно и им можно пренебречь.

Например, если изменение температуры по координате z незначительно, то

,

формула(1.1) имеет вид

Q = f₂ (x,y,  ) (1.2)

и описывает двумерное температурное поле.

Аналогично, если изменение температуры по координатамz и y незначительно, то , и

Q = f₁ (x,  ), (1.3)

Формула (1.3) описывает одномерное температурное поле.

Если температура точек тела изменяется во времени, то температурное поле называется нестационарным, а тепловой режим неустановившимся.

Если температура точек тела не меняется во времени, т.е. , то поле называется стационарным, а тепловой режим – установившимся.

Для стационарного температурного поля и установившегося режима имеем

и Θ = f₃ (x, y, z), (1.4)

Θ = f₂ (x, y), (1.5)

Θ = f₁ (x), (1.6)

Формулы(1.4, 1.5, 1.6) описывают трехмерное, двумерное и одномерное стационарные температурные поля.

Если соединить все точки тела, имеющие одинаковую температуру, то получим изотермическую поверхность. Любая линия на этой поверхности является изотермой. Изотермические поверхности не могут пересекаться или иметь общие точки.

При переходе с одной изотермической поверхности на другую наблюдается изменение температуры.

Рассмотрим семейство изотерм, отличающихся друг от друга значениями температур на величину ΔΘ (рис. 1.1)

Рис. 1.1 – Семейство изотерм на плоскости

Скорость изменения температуры в точке А тела при переходе от одной изотермы к другой будет максимальной вдоль нормали (n). Эта скорость определяется отношением ΔΘ/Δn.

Скорость изменения температуры характеризуется градиентом температуры.

Градиентом температуры называется вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры. Он численно равен

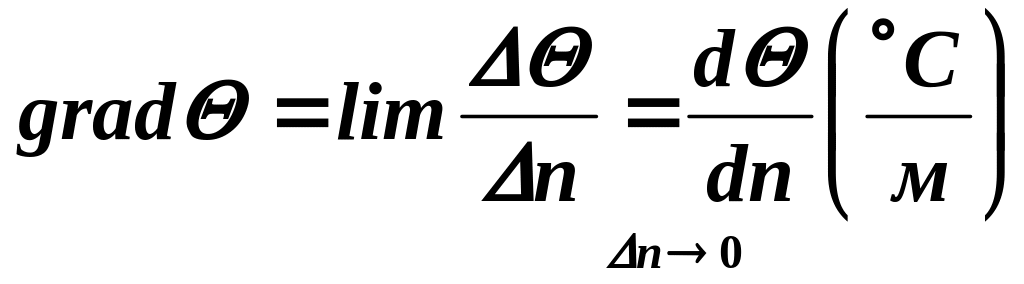(1.7)

и изображен на рис 1.1

Градиент температуры характеризует интенсивность изменения температуры внутри тела.

1.2 Основной закон теплопроводности. Закон Фурье.

Количество проходящей через тело теплоты называется тепловым потоком.

Закон Фурье в дифференциальной форме имеет вид

dQ = – ·grad·dF·d (1.8)

Элементарный тепловой поток dQ, проходящий через элемент поверхности dF (м²) за время d (с), пропорционален градиенту температуры grad (°С/м). В формуле (1.8) величина  – коэффициент пропорциональности. Тепловой поток dQ есть величина векторная. Знак “минус“ означает, что вектор теплового потока направлен с сторону, обратную вектору градиента температуры, т.е. тепловой поток направлен в сторону уменьшения температуры. (рис1.1)

Количество теплоты, проходящее через единицу площади в единицу времени, называется плотностью теплового потока:

(1.9)

Для стационарного температурного поля и установившегося режима определяется средняя плотность теплового потока

q = Q/F = W/F (Вт/м²), (1.10)

где W – мощность теплового потока, Вт.

Тепловой поток в этом случае определяется по формуле

Q = q·F· (Дж), (1.11)

Коэффициент пропорциональности  в формуле (1.8) называется коэффициентом теплопроводности материала, который является одной из теплофизических характеристик вещества.

Размерность коэффициента теплопроводности

 (Дж/м.с.°С = Вт/м.^оС)

Значения коэффициентов теплопроводности для различных материалов весьма различаются и приводятся в таблицах [1].Для примера приведем коэффициенты теплопроводности для некоторых веществ (Вт/м°С)

воздух  = 0.03

вода  = 0.60

сталь углеродистая  = 40.2

сталь нержавеющая  = 22,6

твердый сплав ВК  = 54,4

твердый сплав ТК  = 27,2

алмаз синтетический  = 520

медь  = 361