Нормально поле круглой петли.

При интерпретации результатов наблюдений по методу НП необходимо знать величины горизонтальной составляющей электрического и вертикальной составляющей магнитного полей, для круглой петли радиуса R, лежащей на поверхности однородного проводящего полупространства (z = 0) с волновым числом ϰ.

Внутри петли амплитуды E_φ и H_z с ростом |ϰ²R²| убывают медленнее, чем вне петли. Для малых значений |ϰ²R²| амплитуда электрического компонента растет пропорционально величине r/R (r – расстояние от центра петли до точки измерения).

Сдвиги фаз H_z и E_φ относительно тока J при заданном |ϰ²R²| меняется внутри петли весьма незначительно, а разность фаз составляющих E_φ и H_z для всех значений |ϰ²R²| близка к /2.

Вне петли разность фаз электрической и магнитной составляющих меняется в довольно широких пределах с изменением |ϰ²R²| и расстояния от петли.

При |ϰR| << 1 и р = | ϰr|  0 влияние проводящего пространства уменьшается и поле внутри петли стремится к полю в воздухе (или в высокоомных породах).

Амплитуды электрической и магнитной составляющих поля определяются в виде:

; . (82)

Импеданс поля выражается формулой:

. (83)

В центре петли при r = 0 электрическая составляющая поля равна 0, а магнитная составляющая поля определяется в виде:

. (84)

При малых и больших значениях р = |ϰr| можно пользоваться приближенными выражениями для магнитного числа h_z вертикальной компоненты магнитного поля:

Re h_z = 1- p³; Jm h_z = при р << 1; (85)

Re h_z = -2p²e^-pcos p; Jm h_z = при р >> 1; (86)

где h_z = - комплексная величина.

И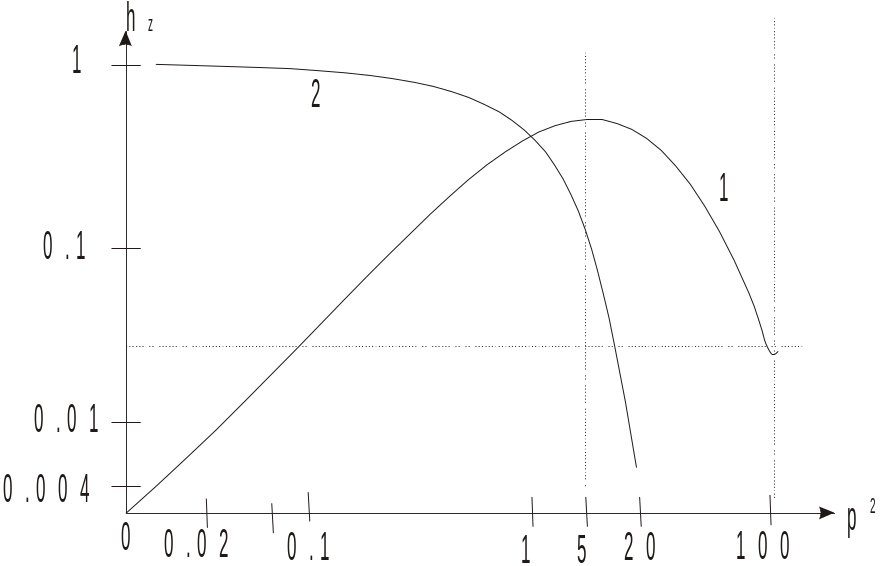 сходя из графиков действительной и мнимой части магнитного числа поля (рис. 1) видно, что в области малых значений р поглощение поля в нижнем проводящем полупространстве невелико и действительная часть h_z (кривая 2) стремится к единице, а мнимая часть h_z (кривая 1) растет пропорционально частоте. Мнимая составляющая магнитного числа имеет максимум при р = 5. В области больших значений р поглощение поля значительное и действительная часть h_z резко убывает до 0, а мнимая часть h_z стремится к 0 как монотонно.

Рис. 1.

Поле низкочастотного вертикального магнитного диполя.

Рассмотри поле низкочастотного вертикального магнитного диполя, расположенного на границе проводящего полупространства в цилиндрической системе координат, ось z которой совпадает с моментом диполя. Компоненты поля выражаются через электрические и магнитные числа e_i и h_i, соотношениями:

; , (87)

где m - магнитный момент диполя.

При малых приведенных параметрах р = |ϰr| << 1 электрические м магнитные числа равны:

e_zφ = 1 - p³ + i( - p³) + 0(p⁴), (88)

h_zz = 1 + p³ + i( - p³) + 0(p⁴). (89)

Первый индекс у измеряемого числа показывает направление диполя (z), а второй – измеряемого компонента (φ или z).

При р >> 1 имеем следующие асимптотические выражения:

e_zφ = i , h_zz = i . (90)

На основе приведенных формул легко найти выражения для амплитуд и фаз компонентов поля. Основные закономерности поля вертикального магнитного диполя следующие. При весьма малых р = |ϰr| << 1 магнитные числа е_φ и h_z компонент поля диполя ведут себя так же как в однородном пространстве. Отличие от этого поля проявляется, прежде всего, в действительной части e_φ и мнимой части h_z. В присутствии проводящего полупространства появляется новый компонент поля h_r, сдвинутый по фазе в ближней зоне на /2 относительно тока в источнике и растущий пропорционально частоте (рис. 2). Вследствие наличия фазового сдвига между магнитными числами h_z и h_r компонент магнитного поля, оно становится эллиптически поляризованным в меридиональной плоскости, проходящей через ось диполя (рис. 3).

Магнитные числа а^* и b^* полуосей эллипса поляризации вводятся соотношениями:

, . (91)

При больших параметрах р >> 1 электрическое поле не зависит от частоты и убывает обратно пропорционально четвертой степени расстояния. Магнитное поле имеет в основном радиальный компонент Н_r, убывающий с такой же скоростью и имеющий постоянный фазовый сдвиг (/4) относительно тока в диполе. Эллипс поляризации магнитного поля по мере удаления от диполя постепенно наклоняется и в зоне больших параметров поле почти линейно поляризовано и горизонтально (рис. 4).

Рис. 2, 3. Нормальное поле низкочастотного вертикального магнитного диполя (координатные компоненты).

Рис. 4. Нормальное поле низкочастотного вертикального магнитного диполя (элементы эллипса поляризации).