
- •Индуктивная электроразведка ( 8 семестр бакалавриат лекции 2015 по лекциям и.В. Притыки)
- •Общие сведения
- •Структура гармонического электромагнитного поля.
- •Элементы теории электромагнитного поля.
- •Основные уравнения электродинамики.
- •Система уравнений Максвелла.
- •Физический смысл уравнений Максвелла.
- •4. Материальные параметры γ, ε, μ.
- •Решение уравнений Максвелла для установившегося переменного электромагнитного поля.
- •Физический и геологический смысл волнового числа .
- •Метод незаземленной петли (нп).
- •Нормально поле круглой петли.
- •Поле низкочастотного вертикального магнитного диполя.
- •Горизонтальный магнитный диполь.
- •Круговой цилиндрический проводник в поперечном магнитном поле.
- •Определение параметра α по частотным характеристикам вторичного поля.
- •Решение обратной задачи для цилиндрического и сферического проводников.
- •Метод длинного кабеля (дк)
- •Нормальное поле бесконечно длинного кабеля.
- •Поле кабеля конечной длины
- •Интерпретация результатов наблюдений в методе дк.
- •Метод дипольного электромагнитного электропрофилирования.
- •Методика полевых работ методом дэмп.
- •Интерпретация результатов методом дэмп.
- •Метод индукции.
- •Горизонтальный магнитный диполь (вертикальная рамка).
- •Вертикальный магнитный диполь.
- •Наклонный магнитный диполь.
- •Методика полевых работ методом индукции.
- •Интерпретация результатов полевых измерений в методе индукции.
- •Метод радиокип (радиоволновое профилирование).
- •Методика и техника работ метом радиокип.
- •Помехи при полевых измерениях.
- •Обработка и интерпретация результатов наблюдений методом радиокип.
- •Методика и техника полевых работ.
- •Теоретические основы вгип.
- •Метод бесконечно длинного кабеля в аэроварианте.
- •Метод переходных процессов.
- •Площадная поисковая съемка.
- •Детальные работы мпп.
- •Интерпретация полевых материалов мпп.
- •О представлении результатов наблюдений в индуктивных методах в виде ρк.
- •Дипольное индуктивное профилирование (дип)
- •Метод длинного кабеля
- •Метод переходных процессов
- •Методика полевых работ
- •Обработка и интерпретация результатов полевых наблюдений
Основные уравнения электродинамики.
Электрический поток N0 через замкнутую поверхность равен
суммарному заряду «е» внутри этой поверхности, т.е.
N0 = 4πe. (8)
Магнитное напряжение F (магнитодвижущая сила) контура L
равно сумме быстроты изменения электрического потока N0 и полного тока проводимости J, пронизывающих поверхность данного контура, т.е.
F
=
![]() .
(9)
.
(9)
Магнитный поток сквозь замкнутую поверхность S всегда
равен 0, т.е.
Ф = 0. (10)
Электрическое напряжение ε (ЭДС) контура L равно быстроте
изменения магнитного потока Ф, пронизывающего поверхность данного контура (закон Фарадея), т.е.
ε
= -![]() .
(11)
.
(11)
Система уравнений Максвелла.
Фундаментальные законы и основные уравнения электродинамики позволили Максвеллу, после выполнения необходимых математических операций, вывести систему общих электромагнитных уравнений для любой непрерывной, неподвижной среды, связанной жестко с Землей (при отсутствии сторонних токов и сторонних зарядов).
К ним относятся:
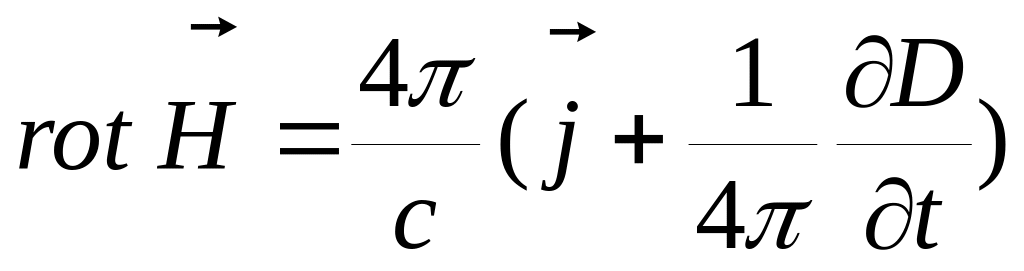 (12)
– 1 уравнение Максвелла.
(12)
– 1 уравнение Максвелла. (13)
– 2 уравнение Максвелла.
(13)
– 2 уравнение Максвелла.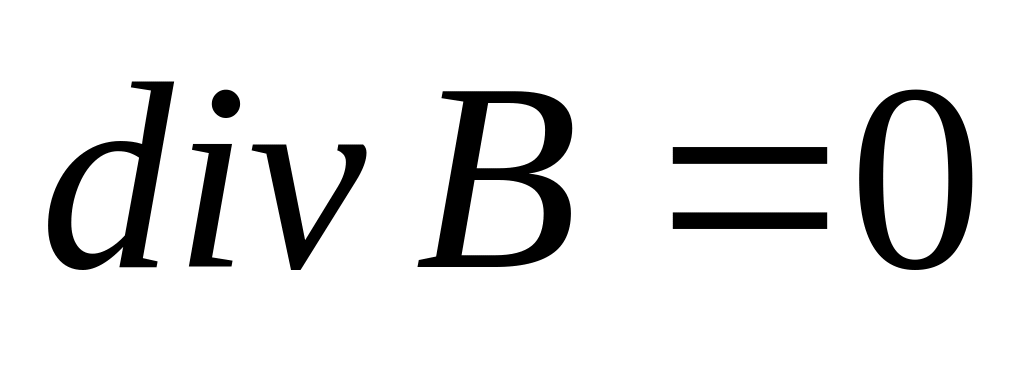 (14)
– 3 уравнение Максвелла.
(14)
– 3 уравнение Максвелла.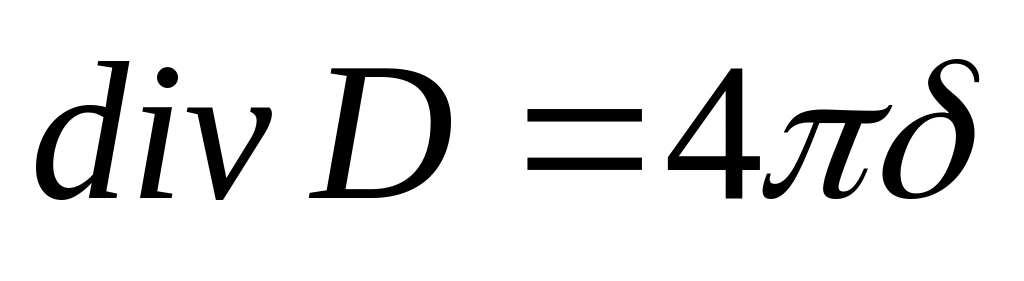 15)
– 4 уравнение Максвелла.
15)
– 4 уравнение Максвелла.
Приведенные уравнения Максвелла не содержат электромагнитных параметров среды и описывают универсальные свойства электромагнитного поля, объективно существующего в данной среде.
В данных формулах:
- вектор напряженности магнитного поля;
![]() -
вектор напряженности электрического
поля;
-
вектор напряженности электрического
поля;
![]() -
вектор электрической индукции
(электрическое смещение);
-
вектор электрической индукции
(электрическое смещение);
![]() -
вектор магнитной индукции;
-
вектор магнитной индукции;
![]() -
вектор плотности токов проводимости;
-
вектор плотности токов проводимости;
δ – плотность электрических зарядов.
Эта система уравнений не может быть решена однозначно, так как содержит пять неизвестных векторов , , , , при системе из четырех уравнений.
Для того, чтобы определить электромагнитное поле в конкретной среде, необходимо воспользоваться связями между векторами и , и , и вида:
= ε , = μ , = γ , (16)
где γ, ε, μ есть соответственно, электропроводность, диэлектрическая проницаемость и магнитная проницаемость среды. Материальные параметры γ, ε, μ для изотропной среды являются скалярными величинами и характеризуют электромагнитные свойства среды.
В формулах связи (16) параметры γ, ε, μ могут быть постоянные величинами или в виде функций от компонент поля (при интенсивных полях), от частот (при сверхнизких и сверхвысоких частотах) и от времени (при неустановившихся процессах).
В однородно – изотропной среде увеличение значение ε уменьшает напряженность электрического поля , а увеличение значения μ повышает магнитную индукцию среды.
