Методика полевых работ методом дэмп.

При проведении полевых работ по методу ДЭМП питающая и измерительная установки перемещаются по профилям как единое целое, сохраняя неизменным расстояние между собой r.

Шаг установки по профилю обычно составляет целую часть разноса r.

Сеть наблюдений и рабочая частота выбираются аналогично тому как это делается в методе НП. Наблюдение поля производится либо по методике абсолютных измерений Н_z с аппаратурой ДЭМП, либо по методике ЭПП (рис. 23).

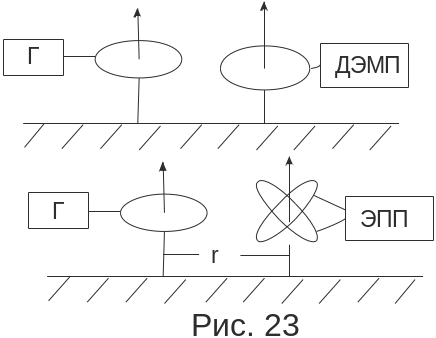
Методом ДЭМП решают 2 задачи:

1. Поиск проводящих объектов. Кроме Н_z могут измеряться

(более часто) составляющие эллипса поляризации. Методика ЭПП обеспечивает большую глубинность. Разнос r должен быть в 1.5 – 2 раза больше глубины залегания тела. При детализации снимается частотная характеристика аномалий, выявляется более детально структура поля, сгущается сеть, измерения ведутся с различными разносами r.

2. Картировочные работы. Ведутся только методом ЭПП.

Разнос r должен в 2 – 3 раза превышать глубину исследований. Рабочая частота выбирается по графику нормального поля магнитного числа малой полуоси b эллипса поляризации.

Нижний предел  зависит от точности измерения поля. Если породы сильно дифференцированы по , то можно измерять на разных участках планшета при разных рабочих частотах.

Целесообразно комплексировать метод ДЭМП с другими геофизическими методами.

Интерпретация результатов методом дэмп.

Особенностью интерпретации результатов дипольных измерений является необходимость учета разноса r применяемой установки, так как аномалии магнитного типа зависят от r.

Влияние разноса на аномалии магнитного типа проявляется двояко.

1. По данным моделирования установлено, что частотные

характеристики и амплитудно-фазовые соотношения аномалий определяются не только физическими свойствами и размерами аномального объекта, но и разносами установки. Для крутопадающих, вытянутых по простиранию и падению проводников разнос непосредственно входит в выражение параметра: α = rm (m – толщина эквивалентной пластины). Разнос r должен существенно превышать глубину залегания верхней кромки пластины. Для проводников с изометрическим сечением зависимость параметра α от разноса проявляется слабо и в первом приближении сохраняет тот же вид, что и в методе НП для шара. При интерпретации аномалий от изометрических объектов проводник заменяется эквивалентным шаром. Интерпретация базируется на анализе графика Н_z

2. От разноса установки существенно зависит форма и величина

аномалии.

Схема интерпретации аномалий от изометрических проводников.

В этом случае проводник заменяется шаром и интерпретация базируется на анализе графиков Н_z.

Рассмотрим вторичное магнитное поле идеально проводящей сферы в непроводящей среде (₂ = 0). Пусть оси генераторного и приемного диполей лежат в одной плоскости УОZ, проходящей через центр сферы, Р – точка наблюдения, О^/ - место положения генератора. Обычно их высота одинаковая, т.е. h = h₁ (рис. 24).

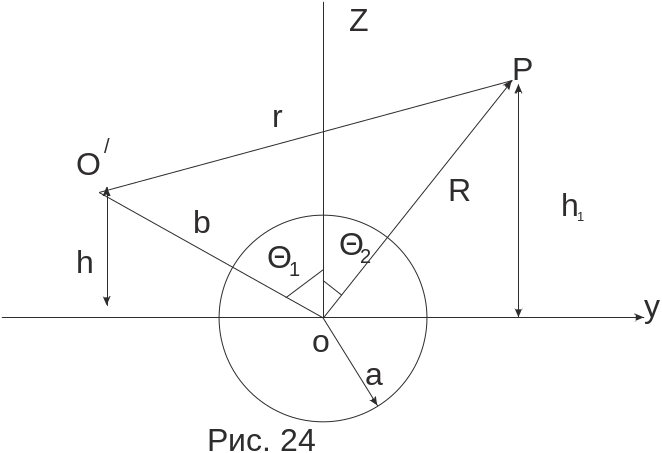
Вторичное магнитное поле сферы в этом случае удобно представить в виде произведения состоящего из трех сомножителей:

Н_вт = Н₀·F(|H_вт|, )·f(₁, ₂, R, b, r), (117)

где Н₀ – первичное поле магнитного диполя в точке наблюдения Р равно (т.к. H_i = , то Н₀ = ; (118)

F(|H_вт|, ) = - (119) величина и частотная характеристика вторичного поля:

f(₁, ₂, R, b, r) – функция зависящая от взаимного расположения приемного и генераторного диполей и центра сферы. Именно этот сомножитель (f) полностью определяет вид графиков любых компонентов поля по профилю, проходящему через центр сферы. В частности, когда генераторный и приемный диполи вертикальны имеем:

f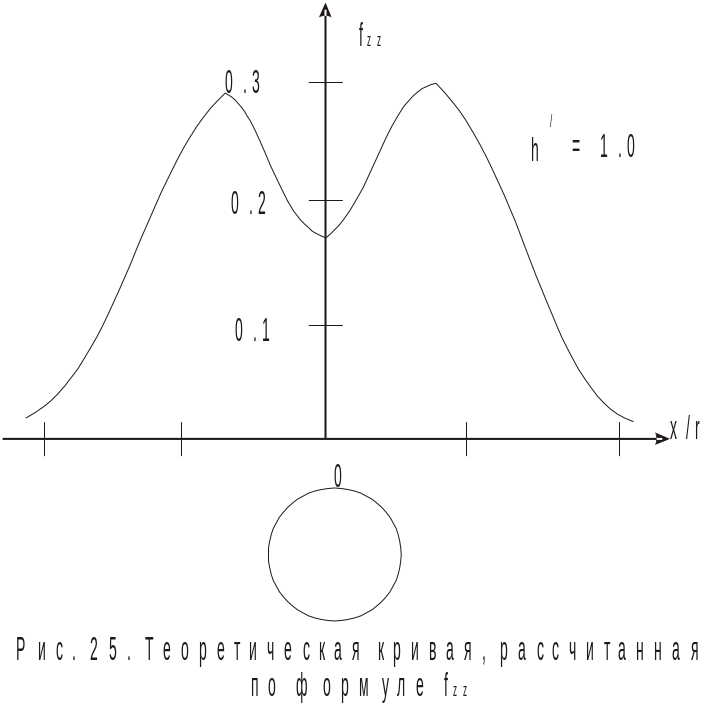 _zz = - [cos (₁ + ₂)·(2cos ₁·cos ₂ - sin ₁·sin ₂) – sin² (₁ + ₂). (120)

Над центром сферы наблюдается минимум, сопровождаемый двумя максимумами.

Выведены формулы и для f_zy (генераторный диполь вертикальный, а приемный диполь горизонтальный), f_yz, f_yy.

h^/ = - кривые индексированы отношением глубины залегания сферы к радиусу установки. По оси абсциcc x^/ = , где х – расстояние от эпицентра сферы, выраженное в разносе установки. Точка записи кривых отнесена к середине между генератором и приемником.

При больших значениях h^/ - аномалии H_zz и H_zy характеризуются наличием положительных экстремумов. При уменьшении глубины форма кривых усложняется, на них уже можно выделить участки, соответствующие моментам прохождения над шаром приемной и генераторной установок.

По данным детализации аномального участка находится профиль с максимальной аномалией, проходящий через эпицентр залежи, положение которого определяется по точке симметрии графика H_z. Глубина до центра эквивалентного шара находится по формуле:

, (121)

где Δх – расстояние между точками, где наблюдаются резкие экстремумы поля Н_z.

На основе многочастотных измерений поля Н_z определяется аномальный параметр α, а затем приведенный параметр аномалии τ = · , (122)

где d – диаметр шара.

После этого, с помощью теоретического графика для D находят функцию |D| или |H_вт| или Re Н_вт или Im Н_вт на той частоте, на которой производились детализационные исследования с разными разносами r. Затем по максимальной аномалии |H_вт|, полученной при наибольшем разносе r и по формуле: (123)

с учетом значения D вычисляется радиус эквивалентного шара а. Затем из выражения для τ, зная величину радиуса, определяем проводимость аномального объекта  (полагая  = 4·10^-7 Гн/м).

В методе ДЭМП при интерпретации аномалий от тел вытянутых по падению и простиранию (пластины) определяют глубину залегания их верхней кромки (h) и продольную проводимость пластины S = ·m. (124)

Критерием отношения тела к этому классу служит помимо формы аномалии линейная зависимость приведенного параметра аномалии τ от разноса.

Величина h находится по формуле:

, (125)

где Δх – расстояние между положительными экстремумами аномалии на графике Н_z.

Продольная проводимость тела находится по формуле:

τ = ··m·r = ·S·r. (126)

При использовании эллиптически поляризованного магнитного поля (а в методе ДЭМП очень часто интерпретируют данные измерений b и а или ) для вычисления _к пользуются палеткой нормального поля. Если измерять малую полуось b или горизонтальный компонент магнитного поля Н_а^Г, то

_к = = = (127)

Эта формула применяется в зоне малых параметров α.

По значениям _к, вычисленным в каждой точке, строится карта изолиний _к по участку работ, которая и подвергается дальнейшему геологическому истолкованию.

При интерпретации материалов приходится сталкиваться с одной из сложностей, которая заключается в том, что составляющие переменного магнитного поля вертикального магнитного диполя в случае сложного рельефа могут сильно искажаться, тогда как вся теория рассматривается для плоской границы раздела Земля – воздух.

Это приводит к значительным погрешностям в определении величины ρ_эф. Задача в общем виде для поля диполя на неровной поверхности проводящего полупространства математически не решается. Пока исследователями оценено только влияние на поле диполя рельефа в виде наклонной плоскости.

Исследования и расчеты показали, что при использовании поля вертикального магнитного диполя необходимо вводить поправки за рельеф дневной поверхности. Наиболее просто поправка может быть введена в результаты измерения угла наклона большой оси эллипса поляризации вектора магнитного поля к горизонту ψ, т.е. угола наклона вектора магнитного поля к горизонту.

В последнее время рассчитаны поправки за угол наклона дневной поверхности для следующих компонент поля вертикального магнитного диполя: |h_z|, |h_r|, , φ_hz, φ_hr,_, α и ψ.