
Основы проектирования РН Куренков
.pdf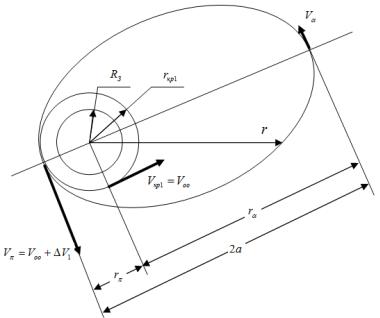
Рис. 6.3. Схема перевода КА на эллиптическую орбиту
6.1.6. Расчет приращения скорости для перевода КА с эллиптической орбиты на высокую круговую орбиту
Расчет, так же как и в предыдущем случае, производится с использованием той же зависимости (6.5) и учетом того, что приращение скорости происходит мгновенно в точке апогея эллиптической орбиты (см. схему, представленную на рис. 6.4).
Искомая добавка скорости определяется как разность между скоростью КА на высокой круговой орбите и скоростью КА в точке апогея эллиптической орбиты.
Пример 5. Определить приращение скорости V2 , которая не-
обходима для перевода КА с эллиптической орбиты на высокую круговую орбиту. Параметры орбит принять такими же, как в примере 4.
Решение. Рассчитаем сначала скорость полета КА по эллиптической орбите в точке апогея. При этом воспользуемся данными, полученными в примере 4:
121
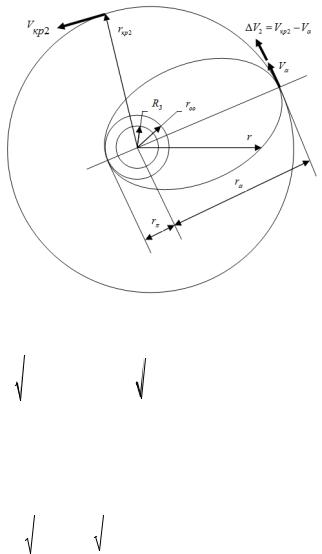
Рис. 6.4 Схема перевода КА с эллиптической орбиты на высокую круговую орбиту
V V1 |
|
2 |
|
1 |
|
7,91 |
|
|
|
2 |
|
1 |
|
1,597 [км/с]. |
RЗ |
|
|
|
6371 |
|
|
|
|
||||||
|
|
|
|
|||||||||||
|
r |
|
a |
|
|
|
|
42157 |
|
24364 |
|
|
||
Теперь рассчитаем скорость КА на высокой круговой орбите с высотой, соответствующей радиусу апогея эллиптической орбиты.
Расчетная формула будет практически такой же, как и формула (6.7), с той лишь разницей, что вместо радиуса опорной орбиты необходимо подставлять радиус высокой круговой орбиты. Таким образом можно получить следующие результаты:
V |
V |
|
RЗ |
|
7,91 |
|
6371 |
|
3,075 [км/с]. |
|
|
||||||||
кр2 |
1 |
|
r |
42157 |
|
||||
|
|
|
|
||||||
Тогда приращение скорости V2 , которая необходима для пере-
вода КА на высокую круговую орбиту в точке апогея эллиптической орбиты, будет следующим:
V2 Vкр2 V 3,075 1,597 1,478 [км/с].
122
6.1.7. Расчет приращения скоростей для перевода КА
свысокой круговой орбиты на эллиптическую орбиту
ис эллиптической орбиты на низкую круговую орбиту
Такого рода маневры используются, например, при перестроении орбитальной группировки космических аппаратов, перед спуском КА, а также для "захоронения" (затопления) отработавших КА.
Расчет приращений скорости проводится в той же последовательности, что и расчет скорости для перевода КА на высокие орбиты. Но при этом следует учитывать, что процесс перехода осуществляется в обратной последовательности и что в соответствующих точках орбиты скорость нужно гасить, а не добавлять (то есть КА необходимо тормозить до необходимой скорости).
6.1.8. Расчет приращения скорости для изменения плоскости орбиты
Необходимость в изменении плоскости орбиты возникает, например, при запуске КА на геостационарную орбиту с космодромов, которые располагаются не на экваторе. Изменять плоскость орбиты также приходится в тех случаях, когда вывод КА непосредственно на рабочую орбиту с заданным наклонением невозможен из-за ограничений по азимутам пуска РН. Такие ограничения существуют для каждого конкретного космодрома и связаны в основном с освоенными трассами и согласованными районами падения отработавших ракетных блоков.
V2
V3
V1
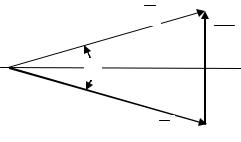
Рис. 6.5. Схема для расчета приращения
скорости КА для изменения плоскости орбиты
Поворот плоскости орбиты проводится путем изменения направления вектора скорости КА. Для этого необходимо сообщить КА приращение импульса скорости. Расчётная схема для изменения плоскости орбиты на угол приведена на рис.
6.5.
123
На этой схеме V1 - первоначальный вектор скорости КА, V2 - вектор скорости КА после изменения плоскости орбиты на угол .
Из схемы видно, что для изменения направления вектора скорости V1 на угол (чтобы получить вектор скорости V2 ) необходимо доба-
вить вектор скорости V3 .
Из геометрических соотношений нетрудно получить модуль век-
тора V3 : |
|
V3 2 V1 sin 2 . |
(6.12) |
Пример 6. Пусть необходимо изменить плоскость орбиты на 60°. Тогда по формуле (6.12) получаем
V |
2V sin |
60 |
V . |
|
|||
3 |
1 |
2 |
1 |
|
|
|
Из примера видно, что для поворота плоскости орбиты КА на 60 градусов необходимо сообщить КА импульс скорости, равной скорости полета КА на первоначальной орбите.
Для спутников, запускаемых с космодрома Байконур с углом наклона плоскости орбиты 51,6 градусов, приращение скорости для перевода КА в плоскость экватора составит
V |
2V sin |
51,6 |
0,87 V . |
|
|||
3 |
1 |
2 |
1 |
|
|
|
Поэтому запуск КА на орбиты, лежащие в плоскости экватора, выгоднее производить с космодромов, находящихся на экваторе.
Следует также отметить, что для изменения плоскости орбиты выгоднее всего сообщать космическому аппарату импульс скорости в точке апогея орбиты, так как в этой точке скорость КА минимальна.
На рис. 6.6 приведена расчётная схема вывода КА на геостационарную орбиту с космодромов Байконур и Плесецк.
Изменение угла наклона плоскости орбиты при запуске КА на геостационарную орбиту проводится, как правило, с использованием в структуре ракеты-носителя разгонного блока.
Вывод осуществляется в следующей последовательности. Комплекс КА с разгонным блоком выводится на опорную круговую орбиту 1 с углом наклонения i. Осуществляется приращение импуль-
124
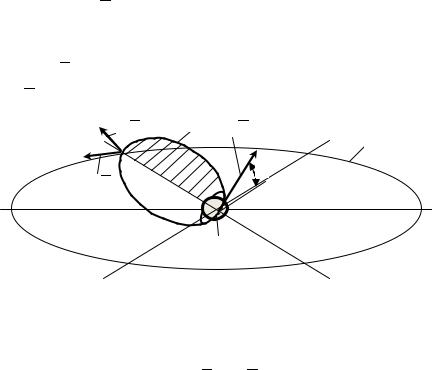
са скорости V1 и полёт продолжается по эллиптической (геопере-
ходной) орбите 2. Вблизи апогея геопереходной орбиты осуществляется поворот её плоскости на угол i за счёт приращения вектора ско-
рости V3 , затем осуществляется переход на стационарную орбиту
( V2 ), где КА отделяется от разгонного блока.
V3 |
2 |
V1 |
|
|
3 |
||
|
|
|
i
V2
1
Рис. 6.6. Расчётная схема вывода КА на геостационарную орбиту
Практически вывод на геопереходную орбиту осуществляется через несколько промежуточных эллиптических орбит, а для реали-
зации приращений скорости V3 и V2 двигатель разгонного блока
включается один раз с обеспечением управления необходимого пространственного маневра.
На рис. 6.7 приведена одна из реальных схем вывода ПН на ГСО. Она отличается наличием промежуточных орбит для обеспечения необходимой точности выведения. Однако вопросы точности решаются на последующих этапах проектирования и для проектных расчётов можно пользоваться схемой вывода, показанной на рис. 6.6, тем более что потребные характеристические скорости для этих двух схем отличаются незначительно.
Пример 7. Определить характеристическую скорость ракетыносителя с разгонным блоком для запуска КА на стационарную орбиту. Угол наклона плоскости опорной орбиты принять равным 51,6 градусов.
125
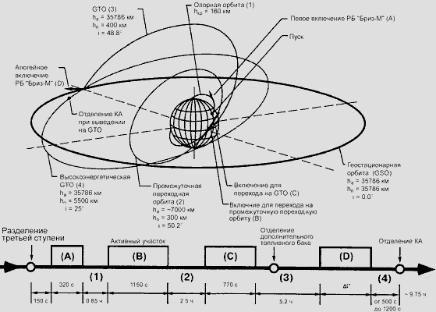
Рис. 6.7. Реальная схема вывода КА на геостационарную орбиту
Решение. Приращения скорости для проведения маневров в нашем примере уже известны, поскольку параметры промежуточных орбит совпадают с параметрами, приведенными в примерах 1 - 6:
n
VXпотр VXпотрид VG VA VR Vi i 1
8,029 1,35 2,46 0,87 1,597 1,478 14,706 [км/с].
Здесь из выражения (6.2) использовалась скорость, соответствующая нижней границе потерь скорости.
При некоторых схемах запуска предусматривается, что разгонный блок осуществляет старт с опорной орбиты на геопереходную и поворот плоскости орбиты, а последний маневр - перевод КА на стационарную орбиту - осуществляется двигателями самого КА. Это обстоятельство необходимо учитывать при расчёте потребной характеристической скорости РН.
126

6.2.Старт к Луне и планетам
6.2.1.Старт к Луне
Вобщем случае задачу определения параметров движения КА к Луне следует решать при наличии двух притягивающих центров, Земли и Луны. Для проектных расчетов в первом приближении можно считать, что Луна не притягивает КА. Расчет в этом случае сводится к схеме перехода КА с опорной орбиты на эллиптическую (очень вытянутую). Радиус апогея такой орбиты равен расстоянию от Земли до Луны, то есть примерно 384400 км. При этом в действительности будет некоторый запас характеристической скорости, так как Луна притягивает КА.
Ограничимся случаем, когда перелёт к Луне осуществляется не в плоскости орбиты Луны, а в плоскости опорной орбиты, то есть поворот плоскости орбиты КА не требуется. При этом необходимо подобрать время старта таким, чтобы плоскость опорной орбиты проходила вблизи точки будущей «встречи» космического аппарата и Луны.
Пример 8. Определить приращение скорости, необходимой для старта космического комплекса к Луне с опорной орбиты.
Решение. Линейная скорость КА на круговой опорной орбите (орбите ожидания) высотой 200 км, как было показано ранее (см. пример 2), составляет 7,79 км/с.
Радиус апогея эллиптической орбиты принимаем равным среднему расстоянию от Земли до Луны, то есть r = 384400 км.
Рассчитаем большую полуось эллиптической орбиты:
a |
r r |
|
6571 384400 |
195485 км. |
|
|
|
|
|||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Скорость в перигее орбиты рассчитывается по формуле (6.5): |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V VI |
|
2 |
|
1 |
7,91 |
|
|
2 |
|
|
1 |
|
10,923 [км/с]. |
||||||
RЗ |
|
|
|
6371 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
r |
|
a |
|
|
|
|
|
6571 |
|
195485 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
127 |
Следовательно, при отлете с орбиты ожидания к Луне космическому аппарату требуется приращение скорости:
V1 V Voo 10,923 7,789 3,134 км/с.
6.2.2. Старт к планетам
Будем полагать, что плоскости всех орбит совпадают и планеты движутся по круговым орбитам, а радиусы орбит планет равны среднему расстоянию от Солнца до соответствующей планеты. Такое упрощение задачи для первого приближения вполне допустимо, ибо эксцентриситеты планетных орбит и их наклонения к плоскости земной орбиты небольшие.
Прежде всего отметим, что плоскость орбиты менять не нужно даже при запуске с космодромов, расположенных далеко от экватора. Просто следует подобрать время старта ракеты-носителя таким, чтобы плоскость опорной орбиты была определенным образом ориентирована относительно Солнца, а момент старта с опорной орбиты таким, чтобы гиперболическая отлетная траектория на границе гравитационного действия Земли совпадала с вектором скорости межпланетного КА был параллелен вектору скорости орбитального движения Земли вокруг Солнца.
Упрощенная схема, поясняющая относительное расположение орбит Земли (вокруг Солнца) и КА (вокруг Земли) в момент старта межпланетного комплекса с опорной неэкваториальной орбиты без поворота плоскости орбиты, показана на рис. 6.8. На этом рисунке введены следующие обозначения: 1 – Солнце; 2 – Земля; 3 – орбита старта; 4 – центр Земли; 5 - межпланетные комплексы; 6 – касательная к орбите Земли; 7 – орбита Земли (вокруг Солнца); 8 – линия «Земля-Солнце»; 9 и 10 – гиперболические отлётные траектории к внешним и внутренним планетам соответственно.
Двигатели ракетного блока, предназначенного для старта с опорной орбиты к планетам, должны включаться вблизи точек перигея гиперболических отлётных траекторий с асимптотами, параллельными с касательной (6). Тогда перелет будет осуществляться вблизи плоскости орбит планет. Отметим. Что если задачу не упрощать, то отлетная траектория - сложная пространственная кривая, на которую оказывают влияние сила притяжения Земли, сила тяги и
128
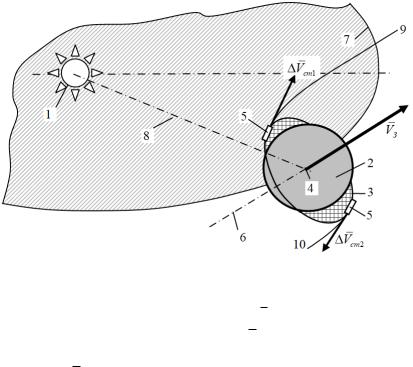
время работы двигательной установки межпланетного комплекса и др. Но это задача динамики полёта и здесь не рассматривается.
Рис. 6.8. Схема относительного расположения орбит Земли и КА в момент старта межпланетного комплекса
Если вектор приращения скорости ( Vст1 ) совпадает с вектором
скорости Земли относительно Солнца VЗ , то возможен перелет к внешним планетам (Марс, Юпитер и т.д.). Если вектор приращения скорости ( Vст2 ) направлен в противоположном направлении, то возможен перелет к внутренним планетам (Венера, Меркурий).
Методику расчета характеристической скорости рассмотрим на примере старта к Марсу.
Характеристическая скорость для перевода КА с опорной земной орбиты на межпланетную траекторию без учета притяжения Земли
Наиболее рациональной схемой межпланетных полетов считается гомановский переход космического аппарата с орбиты Земли на орбиту Марса (рис. 6.9).
Если не учитывать притяжения планеты отлета и планеты назначения, а ограничиться только действием сил притяжения Солнца, то
129
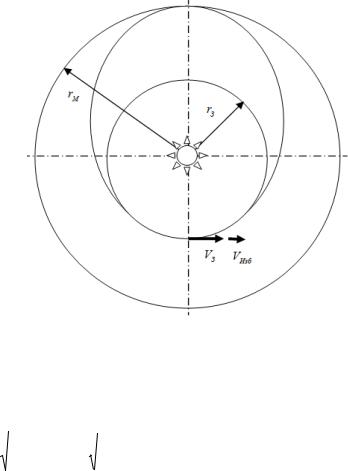
схемы расчета межпланетных траекторий будут полностью совпадать со схемами расчетов при переходе искусственного спутника Земли с одной круговой орбиты на другую, лежащую в той же плоскости. Необходимо лишь вместо геоцентрических данных подставить гелиоцентрические.
Исходные данные для решения этой задачи следующие:
-гравитационная постоянная Солнца 1,32·1020 м3 /с2 ;
-среднее расстояние от Солнца до Земли 1,496·1011 м;
-среднее расстояние от Солнца до Марса 2,278·1011 м.
Рис. 6.9. Гомановский переход с орбиты Земли на орбиту Марса
Рассчитывается полуось эллиптической межпланетной орбиты:
|
r |
r |
|
1,496 1011 2,278 1011 |
|
|
a |
|
|
|
|
1,887 1011 |
м , |
|
2 |
2 |
||||
|
|
|
|
|
||
а затем скорость КА в точке перигелия межпланетной орбиты:
|
|
2 |
|
1 |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
c |
|
|
|
|
11 |
11 |
|
||||||||||
V |
|
|
|
|
|
|
|
1.32 |
|
1020 |
|
|
|
|
|
32725 м / с . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
r |
|
a |
|
|
|
|
1.496 10 |
|
1.887 10 |
|
|
|
|||
130 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
