
Лабораторные работы / Лаба Метод модального формирования
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЁВА»
Институт ракетно-космической техники
Кафедра космического машиностроения
Методы баллистического и динамического проектирования
Отчет по лабораторной работе
«Метод модального формирования»
Работу выполнил студент группы 1512
Проверил:
Давыдов И.Е.
Самара 2020
МЕТОД МОДАЛЬНОГО ФОРМИРОВАНИЯ
Задача исследования динамической совместимости ГЧ с РКН рассматривается как задача выбора областей в пространстве проектных параметров, соответствующих устойчивости системы и заданному качеству переходных процессов в каналах управления, и формулируется как задача модального формирования на множестве спектров.
Пусть нам задана приведенная матрица
собственной динамики
 размерности
размерности
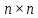 .
.
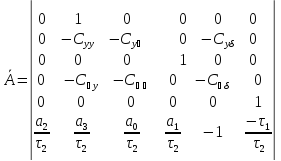
Численные коэффициенты:
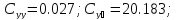
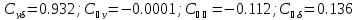
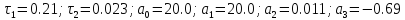
Введем данную матрицу в MathCad:
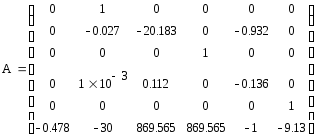
На множестве возможных значений проектных
параметров системы «РКН-ГЧ-АС» требуется
найти такую область
 (рисунок 1), которая соответствует
устойчивости системы и заданному
качеству переходных процессов системы
«РКН-ГЧ-АС», допустимых проектных
параметров задано совокупностью
неравенств вида
(рисунок 1), которая соответствует
устойчивости системы и заданному
качеству переходных процессов системы
«РКН-ГЧ-АС», допустимых проектных
параметров задано совокупностью
неравенств вида
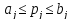 ,
,
где
 ,
,
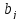 ,
,
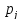 определяют заданные пределы изменения
параметров.
определяют заданные пределы изменения
параметров.

Рисунок 1 — Область
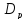 на плоскости проектных параметров
на плоскости проектных параметров
С другой стороны, заданному качеству
реакции системы на внешнее воздействие
соответствует определённая область
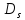 (рисунок 2) на плоскости комплексной
переменной
(рисунок 2) на плоскости комплексной
переменной
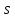 (
(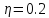 – степень быстродействия).
– степень быстродействия).

Рисунок 2 — Область
 на плоскости комплексной переменной
на плоскости комплексной переменной
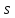
В качестве границы множества
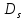 выбрана алгебраическая кривая четвёртого
порядка – овал Кассини, который описан
следующим уравнением
выбрана алгебраическая кривая четвёртого
порядка – овал Кассини, который описан
следующим уравнением
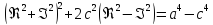 ,
,
где
 - ограничения области
- ограничения области
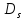 по действительной и мнимой осям
по действительной и мнимой осям
комплексной
плоскости
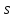 ,
соответственно;
,
соответственно;
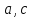 - параметры овала Кассини,
- параметры овала Кассини,
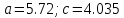 ;
;
знак
"+" перед
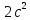 обозначает, что данный овал "вытянут"
относительно оси
обозначает, что данный овал "вытянут"
относительно оси
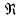 .
.
Построим этот овал Кассини (рисунок 3).
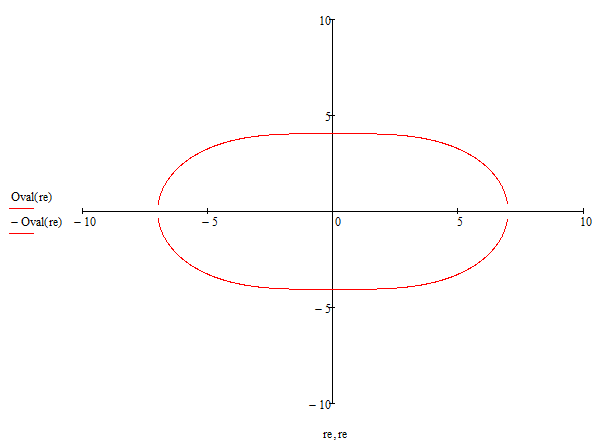
Рисунок 3 – Овал Кассини
При
помощи функции
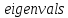 найдем собственные значения матрицы
найдем собственные значения матрицы
 :
:
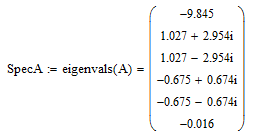
Чтобы
система была устойчива, необходимо,
чтобы все собственные значения матрицы
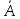 лежали внутри области
лежали внутри области
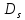 ,
то есть эти точки должны лежать внутри
овала Кассини (рисунок 4). Если хотя бы
одна из точек не лежит в пределах овала,
то система будет неустойчивой.
,
то есть эти точки должны лежать внутри
овала Кассини (рисунок 4). Если хотя бы
одна из точек не лежит в пределах овала,
то система будет неустойчивой.
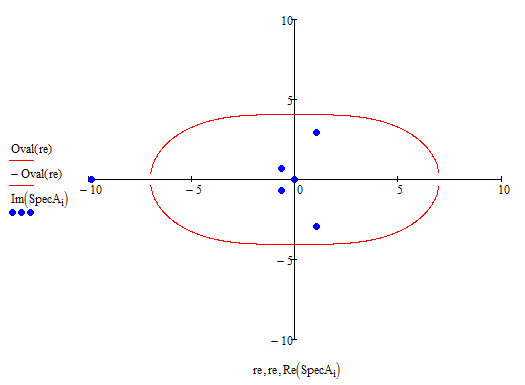
Рисунок 4 – Собственные значения матрицы
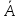 и овал Кассини
и овал Кассини
Как видно из рисунка 4, одна из точек лежит за пределами области, из чего можно сделать вывод о неустойчивости данной системы.
Зачастую в силу сложности конфигурации
множества
 ,
которое в проектных задачах может быть
произвольным, что вызывает определённые
трудности при получении функционала,
определяющего принадлежность спектра
полюсов данной области, поставим задачу
преобразования множества
,
которое в проектных задачах может быть
произвольным, что вызывает определённые
трудности при получении функционала,
определяющего принадлежность спектра
полюсов данной области, поставим задачу
преобразования множества
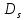 комплексной переменной s в некоторое
другое множество
комплексной переменной s в некоторое
другое множество
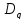 комплексной переменной
комплексной переменной
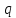 .
.
Для
простоты попытаемся привести область
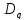 к окружности единичного радиуса. Для
этого введем матрице функциональных
преобразований
к окружности единичного радиуса. Для
этого введем матрице функциональных
преобразований
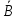 ,
которая получается из матрицы
,
которая получается из матрицы
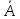 при помощи оператора
при помощи оператора
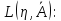

Тогда матрица
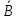 получится:
получится:
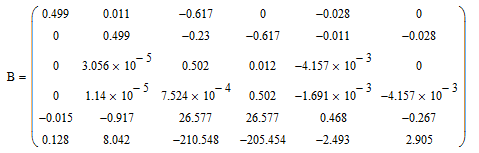
Отыщем собственные значения этой матрицы:
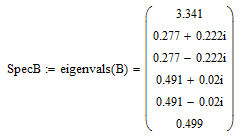
Отметим их на комплексной плоскости, чтобы убедиться, что все они попадают в окружность единичного радиуса (рисунок 5).
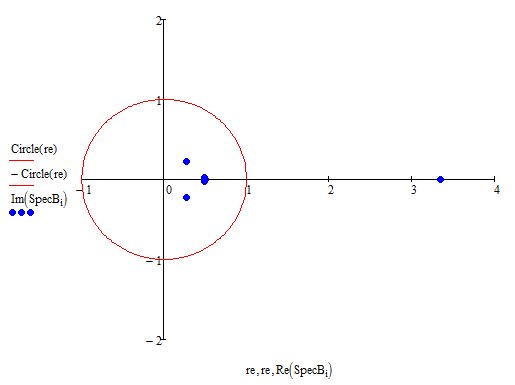
Рисунок 5 – Собственные значения матрицы
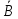 и
единичная окружность
и
единичная окружность
Как видно из рисунка 5, одна из точек не принадлежит единичной окружности, из чего можно сделать вывод, что система неустойчива.
Вывод: при использовании метода модального
формирования были найдены собственные
значения матрицы собственной динамики
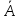 и
и
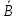 ,
а также построены области
,
а также построены области
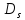 и
и
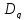 .
После анализа попадания собственных
значений данных матриц в соответствующие
области, было сделано заключение о
неустойчивости системы при исходных
параметрах.
.
После анализа попадания собственных
значений данных матриц в соответствующие
области, было сделано заключение о
неустойчивости системы при исходных
параметрах.
