Примеры решения домашних задач

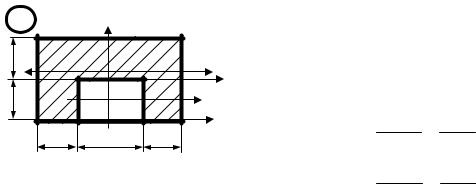
y1, y2, y, V, x0

1. Делим

сложное сечение на

простые и

1

определяем

площади

и

моменты

инерции

20

y0

x

составных элементов

относительно

собственных

центральных осей

20

x1

AI

b1 h1

7 4 28,0cм2 ;

x2

b1 h

3

7 43

I

1

4

20

30

20

U

J x1

12

12

37,33cм

;

Wxo=? Wyo=?

J

h1 b 3

4 7

3

114,33cм4 ;

I

1

y1

12

12

J

I

0.

x1 y 1

b2

h 3

3 2

3

AII

b

2

h

2

3 2 6,00cм 2 ; J II

2

2,00cм4 ;

x1

12

12

h1

b 3

2 3

3

J I

1

4,50cм4 ;

J

II

0.

x 2 y 2

y1

12

12

U c 0;

Vc

AI V I

AII V II

VcI

2,00cм;

28 2 6 1

cм.

c

c

2,2727

AI

AII

VcII

1,00cм.

28 6

AI J IIx2

AI

I

J x

J Ix

J IIx

J Ix1

b12

b12

b1

VcII

Vc

2

2,2727 0,2727cм;

28 2 1,2727 2

b1

Vc

Vc

1

2,2727 1,2727cм.

37,33 0,2727 2

6 27,70cм 4 ;

J

y

J I

J II

J I

J II

114,33 4,5

108,83cм 4 ;

J

x y

0.

y

y

y1

y

2

Следовательно,

центральные

оси

являются

главными

и

J x0 108,33cм4 ;

J y 0

27,7cм4 .

4. Определяем координаты наиболее удаленных от главных осей точек сечения.

Из рисунка видно, что

x0

наиб 3,50см;

y0

наиб

2,2727см.

5. Определяем главные моменты сопротивления сечения при изгибе

J x 0

108,33

3

Jy 0

27,7

3

Wx

30,95см

;

Wy

12,19см

.

y0

3,5

x0

0

наиб

0

наиб

2,2727

y, x0

y1

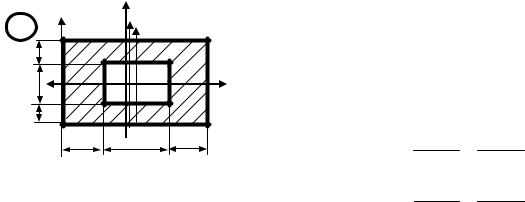
1.

Делим

сложное

сечение

на

2

простые

и

определяем

площади

и

V

y2

моменты

инерции

составных элементов

10

относительно собственных

центральных

20

y0

x1, x2, U, x

осей

AI

b1 h1 7,5 4 30,0cм 2 ;

10

25

30

20

b1

h 3

7,5 4

3

I

4

Wxo=? Wyo=?

J x1

12

40,00cм

;

12

J

h1

b 3

4 7,5

3

I

1

140,63cм4 ;

y1

12

12

J

I

0.

x1 y 1

b2

h 3

3 2

3

AII

b

2

h

2

3 2 6,00cм 2 ; J II

2

2,00cм4 ;

x1

12

12

h1

b 3

2 3

3

J I

1

4,50cм4 ;

J

II

0.

x 2 y 2

y1

12

12

AI U I AII

U II

U cI 3,75cм;

30 3,75 6 4

U c

c

c

3,6875 cм;

Vc 0.

AI AII

U cII 4,00cм.

30 6

J x J xI

JxII JxI

J IIx

40 2 38,00см4 ;

1

2

a1

I

U c

3,75 3,6875 0,0625cм;

J y J Iy

J IIy

J Iy1

2

2

U c

a1 AI J IIy 2 a1 AII

a1

II

U c

4 3,6875 0,3125cм.

30 2 0,31252 6 138,16c

U c

140,63 0,06252

м 4 ;

J x y

0.

Следовательно,

центральные

оси

являются

главными

и

J x0 138,16cм 4 ;

J y 0

38,00cм4 .

4. Определяем координаты наиболее удаленных от главных осей точек сечения.

Из рисунка видно, что

y0

наиб

7,5 3,6875 3,8125см;

x0

наиб

2,00см.

5. Определяем главные моменты сопротивления сечения при изгибе

Wx

J x 0

138,16

36,24см

3

Wy

Jy 0

38

19,00см

3

;

.

y0

x0

2

0

наиб

3,8125

0

наиб

y

y2

y0

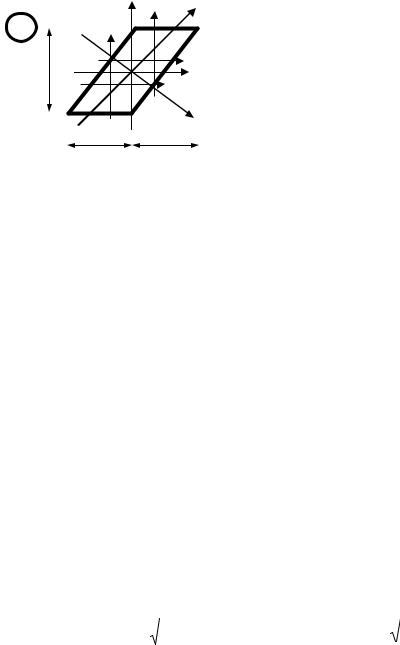
1.

Делим

сложное

сечение

на простые и

3

определяем площади и моменты инерции составных

I

элементов относительно собственных центральных

y1

x2

40

осей

x

1

1

x1

AI

АII

b

h

3 4 6,00cм 2 ;

II

x0

2

1

1

2

30

30

b1 h

3

3 4

3

J

I

J II

1

5,333cм4 ;

x1

x

2

36

36

h1 b 3

4 3

3

J

I

J II

1

3,00cм4 ;

y1

y

2

36

36

h12 b 2

4

2

3

2

J

I

J II

1

2,00см 4.

x1 y 1

x2 y

2

72

72

I

II

I

2

I

II

2

II

h1

h

1

h

1

4

J x

J x

Jx

Jx

b1

A

J x

b 2

A

b1 b2

0,6667cм .

2

3

6

1

2

6

2 5,333 0,6667 2 6 16,00см4 ;

J

J

I

J

II

J

I

a

2

A

I

J

II

a

2

A

I

a

a

b1

3

1,000cм .

y

y

y

y1

1

y

1

1

2

3

3

2

2 3 1,002 6 18,00cм4 ;

J x y

2 JxI

y

a1 b1 AI

2 2 1,0 0,6667 6 12,00cм 4 .

1

J x J y

1

16 18

1

J x

J y

2

2

16 18

2

2

J x0

, y 0

4 Jx y

4 12

17 12,04;

2

2

2

2

J

x 0

17

12,04 29,04cм4

;

J

y

17 12,04 4,96см 4 ;

0

tg

J x y

12

1,087;

0 47,39

.

J x J y 0

16 4,96

y0

y cos 0 x sin 0

2 cos 47,39 3 sin 47,39 3,68см.

II : x = 0; y = - 2,00 см;

x0

x cos 0 y sin 0 0 2 sin 47,39 1,47см.

5. Определяем главные моменты сопротивления сечения при изгибе

Wx

J x 0

29,04

7,89см

3

Wy

Jy 0

4,96

см

3

;

2,92

.

y0

x0

1,47

0

наиб

3,68

0

наиб