6.3.2. Кинематика планетарной передачи

В планетарных передачах одно из центральных колёс неподвижно, а степень подвижности равна единице. Если, например, в дифференциальной передаче, показанной на рис. 6.1, закрепить колесо 3, т.е. ω₃ = 0, то уравнение (6.1) приводится к формуле Виллиса для планетарных передач

,

(6.15)

или в общем виде

.

(6.16)

Эта формула справедлива для любой схемы планетарной передачи. Таким образом, передаточное отношение от любого колеса а передачи к водилу Н равно единице минус передаточное отношение этого же колеса а к неподвижному колесу в при остановленном водиле.

Рассмотрим применение формулы Виллиса к различным схемам планетарных передач, показанных в таблице 5.1.

Для схем I и II имеем

.

(6.17)

Для схемы III имеем

.

(6.18)

Для схем IV и V имеем

.

(6.19)

Передаточное отношение от центрального колеса 1 к сателлиту 2 можно определить по формуле

.

(6.20)

Зная связь с числами зубьев передачи, можно установить аналогичную связь при другом входном звене по следующим отношениям:

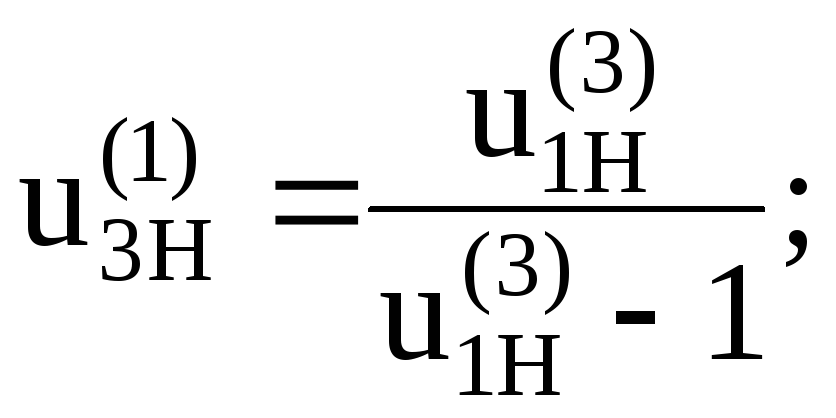
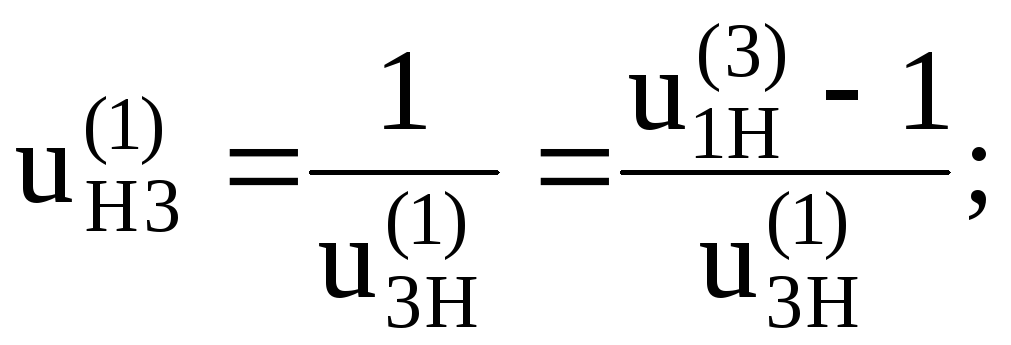
(6.21)

Пример 1. Определить передаточное отношение планетарной передачи по схеме III (табл.5.1), если

Решение:

.

Пример 2. Определить передаточное отношение планетарной передачи по схеме IV (табл.5.1), если z₁ = 100, z₂ = 99; = 100; z₃ = 101.

Решение:

Сначала определяем передаточное отношение по формуле Виллиса (6.15)

Тогда

Пример 3. Определить передаточное отношение сложного зубчатого механизма (рис. 6.11), если числа зубьев z₁ = 18, z₂ = 54; z₃ = 98, z₄ = 100; = 99; z₅ = 99.

Решение:

Данный механизм представляет собой двухступенчатую передачу, у которой ступень 1 – 2 является простой, а ступень Н – 5 планетарной двухрядной с внешним зацеплением.

Следовательно, где

Тогда

Так как 1, то данная передача является редуктором, а знак минус указывает на противоположное направление вращения зубчатых колёс 1 и 5.

Рис. 6.11. Схема сложного зубчатого механизма

6.3.3. Кинематика планетарной передачи типа3к

Для передачи типа 3К (рис. 6.4 а) составляются два выражения уравнения Виллиса

и

откуда исключением определяется передаточное отношение механизма при неподвижном центральном колесе 4.

(6.22)

Пример. Определить передаточное отношение планетарной передачи 3К (рис. 6.4 а), если = 18; = 36; = 33; = 87, = 90.

Решение:

Передаточное отношение передачи при неподвижном колесе 4 определяется по формуле (6.22)

Следовательно, передача является редуктором, в котором направление вращения зубчатых колёс 1 и 3 совпадают.

6.3.4. Кинематика замкнутых дифференциальных передач

Для замкнутых дифференциальных передач (рис. 6.5 в) необходимо дополнительно к уравнению Виллиса (6.1) составить уравнение связи между угловыми скоростями замыкаемых звеньев [5], [12]:

.

(6.23)

Решив его совместно с (6.1), получим

,

(6.24)

или в сокращённой записи

где .

(6.25)

В общем случае

,

(6.26)

где а, b и Н – центральные звенья дифференциальной ступени, а – входное звено, не связанное со звеном замыкания; d – выходное звено (может совпадать со звеном b или Н дифференциальной ступени).

Таким образом, передаточное отношение замкнутой дифференциальной передачи от звена а, не входящего в дополнительную связь со звеном замыкания, равно сумме двух передаточных отношений, каждое из которых определяется в предположении, что одно из центральных звеньев дифференциальной ступени условно остановлено, а мешающие вращению связи удалены.

Для передачи, изображенной на рис. 6.5 в

Следовательно,

(6.27)

При входном звене d, связанным со звеном замыкания или являющимся звеном замыкания, справедлива обратная формула

.

(6.28)

Если в замкнутом дифференциальном механизме имеется несколько контуров замыкания, то число слагаемых в формуле (6.25) всегда на единицу больше числа контуров.

Пример. Определить передаточное отношение редуктора двигателя вертолёта МИ – 6 (рис. 6.12), если = 31, = 68; = 31; = 29, = 89; = 48; = 29; = 106.

Рис. 6.12. Схема редуктора двигателя вертолёта МИ – 6

Решение. Редуктор представляет собой сложный зубчатый механизм, состоящий из простой конической передачи 1 – 2 и замкнутой дифференциальной передачи 2′ – Н(6). Следовательно, Передаточное отношение простой конической передачи равно Передаточное отношение замкнутой дифференциальной передачи определяется по формуле (6.26)

где

Тогда