6.3. Кинематика сателлитных передач

Для определения угловых скоростей или частоты вращения зубчатых колёс, а также передаточного отношения сателлитной передачи применяется метод обращения движения (метод Виллиса), который заключается в следующем: всем звеньям механизма условно сообщается дополнительная угловая скорость, обратная и численно равная угловой скорости водила H (–ω_н).

Тогда водило становится условно неподвижным, а сателлитная передача превратится в соосный простой механизм с неподвижными в пространстве осями вращения зубчатых колёс, называемый обращённым механизмом, (рис. 6.9 б).

Рис. 6.9. Схемы передач

а – дифференциальной двухрядной; б – обращенного механизма

6.3.1. Кинематика дифференциальной передачи

Рассмотрим применение метода Виллиса на примере двухрядной дифференциальной передачи (рис. 6.9 а).

Пусть ω₁, ω₂, ω₃ и ω_H – угловые скорости звеньев, а z₁, z₂, z_2′ и z₃ – числа зубьев рассматриваемой передачи. После применения метода Виллиса звенья обращённого механизма (рис. 6.9. б) будут иметь следующие угловые скорости (табл. 6.1)

Угловые скорости звеньев

Таблица 6.1

Звенья механизма	Действительные угловые скорости звеньев	Угловые скорости звеньев обращённого механизма
1	ω1	ω1–ωH
2	ω2	ω2 – ωH
3	ω3	ω3 – ωH
H	ωн	ωH – ωH = 0

Тогда передаточное отношение будет равно:

.

(6.1)

Зависимость (6.1) называется уравнением Виллиса для дифференциальной передачи.

С другой стороны обращённый механизм представляет собой двухступенчатую простую передачу, для которой

.

(6.2)

Следовательно,

.

Определим степень подвижности дифференциального механизма, представленного на рис. 6.9 а

, где ; ; .

Тогда .

В данном механизме должно быть два входных звена. Задаваясь двумя угловыми скоростями и зная числа зубьев передачи, можно определить угловую скорость выходного звена. Угловую скорость сателлита 2 можно определить по формуле:

=.

(6.3)

Пример. Определить частоту вращения водила механизма (рис. 6.9 а), если известны 1/c, 1/c (вращение колеса 3 противоположно вращению колеса 1), z₁=30; z₂=60; =20; z₃ =110.

Решение:

1. Определим по формуле (6.2) передаточное отношение обращённого механизма

.

2. Решаем уравнение (6.1) относительно:

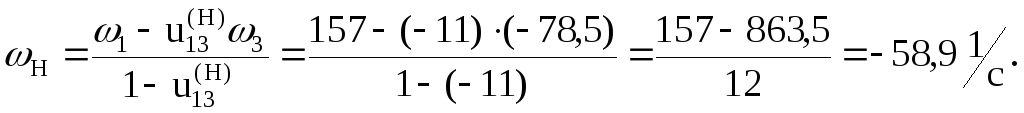
3. Определяем частоту вращения водила

.

Знак “минус” указывает, что вращение водила также противоположно вращению звена 1.

Для дифференциальных передач с несколькими степенями свободы удобно пользоваться формулами, полученными в результате дифференцирования зависимости угла поворота выходного элемента от углов поворота входных звеньев, [9].

Рассмотрим, например, дифференциальную передачу, показанную на (рис. 6.10).

Степень свободы такой передачи равна

.

Следовательно, передача должна иметь три входных звена. Предположим, что входными являются 1,3 и 6 звенья. Тогда угол поворота водила H₂ является функцией углов поворота колес 4 и 6. Но угол поворота колеса 4 в свою очередь, зависит от углов поворота колес 1 и 3.

Рис. 6.10. Схема дифференциальной передачи с тремя степенями свободы

Таким образом:

,

,

(6.4)

(6.5)

.

(6.6)

Дифференцируя (6.6) по времени, получим:

.

(6.7)

Рассмотрим частные случаи, когда два из трёх входных звеньев остановлены,

при

,

(6.8)

при

,

(6.9)

при

,

(6.10)

Подставляя значения частных производных в уравнение (6.7), получим:

.

(6.11)

Последовательное соединение дифференциальных механизмов обладает свойством, при котором сумма коэффициентов при угловых скоростях входных звеньев равна единице, т.е.

.

(6.12)

Аналогично можно получить зависимость частот вращения звеньев дифференциального механизма, степень подвижности которого (рис 6.1)

(6.13)

Причем

(6.14)