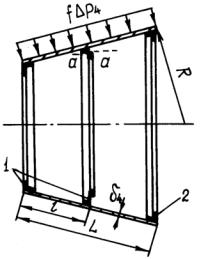
1.7. Стабилизирующая юбка

Стабилизирующая юбка предназначена для придания неуправляемому головному отсеку статической устойчивости на участке свободного полета в плотных слоях атмосферы. Конструкция ее обычно представляет собой тонкую коническую оболочку, подкрепляемую изнутри шпангоутами (рис. 13). Наружная поверхность стабилизирующей юбки покрывается слоем, защищающим металлическую оболочку от аэродинамического нагрева. Этот слой теплозащиты при большой толщине увеличивает жесткость оболочки. Однако в действительности теплозащитное покрытие не воспринимает внешнее давление из-за газовой проницаемости материала, из которого оно изготовлено.

Подкрепляющее влияние теплозащиты невозможно использо-

Рис. 13. Стабилизирующая юбка ГО вать также из-за отсутствия

плотного соединения теплозащиты и силовой оболочки корпуса на всей поверхности конструкции и низкого модуля упругости по сравнению с материалом силовой стенки. Угол полураствора конической оболочки, выполняющей функции стабилизирующей юбки, не превышает 20°, поэтому ее можно относить к слабоконическим оболочкам, расчет которых проводится по формулам цилиндрических оболочек. Следовательно, задача сводится к расчету цилиндрической оболочки, подкрепленной изнутри промежуточными шпангоутами 1 и имеющей один жестко заделанный, а другой свободный край. Оболочка при этом нагружена внешним давлением. Наличие свободного края и составляет основную особенность при расчете стабилизирующей юбки.

Анализ влияния граничных условий на свободном крае оболочки, проведенный с помощью полубезмоментной теории оболочек [3], показывает, что если жесткость торцевого шпангоута 2, установленного на краю оболочки, превышает некоторое значе-

28

ние, то он может считаться жестко заделанным. Для оболочек средней длины эта жесткость определяется по формуле

где D – цилиндрическая жесткость оболочки; L – длина ее вдоль образующей; IT – момент инерции сечения шпангоута. Далее будем рассматривать стабилизирующую юбку как эквивалентную ей цилиндрическую оболочку длиной L и радиусом R, равным второму главному радиусу кривизны у ее основания. Если оболочка, кроме торцевого, имеет еще и промежуточные шпангоуты, то ее можно представить в виде конструктивно-ортотропной оболочки, жестко заделанной по ее краям. Такая оболочка при нагружении ее внешним давлением работает на прочность, а также на общую и местную устойчивость. Тангенциальное напряжение по безмоментной теории σ2 = pp Rδ4 ,(σ2 < 0), где pp = f p4 –

расчетное давление; f – коэффициент безопасности; δ4 – толщина стенки.

Меридиональные напряжения в этом случае растягивающие (см. рис. 10) и определяются по формуле: σ1 = Np 2πRδ4 ,

(σ1 > 0) где Np – расчетная осевая сила. Так как напряжения раз-

ных знаков, то эквивалентные напряжения по III теории прочности равны:

Критическое давление общей потери устойчивости ортотропной оболочки, жестко заделанной по краям, определяется по формуле

где B1 = Eδ4 – жесткость на растяжение в осевом направлении; D2 = D + EIi l – жесткость подкрепленной оболочки в тан-

генциальном направлении; D = Eδ34 12(1−μ2 ) – цилиндри-

ческая жесткость; Ii – центральный момент инерции сечения шпангоута относительно оси, параллельной образующей оболочке.

29

Для участка обшивки между шпангоутами критическое давление местной потери устойчивости определяется по формуле П.Ф. Папковича:

где l – расстояние между шпангоутами.

В формулы (1.37) и (1.38) входят жесткость промежуточных шпангоутов и расстояние между ними, которые зависят от формы их сечения, поэтому проектировочный расчет подкрепленной оболочки необходимо рассматривать для конкретного вида подкрепления.

1.7.1. Проектировочный расчет

Установим условие, при котором гладкую оболочку необходимо «подкреплять» шпангоутами, и с этой целью найдем сначала давление, при котором толщина гладкой оболочки, определенная из условия устойчивости и прочности, будет одинаковой. Приравняв эквивалентное напряжение пределу текучести σ0.2, получим

30

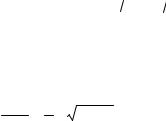
Уравнение легко решается относительно pp σ0,2 при Np = 0 , т.е. когда осевая сила отсутствует. В этом случае искомое давление

Уравнение (1.41) можно свести к иррациональному, если степень 0,4 в сомножителе с давлением заменить на 0,5:

Подставляя полученное значение в любую из формул (1.39) или (1.40), находим искомую толщину δ4 / L . Таким образом, если толщина гладкой оболочки, определяемая из условия прочности, больше, чем δ4 / L , т.е. внешнее давление больше

граничного, то несущая способность определяется ее устойчивостью.

Далее, на основании рекомендаций [18], оболочку, работающую на устойчивость от внешнего давления, целесообразно подкрепить промежуточными шпангоутами, если выполнено условие

Теперь для определения толщины оболочки, расстояния между шпангоутами, размеров его сечения необходимо воспользоваться следующими условиями:

1) местной устойчивости оболочки между шпангоутами:

Формулу (1.37) в данном случае удобнее переписать в виде

31

3) общей устойчивости шпангоута как кольца, сжатого внешней погонной нагрузкой:

4) местной устойчивости элементов шпангоута:

σмкр ≥ σ1 .

Критические напряжения местной устойчивости элементов профиля шпангоута, рассматриваемых как бесконечно длинные пластинки, сжатые по короткой стороне, определяются по формуле

σмкр = 0,9kE(hb)2 ,

где k=4 – для стенки и стойки; k =0,425– для полки; h – толщина

одинаковых толщинах полки и стенки шпангоута отношение (hп bc )= 0,325 . В табл. 1 приводятся типичные значения b/h для

различных материалов.

Т а б л и ц а 1

Материал E , Мпа σ0,2, Мпа E/σ0,2 (b/h)c (b/h)п

32

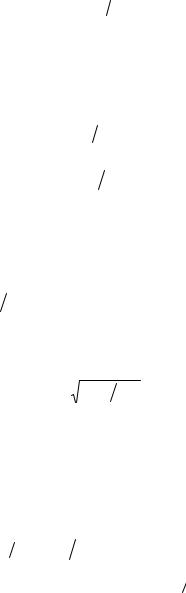
где из уравнения равновесия четверти кольца можно получить

Основные этапы проектировочного расчета оболочки, подкрепленной шпангоутами, можно представить следующим образом. Сначала устанавливается причина разрушения шпангоута (прочность или устойчивость) и с этой целью определяется граничная погонная нагрузка. Из условия прочности (1.46) с учетом (1.47) площадь сечения шпангоута

а из условия его общей устойчивости (1.45)

Но момент инерции шпангоута можно выразить через его площадь по формуле

где ki – коэффициент формы шпангоута.

Ii = Ab4 /12 , а k=1/(12A).

Если воспользоваться табл. 1, то k = (0,5-1) для пластинки со свободным краем. Тогда с учетом (1.50) из (1.49) получим

а приравняв (1.48) к (1.51), найдем граничную погонную нагрузку:

Если qi ≤ qi0 , то шпангоут работает на устойчивость. Рассматривая случай работы шпангоута на устойчивость, на-

33